Собственные векторы симметрической матрицы

Ниже будет доказано, что в пространстве имеется ортонормированный базис, состоящий из собственных векторов симметрического преобразования. Сначала докажем следующие леммы.

Лемма 1. Даны две матрицы и порядка n

где и – матрицы порядка . Тогда справедливы следующие утверждения:

1.

2 . Если матрица обратима и , то матрица обратима и

3.

Доказательство

1. Найдем первую строку и первый столбец матрицы

Теперь найдем элемент матрицы , расположенный в -й строке и -м столбце, ,

^.

2. Используя доказанное выше первое утверждение леммы, имеем

=

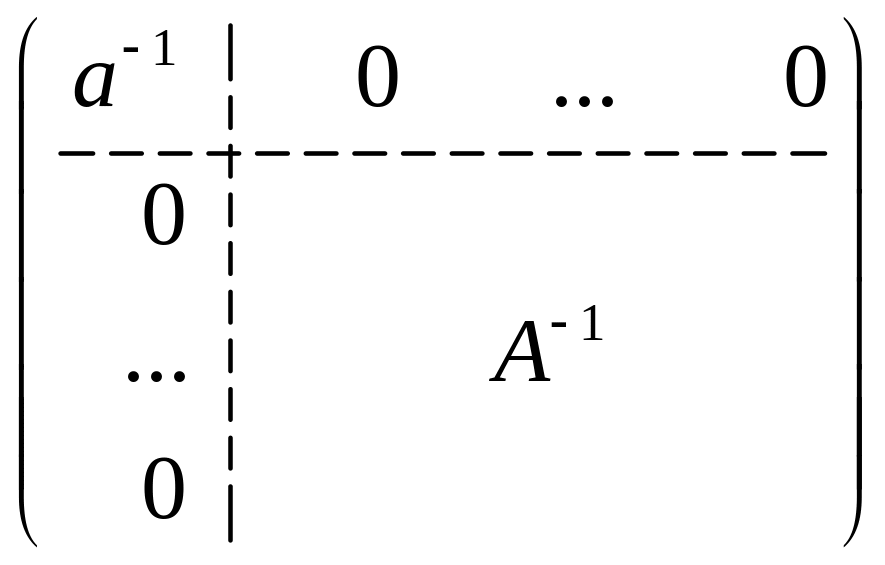3. , . ■

□ Лемма 2. Если – ортогональная матрица порядка , то

− ортогональная матрица порядка n.

Доказательство. Из ортогональности матрицы следует, что (теорема 1.16). Ортогональность матрицы будет вытекать из равенства , которое установим, используя лемму 1

■

Построение ортонормированного базиса , состоящего из собственных векторов симметрической матрицы, будет основываться на следующей теореме.

□ Теорема 3.21. Каждую симметрическую матрицу можно при помощи ортогональной матрицы привести к диагональному виду

.

Доказательство проведем методом математической индукции по порядку матрицы . Если матрица имеет порядок, равный единице, т. е. , то она уже является диагональной. Далее, единичная матрица первого порядка, т. е. , обратима и обратная матрица имеет вид . Обе эти матрицы являются ортогональными. Наконец, из матричного равенства следует, что .

Пусть теперь утверждение теоремы справедливо для всех симметрических матриц, порядок которых равен . Докажем теорему для симметрической матрицы порядка . Из теоремы 3.20 следует, что матрица имеет собственное значение . Возьмем в подпространстве ненулевой вектор и нормируем его. Полученный вектор обозначим символом . Так как , то . Дополним нормированный вектор до ортонормированного базиса пространства и рассмотрим ортогональную матрицу , столбцами которой являются координаты векторов этого ортонормированного базиса. Теперь для первого столбца матрицы получим следующее выражение:

.

Отсюда следует, что матрица может быть записана в виде

Так как матрица симметрическая (теорема 3.19), то все элементы этой матрицы, расположенные в первой строке, за исключением быть может , равны нулю. Итак

Из леммы 1 вытекает, что

Из симметричности матрицы вытекает равенство . Отсюда следует, что и, значит, симметрическая матрица.

Симметрическая матрица имеет порядок и, по предположению индукции, найдется такая ортогональная матрица , что

.

Из леммы 2 следует ортогональность матрицы

,

а из леммы 1 вытекает, что матрица обратима и

Теперь обозначим произведение ортогональных матриц и символом , т. е. . Из теоремы 3.17 следует, что – ортогональная матрица. Используя лемму 1, получим следующую цепочку равенств:

= =

т. е. ортогональная матрица приводит матрицу к диагональному виду. ■

Теперь доказанная теорема 3.21 позволяет построить в пространстве Rⁿ ортонормированный базис, состоящий из собственных векторов симметрического преобразования .

□ Теорема 3.22. Пусть все различные собственные значения симметрической матрицы _. Тогда объединение ортонормированных базисов подпространств является ортонормированным базисом пространства .

Доказательство. В каждом подпространстве выберем ортонормированный базис. Из теорем 3.21 и 3.11 следует, что объединенная система этих базисов является базисом Rⁿ. В силу построения векторы нормированы. Докажем ортогональность этой системы векторов.

Пусть и – произвольные различные векторы системы . Если они лежат в одном подпространстве то они принадлежат ортонормированному базису этого подпространства и, значит, ортогональны. Пусть теперь и . Тогда

, .

Отсюда следует ,

Из симметричности матрицы вытекает равенство левых частей этих равенств и, значит, равны их правые части

.

Так как собственные значения и различны, то и, значит, ■

Алгоритм построения ортонормированного базиса пространства , состоящего из собственных векторов симметрической матрицы .

1. Найти собственные значения матрицы .

2. Для каждого собственного значения найти фундаментальный набор решений системы уравнений , т. е. найти базис подпространства .

3. Ортогонализировать и нормировать найденные базисы под-пространств.

4. Объединить ортонормированные базисы подпространств .

Пример

Найти ортонормированный базис пространства состоящий из собственных векторов матрицы

Решение. Сначала найдем характеристический многочлен матрицы

Собственные значения матрицы равны 2, 2 и 4.

Теперь надо найти базисы подпространств , и , т. е. найти фундаментальные наборы решений систем уравнений: , и Базис подпространства состоит из одного вектора , базис A(2) образуют векторы , и базис подпространства состоит из одного вектора .

Базис подпространства не является ортогональным. После его ортогонализации и объединения базисов всех подпространств получим ортонормированный базис пространства , состоящий из собственных векторов матрицы : .

Задачи

1. Доказать, что для любой матрицы матрица – симметрическая матрица.

2. Доказать, что для любой обратимой матрицы матрица будет симметрической тогда и только тогда, когда симметрической будет матрица .

3. Доказать, что если и − симметрические матрицы, то матрицы и также симметрические.

4. Доказать, что симметрические матрицы и перестановочны тогда и только тогда, когда симметрическая матрица.

5. Доказать, что матрица cимметрическая, если матрица ортогональная и = Е.

6. Доказать, что матрица симметрическая, если в пространстве имеется ортонормированный базис, состоящий из собственных векторов матрицы .

Найти ортонормированный базис пространства R , состоящий из собственных векторов симметрической матрицы.

7. 8. 9.

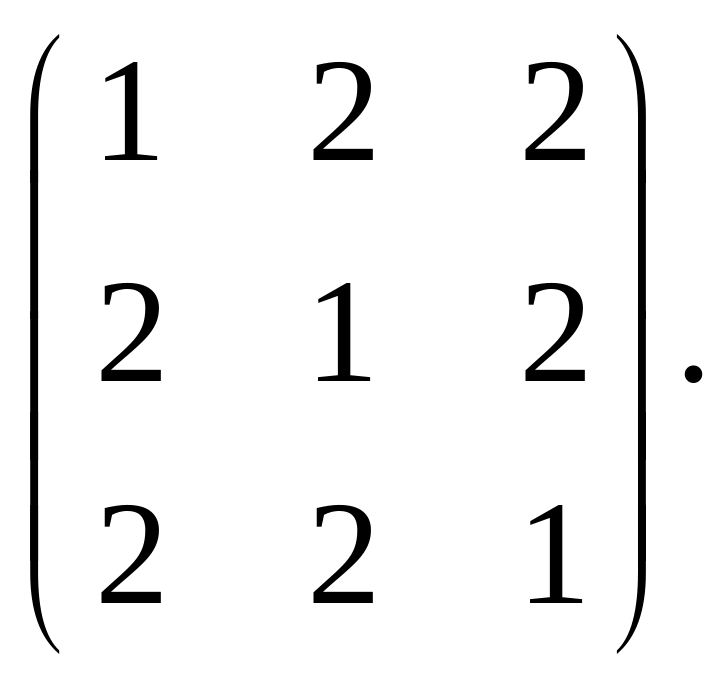
Найти ортогональную матрицу, которая приводит симметрическую матрицу к диагональному виду, написать этот диагональный вид.

10. 11. 12.

13. Найти все диагональные матрицы, к которым приводится при помощи ортогональной матрицы симметрическая матрица

.

106