3.6. Базис пространства , состоящий из собственных векторов матрицы

Пусть все различные собственные значения матрицы . Выберем базис в каждом подпространстве . Объединяя эти базисы, получим линейно независимую систему векторов, состоящую из собственных векторов матрицы (п. 3.5, свойство 2). Существует ли базис пространства , состоящий из собственных векторов матрицы? В общем случае ответ отрицательный, потому что матрица может не иметь собственных значений и, значит, собственных векторов.

□ Теорема 3.11. Дана матрица A. Равносильны следующие условия:

1. В пространстве имеется базис, состоящий из собственных векторов матрицы .

2. Объединение базисов подпространств является базисом пространства где все различные собственные значения матрицы

3. Можно построить такую обратимую матрицу T, что

Доказательство

1) 2). Пусть ,…, – базис пространства , состоящий из собственных векторов матрицы . Обозначим через ,…, объединение базисов подпространств Из свойства 2 в п. 3.5 следует линейная независимость системы векторов

Если вектор принадлежит подпространству , то вектор разлагается по базису подпространства , который является частью системы и, значит, каждый вектор системы разлагается по системе векторов . Отсюда и из условия: – базис следует, что каждый вектор из подпространства , разлагается по системе векторов . Следовательно, система векторов – базис пространства .

2) 3). Так как объединение базисов подпространств является базисом пространства то оно содержит n векторов, которые обозначим через . Вектор принадлежит одному из подпространств , т. е. , где одно из чисел .

Рассмотрим матрицу , столбцами которой являются векторы . Так как векторы образуют базис пространства Rⁿ, то матрица обратимая. Теперь справедливость утверждения 2) 3) вытекает из следующей цепочки импликаций:

3) 1). Пусть . Матрица по условию обратима и, значит, система ее столбцов линейно независимая и состоит из векторов. Следовательно, они образуют базис пространства Rⁿ. Остается доказать, что базис состоит из собственных векторов матрицы . Это утверждение вытекает из следующей цепочки импликаций:

т. е. собственный вектор матрицы , принадлежащий ее собственному значению .■

Матрица приводит матрицу к диагональному виду, если существует такая обратимая матрица , что

.

Пример

Выяснить, приводится ли матрица к диагональному виду. Найти матрицу , приводящую матрицу к диагональному виду, и найти диагональный вид.

.

Решение. Найдем собственные значения матрицы

Собственные значения матрицы равны , , .

Базис каждого из подпространств , , состоит из одного вектора, соответственно , , .

Матрица

,

столбцами которой являются координаты векторов , приводит матрицу к диагональной матрице

,

на главной диагонали которой находятся собственные значения матрицы , причем .

Задачи

1. Матрица приводит матрицу к диагональному виду. Найти собственные значения матрицы , не решая уравнение =0.

2. Построить алгоритм, который позволяет выяснить, приводит ли матрица матрицу к диагональному виду, и не требует решения уравнения =0.

3. Выяснить, приводит ли матрица матрицу к диагональной матрице и если приводит, то найти ее, не вычисляя матрицу

а) =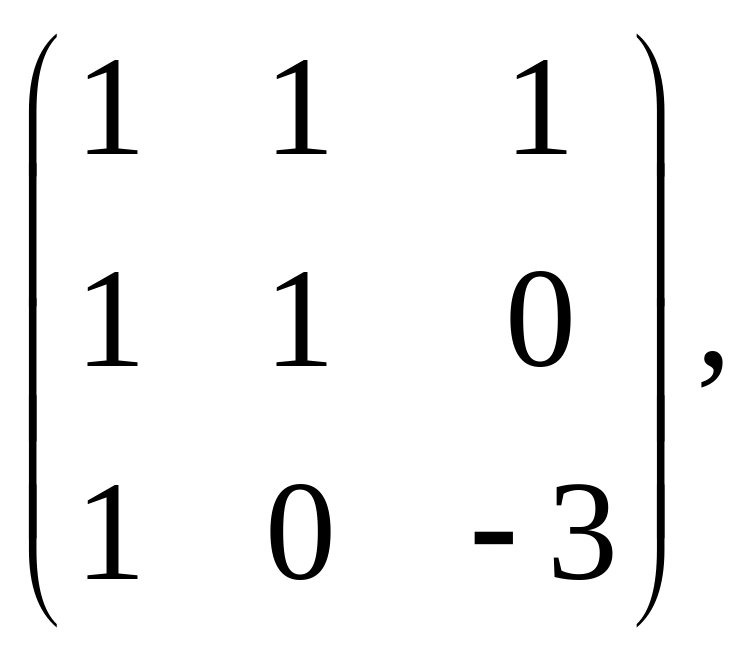 = б)

4. Найти базис пространства Rⁿ, состоящий из собственных векторов матрицы

a) 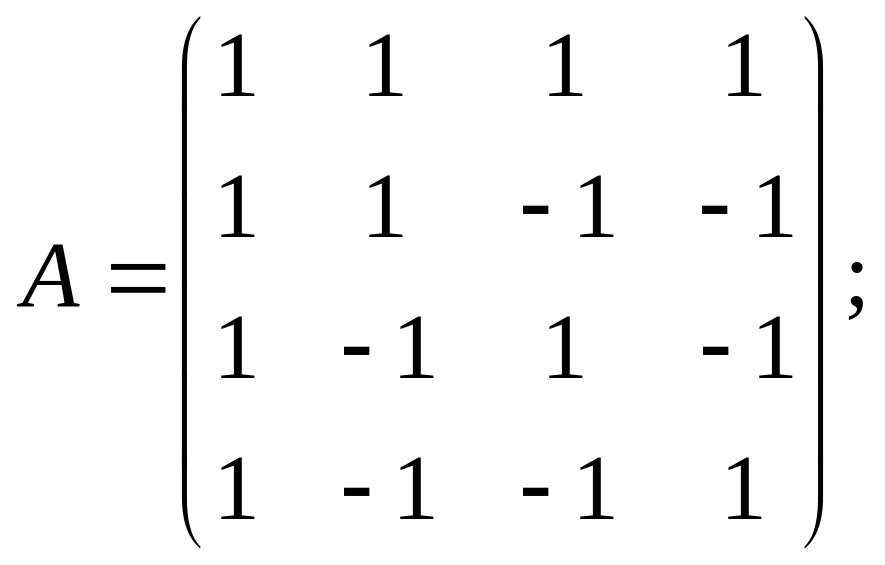б)