2.7. Прямые гиперплоскости и полупространства

в пространстве

В этом параграфе рассматриваются наиболее важные для приложений множества: прямые, гиперплоскости и полупространства.

1. Прямые в пространстве

Прямой в пространстве называется аффинное множество, размерность которого равна единице.

Ненулевой вектор , параллельный прямой , называется ее направляющим вектором. Направляющий вектор прямой принадлежит подпространству . Это подпространство одномерно и направляющий вектор является его базисом. Отсюда следует, что каждые два направляющих вектора прямой пропорциональны.

□Теорема 2.17. Справедливы следующие утверждения.

1) Уравнение

является уравнением прямой тогда и только тогда, когда прямая проходит через точку параллельно ненулевому вектору .

2) Система уравнений

является уравнением прямой тогда и только тогда, когда прямая проходит через точку перпендикулярно линейно независимым векторам .

Доказательство следует из теорем 2.15 и 2.16, в формулировке которых .■

□Следствие. Множество решений уравнения , является прямой, проходящей через точку параллельно вектору .

Доказательство. Из условия следствия вытекает , а из теоремы 2.13 следует , и, значит, прямая. Теперь утверждение следствия вытекает из необходимости теоремы 2.17.■

Через каждые две точки в пространствах и можно провести только одну прямую. Этот утверждение справедливо и в пространстве .

□ Теорема 2.18. Пусть и различные точки пространства . Тогда совокупность всех таких точек пространства , для которых является единственной прямой в пространстве , проходящей через точки и .

Доказательство. Из условия теоремы следует:

т.е. прямая, проходящая через точку параллельно вектору и

Рассмотрим произвольную прямую в пространстве , проходящую через точки и , т.е. . Тогда и так как размерность равна 1, то .

Итак, множества и имеют общую точку и их направляющие подпространства совпадают. Из теоремы 2.9 вытекает совпадение множеств и .■

Множество точек называется отрезком в пространстве . Отрезок содержит точки и : точку получаем, при значении , а точку – при значении . Точки и называются концами отрезка . Точка , принадлежащая отрезку и не совпадающая с его концами, называется внутренней точкой этого отрезка. Очевидно, что отрезок является подмножеством прямой, проходящей через точки и .

В пространстве прямая и плоскость либо не имеют общих точек, либо имеют одну общую точку, либо все точки прямой принадлежат плоскости. Обобщением этого утверждения является нижеследующая теорема.

□ Теорема 2.19. Прямая и аффинное множество в пространстве либо не имеют общих точек, либо имеют одну общую точку, либо все точки прямой принадлежат аффинному множеству.

Доказательство. Зададим прямую параметрическим уравнением , а аффинное множество – системой линейных уравнений . Общие точки прямой и аффинного множества являются решениями системы

Эта система уравнений имеет столько решений, сколько их имеет уравнение

или уравнение

. (7)

Возможны два случая: 1) и 2) .

В первом случае уравнение (7) имеет единственное решение, если векторы и пропорциональны, и не имеет решения в противном случае.

Во втором случае уравнение (7) не имеет решений, если . Если же , то уравнение (7) имеет решение при любом значении

Итак, уравнение (7) или не имеет ни одного решения, или имеет одно решение, или имеет решение при любом значении . Отсюда следует утверждение теоремы.■

Примеры

1. Даны координаты точек: Выяснить, пересекаются ли отрезки и

Решение. Напишем уравнения отрезков и :

Эти отрезки имеют общую точку тогда и только тогда, когда имеет решение система уравнений:

(8) Так как координаты векторов

то уравнение системы (8) в координатной форме имеет вид:

Решением этой системы уравнений являются числа: Так как значение не принадлежит , то отрезки и не пересекаются.

2. Аффинное множество задано системой линейных уравнений

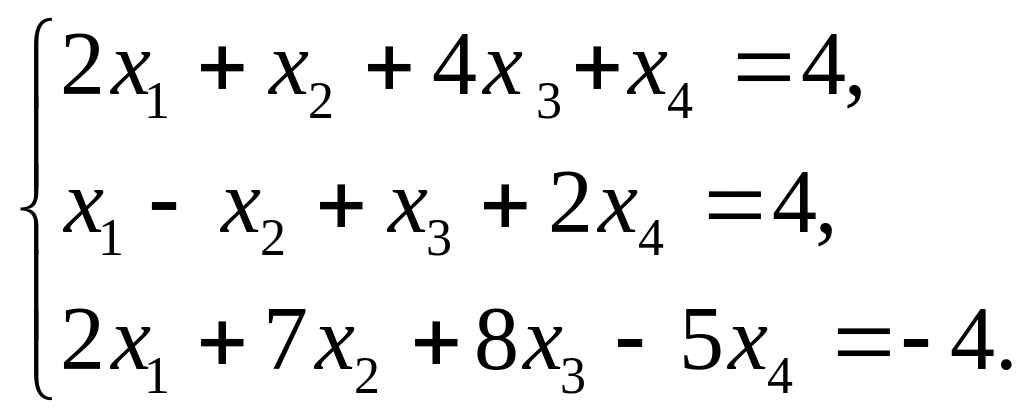
Написать уравнение прямой, не имеющей общих точек с множеством

Решение. Как следует из теоремы 2.19, прямая не имеет общих точек с аффинным множеством если, во-первых, т.е. вектор является решением уравнения , и, во-вторых, т.е. точка не является решением уравнения .

Вектор решение уравнения а точка не является решением уравнения . Следовательно, прямая или

не имеет общих точек с множеством ●

Задачи

1. Доказать, что две пересекающиеся прямые в пространстве содержатся в двумерном аффинном множестве.

2. Доказать, что две прямые в пространстве , направляющие векторы которых пропорциональны, содержатся в двумерном аффинном множестве.

3. Доказать, что наименьшее аффинное множество, содержащее две прямые, которые не пересекаются и направляющие векторы которых не пропорциональны, имеет размерность больше двух.

4. Прямая и аффинное множество имеют две общие точки. Будет ли прямая принадлежать аффинному множеству?

5. Доказать, что множество в пространстве будет аффинным, если оно содержит каждую прямую, проходящую через две различные точки из множества .

6. Даны параметрические уравнения прямых:

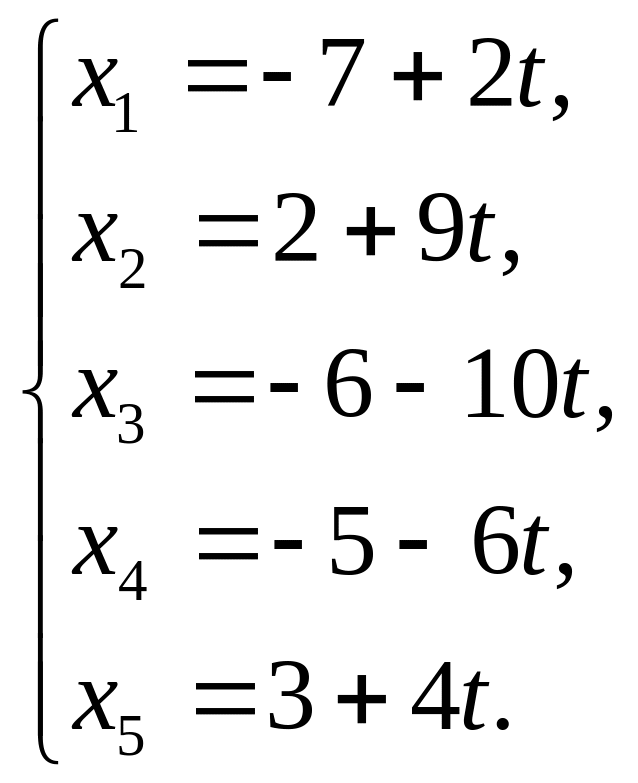
Построить аффинное множество наименьшей размерности, содержащее эти прямые.

7. Задать две прямые, которые не содержатся в двумерном аффинном множестве.

8. Прямая и аффинное множество имеют общую точку. Направляющий вектор прямой принадлежит подпространству L . Доказать, что прямая содержится в аффинном множестве

9. Прямая содержит точку, которая не принадлежит аффинному множеству . Будет ли прямая иметь общие точки с аффинным множеством, если направляющий вектор прямой не принадлежит направляющему подпространству L ?

10. Найти параметрическое уравнение прямой, принадлежащей аффинному множеству, заданному уравнением