
- •Глава II. Аффинные множества
- •2.2. Аффинные множества
- •2.3. Задание аффинных множеств
- •1. Задание аффинного множества системой линейных уравнений
- •3. Задание аффинного множества
- •2.4. Направляющее подпространство
- •□ Теорема 2.7. Если – аффинное множество в пространстве , то множество является подпространством пространства .
- •1. Направляющее подпространство множества
- •2. Направляющее подпространство аффинной оболочки
- •3. Направляющее подпространство
- •2.5. Размерность аффинного множества
- •2.6. Уравнения аффинного множества
- •1. Уравнение фигуры
- •2. Параметрическое уравнение аффинного множества
- •2. Общее уравнение аффинного множества в пространстве
- •2.7. Прямые гиперплоскости и полупространства
- •1. Прямые в пространстве
- •2. Гиперплоскости в пространстве
- •3. Полупространства пространства
- •2.8.Прямые, плоскости и полупространства в
- •2. Общее уравнение прямой в пространствах и
- •3. Полупространства в пространствах и
2.4. Направляющее подпространство
Пусть
– подмножество точек пространства![]() Вектор
Вектор
![]() называется
параллельным
множеству
,
если найдется такая пара точек
называется
параллельным
множеству
,
если найдется такая пара точек
![]() из множества
,
что
из множества
,
что
![]() .
Из
этого
определения
следует, что вектор
,
где
и
–
точки из множества
,
параллелен
.
Множество всех векторов пространства
,
которые параллельны множеству
,
обозначим символом
.
Из
этого
определения
следует, что вектор
,
где
и
–
точки из множества
,
параллелен
.
Множество всех векторов пространства
,
которые параллельны множеству
,
обозначим символом
![]() .
.
□ Лемма (о параллельном векторе).
Если
вектор
,
параллельный аффинному множеству
,
отложить от некоторой точки C
множества
:
![]() ,
то конец D
этого вектора также принадлежит
,
т.е.
,
то конец D
этого вектора также принадлежит
,
т.е.
![]() ,
,
C
D
,
,
C
D
![]()
Доказательство. Так как вектор параллелен множеству , то найдутся такие точки М, N из множества , что . Теперь имеем
![]() .
.
Из
леммы §2.2 следует, что точка
![]() принадлежит множеству
.
■
принадлежит множеству
.
■
Следствие. Если точка принадлежит аффинному множеству , то справедливы следующие утверждения:
1)
вектор
![]()
![]()
![]() ,
;
,
;
2)
точка
![]()
Доказательство.
1) Необходимость. Дано, что вектор . Отложим его от точки множества : . Из леммы о параллельном векторе следует N .
Достаточность.
Вектор
,
.
Так как точка
принадлежит множеству
,
то, вектор
![]() параллелен множеству
параллелен множеству
![]() т.е.
.
т.е.
.
2)
Необходимость. Из
условия следует, что оба конца вектора
принадлежат множеству
,
а поэтому
![]()
Достаточность.
Дано,
что вектор
![]() ,
т.е. вектор
параллелен множеству
и
отложен от точки
этого множества. Из леммы о параллельном
векторе следует
,
т.е. вектор
параллелен множеству
и
отложен от точки
этого множества. Из леммы о параллельном
векторе следует
![]() ■
■
□ Теорема 2.7. Если – аффинное множество в пространстве , то множество является подпространством пространства .
Доказательство. Для доказательства теоремы достаточно установить справедливость следующих двух утверждений:
если
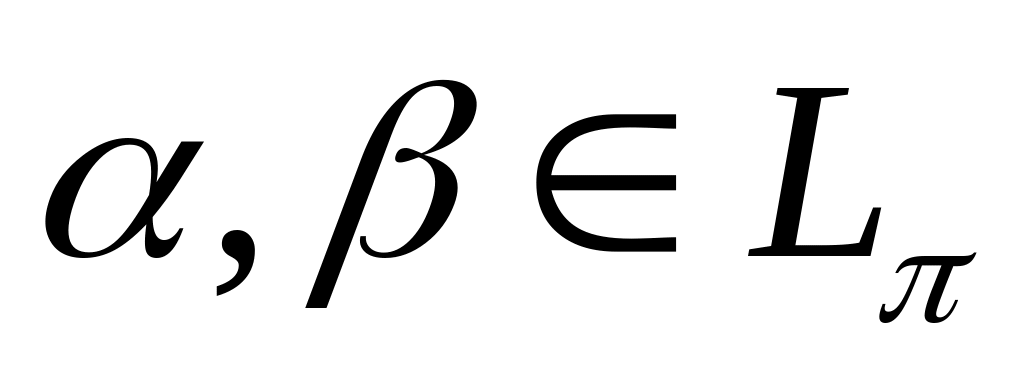 ,
то
,
то
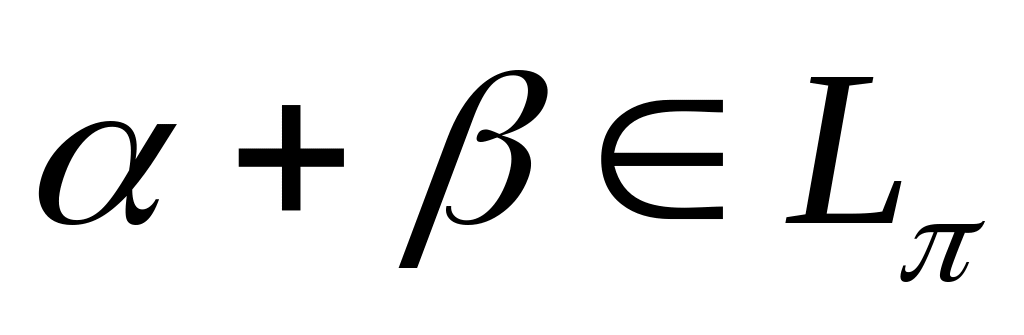 ;
;если
 ,
то
,
то
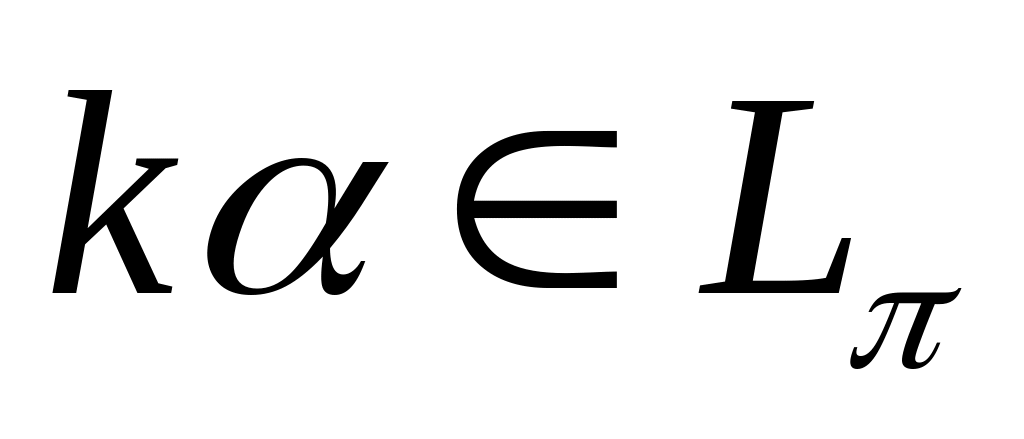 при любом
при любом
 .
.
1)
Рассмотрим два произвольных вектора
![]() из множества
.
Отложим их от некоторой точки
:
из множества
.
Отложим их от некоторой точки
:
![]() .
Из леммы о параллельном векторе следует,
что точки
и
принадлежат множеству
.
Отложим вектор
.
Из леммы о параллельном векторе следует,
что точки
и
принадлежат множеству
.
Отложим вектор
![]() от той же точки М,
и пусть
от той же точки М,
и пусть
![]() .
Покажем, что точка
принадлежит множеству
.
Из равенств
.
Покажем, что точка
принадлежит множеству
.
Из равенств
![]()
![]() и
следует
и
следует
![]() =
=![]() −
−
![]() =
=
![]() +
+![]() −
.
−
.
Теперь из леммы §2.2 вытекает, что точка принадлежит аффинному множеству . Итак, и точки и принадлежат аффинному множеству . Следовательно, вектор параллелен множеству и, значит, принадлежит .
2)
Рассмотрим произвольный вектор
из множества
![]() .
Отложим его от некоторой точки
.
Отложим его от некоторой точки
![]() :
.
Из леммы о параллельном векторе следует,
что
.
Вектор
:
.
Из леммы о параллельном векторе следует,
что
.
Вектор
![]() также отложим от точки
также отложим от точки
![]() и докажем, что точка
и докажем, что точка
![]() принадлежит множеству
.
Так как
и
принадлежит множеству
.
Так как
и
![]() ,
то имеем
,
то имеем
![]()
![]()
![]() −
=
k
−
=
k![]() −k
=
(1−k)
+
k
.
−k
=
(1−k)
+
k
.
Из
определения аффинного множества
вытекает, что точка
принадлежит
.
Таким образом,
и точки
![]() .
Следовательно, вектор
параллелен множеству
и, значит, принадлежит
.
.
Следовательно, вектор
параллелен множеству
и, значит, принадлежит
.
Из утверждений 1) и 2) следует, что множество − подпространство. ■
Подпространство называется направляющим подпространством аффинного множества .
Вектор
![]() называется перпендикулярным
аффинному
множеству
,
если для каждых двух точек
множества
выполняется условие:
называется перпендикулярным
аффинному
множеству
,
если для каждых двух точек
множества
выполняется условие:
![]() Эту
ситуацию будем обозначать символом
Эту
ситуацию будем обозначать символом
![]() .
Множество всех векторов перпендикулярных
аффинному множеству
обозначим
.
Множество всех векторов перпендикулярных
аффинному множеству
обозначим
![]() .
.
◊ Лемма.
Множество
всех векторов пространства
перпендикулярных аффинному множеству
совпадает с подпространством
![]()
Доказательство вытекает из следующей цепочки равносильных утверждений:
![]()
![]()
![]() .♦
.♦
Подпространство называется нормальным подпространством аффинного множества .
Направляющее подпространство играет значительную роль при изучении аффинных множеств. В нижеследующих теоремах на языке направляющих подпространств решается вопрос о том, когда одно аффинное множество содержится в другом и когда они совпадают.
□Теорема
2.8.
Если точки
![]() принадлежат аффинному множеству
принадлежат аффинному множеству
![]() ,
то аффинная оболочка
,
то аффинная оболочка
![]() содержится во множестве
.
содержится во множестве
.
Доказательство. Используя определение аффинной оболочки, теоремы 2.7, 1.2 и 2-е утверждение леммы о параллельном векторе, имеем следующую цепочку импликаций
![]()
![]()
![]() ■
■
□
Теорема
2.9. Если
аффинные множества
![]() и
и
![]() имеют общую точку
имеют общую точку![]() М
М![]() ,
то справедливы следующие утверждения:
,
то справедливы следующие утверждения:
1)
![]()
![]() ;
;
2)
![]() =
=![]()
![]() .
.
Доказательство.
Необходимость. Если вектор
 ,
то найдутся принадлежащие множеству
такие точки
и
,
что
.
Из условия
следует
,
то найдутся принадлежащие множеству
такие точки
и
,
что
.
Из условия
следует
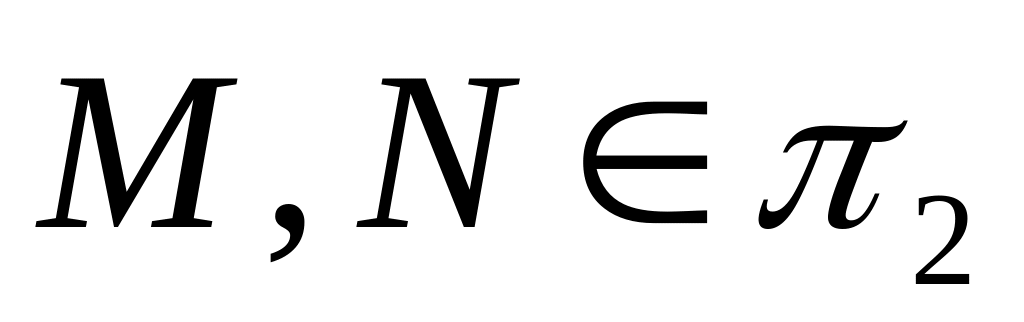 .
Следовательно, вектор
параллелен множеству
и, значит,
.
Следовательно, вектор
параллелен множеству
и, значит,
 .
Этим установлено, что
.
.
Этим установлено, что
.
Достаточность.
Докажем, что![]() .
Пусть точка М
.
Пусть точка М![]() .
По условию точка
.
По условию точка
![]() и, значит, вектор
и, значит, вектор
![]() .
Отсюда и из условия
следует
.
Отсюда и из условия
следует
![]()
![]()
![]() .
Применяя лемму о параллельном векторе,
получаем
.
Применяя лемму о параллельном векторе,
получаем
![]() и,
значит,
и,
значит,![]()
Доказательство этого утверждения использует первое утверждение теоремы 2.5 и вытекает из следующей цепочки импликаций:
=
,
![]() ,
,
![]()
![]() ■
■
○ Примеры
1)
Направляющим подпространством
прямой
в пространстве
или в пространстве
является одномерное векторное
подпространство
![]() ,
где
− ненулевой вектор, параллельный прямой.
,
где
− ненулевой вектор, параллельный прямой.
Решение.
Совпадение подпространств
и
![]() вытекает из следующей цепочки равносильных
утверждений:
вытекает из следующей цепочки равносильных
утверждений:
![]() вектор
вектор![]() параллелен прямой
параллелен прямой
![]() и
и
![]()
коллинеарные
векторы
![]()
2)
Направляющим
подпространством
плоскости
в пространстве
является двумерное подпространство
![]() ,
где
,
где
![]() пара
неколлинеарных векторов, параллельных
плоскости.
пара
неколлинеарных векторов, параллельных
плоскости.
Решение. Рассмотрим следующую цепочку равносильных утверждений:
![]() вектор
вектор
![]() параллелен плоскости
концы векторов
параллелен плоскости
концы векторов
![]() отложенных
от точки плоскости
,
принадлежат
отложенных
от точки плоскости
,
принадлежат
плоскости
![]()
Отсюда
вытекает, что
![]() ●
●
