3. Полупространства в пространствах и
Пусть дана прямая (плоскость) в пространстве (в пространстве ) и – нормальный вектор этой прямой (плоскости). Все точки пространства (пространства ), не принадлежащие прямой (плоскости), разобьем на два множества и . Полупространству принадлежат все точки М пространства (пространства ), для которых векторы и одинаково направлены, где – проекция точки на прямую (плоскость) , т.е.
.
Полупространству принадлежат все точки М пространства (пространства ), для которых векторы и противоположно направлены, где – проекция точки на прямую (плоскость) , т.е.
.
Заметим, каждая точка пространства (пространства ), не принадлежащая , попадает либо во множество , либо во множество . Действительно, если – проекция на прямую (плоскость) , то векторы и коллинеарны. Следовательно, либо , либо .
□ 1. Каждая прямая (плоскость) , заданная уравнением , разбивает пространство (пространство ) на два полупространства и , причем точки полупространства являются решениями неравенства
,
а точки полупространства – решениями неравенства
Доказательство следует из теоремы 2.23.■
□ 2.
Расстояние
от точки
до прямой (плоскости)
,
заданной уравнением
,
находится по формуле:
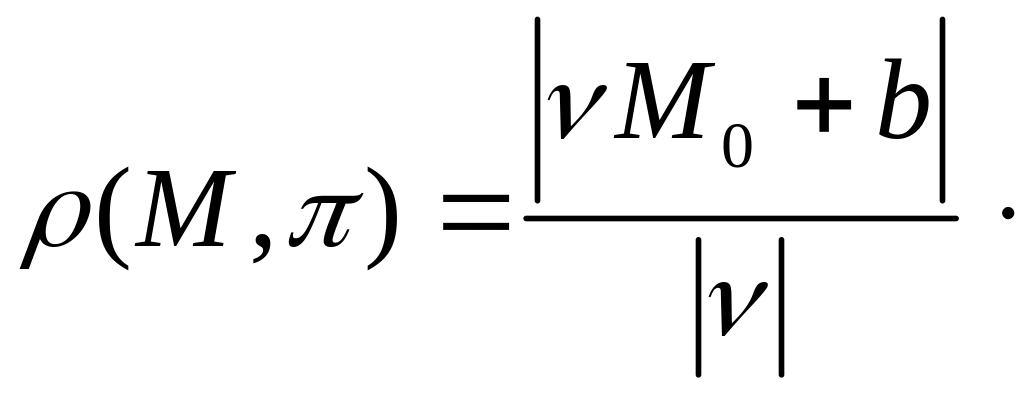
Доказательство вытекает из следствия к теореме 2.23.■
○ Примеры
1.Выяснить,
лежат ли
точки
и
в одном, смежном или в вертикальных
углах, образованных при пересечении
плоскостей
и
,
заданных соответственно уравнениями
,
.
Решение.
Точка
является решением неравенства
,
а точка
решение
неравенства
.
Следовательно, точки
и
лежат в разных полупространствах
относительно плоскости
.
Точки
и
решения неравенства
и, значит, точки
и
находятся в разных полупространствах
относительно плоскости
.
Итак, точки
и
лежат в смежных углах, образованных при
пересечении плоскостей
и
.
2. Написать общее уравнение плоскости , относительно которой точки
находятся в одном полупространстве.
Решение. Векторы
линейно
независимые и образуют базис направляющего
подпространства
.
Нормальный вектор
плоскости
перпендикулярен векторам
и
,
и является решением системы уравнений
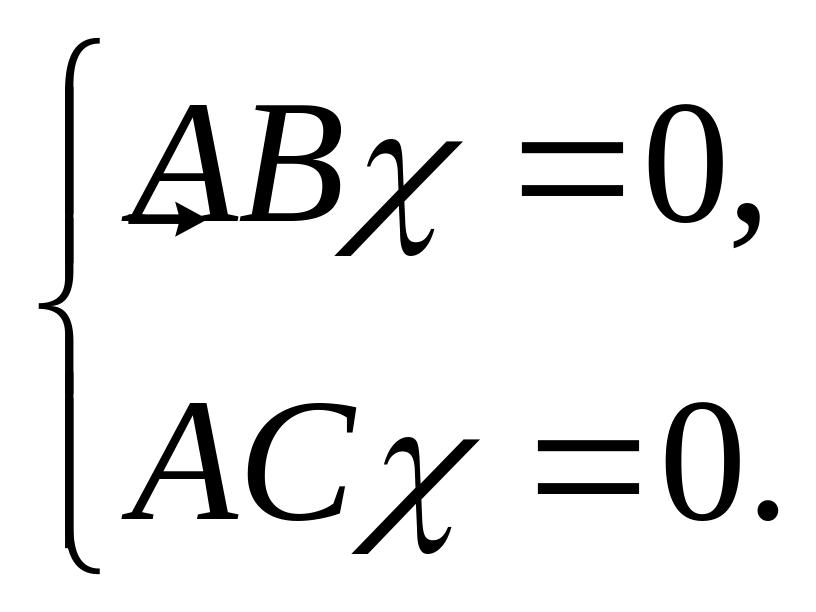
Ее
фундаментальный набор решений содержит
один вектор
.Плоскость
проходит через точку
перпендикулярно вектору
.
Следовательно, общее уравнение этой
плоскости в векторной форме имеет вид
и в координатной форме
.
Координаты
точек
и
являются
решениями этого уравнения. Теперь
уравнение
является
уравнением плоскости, относительно
которой точки
находятся в одном полупространстве,
которое задается неравенством
.
3.
Написать уравнение плоскости
,
находящейся на расстоянии
от плоскости
.
Решение.
Пусть
−
произвольная точка плоскости
.
Тогда, используя следствие к теореме
2.21, будем иметь
Задачи
1.
Дана прямая
.
При каких значениях p
и q
точки
и
:
a) Принадлежат одному полупространству,
b) Находятся в разных полупространствах.
2.Стороны
треугольника заданы уравнениями:
,
,
.
При каких значениях
точка
лежит a)
внутри треугольника, b)
вне треугольника.
3.
Определить, при каких значениях
точки
и
лежат в одном, в смежных или вертикальных
углах, образованных при пересечении
прямых
,
.
4.
Определить, при каких значениях p
точки
и
лежат в одном, в смежных или вертикальных
углах, образованных при пересечении
прямых
,
.
5.
Выяснить, пересекает ли плоскость
отрезок, ограниченный точками
и
.
6. Написать уравнение плоскости, делящей пополам двугранный угол, образованный двумя пересекающимися плоскостями:
а)
,
.
б)
,
.
7.
Написать уравнение плоскости, делящей
пополам тот двугранный угол между двумя
пересекающимися плоскостями
,
,
в котором находится точка
.
8.
Вычислить расстояние между параллельными
плоскостями
,
.
9.Длина
ребра куба равна четырем и
– уравнение одной из его граней. Написать
уравнение параллельной грани куба, если
точка
(3;1;1)
находится внутри куба.
10.
Написать уравнение плоскости, относительно
которой точки
,
,
находятся в одном полупространстве с
точкой
.