2. Определенный интеграл

Пусть дана функция , определённая на [ ], где . Отрезок [ ] точками = разобьём на n элементарных отрезков , , …, , длины которых обозначим через , т. е. , k = 1,2,…,n. В каждом из элементарных отрезков выберем произвольно одну точку , значение функции f( ) умножим на длину отрезка и составим сумму всех таких произведений

S_n = . (2.2)

Сумма (2.2) называется интегральной суммой для функции на [ ].

Обозначим через λ длину наибольшего из элементарных отрезков , т. е. λ = max , k = 1,2,…,n.

Определение 2.1. Определённым интегралом от функции на [ ] называется, конечный предел её интегральной суммы, когда число элементарных отрезков неограниченно возрастает, а длина наибольшего из них стремится к нулю.

Обозначается: , где – называется подинтегральной функцией, – переменной интегрирования, ─ нижним пределом интегрирования, – верхним пределом интегрирования.

Следовательно, по определению

= (2.3)

Из определения следует, что величина определённого интеграла не зависит от обозначения переменной интегрирования, т. е.

= = … = .

Функция, для которой существует предел (2.3), называется интегрируемой на [ ].

Геометрический смысл определённого интеграла состоит в том, что если и f(x) ≥ 0, то определённый интеграл от функции по отрезку [ ] равен площади криволинейной трапеции, ограниченной сверху графиком функции , слева и справа прямыми , снизу  осью .

2. Свойства определенного интеграла

Свойство 2.1. По определению полагаем

= 0.

Свойство 2.2. При перестановке пределов интегрирования определённый интеграл меняет знак на противоположный, т. е.

= − .

Свойство 2.3. Свойство аддитивности.

Если промежуток интегрирования [ ] разбит на конечное число отрезков , , …, , то

= + + … + .

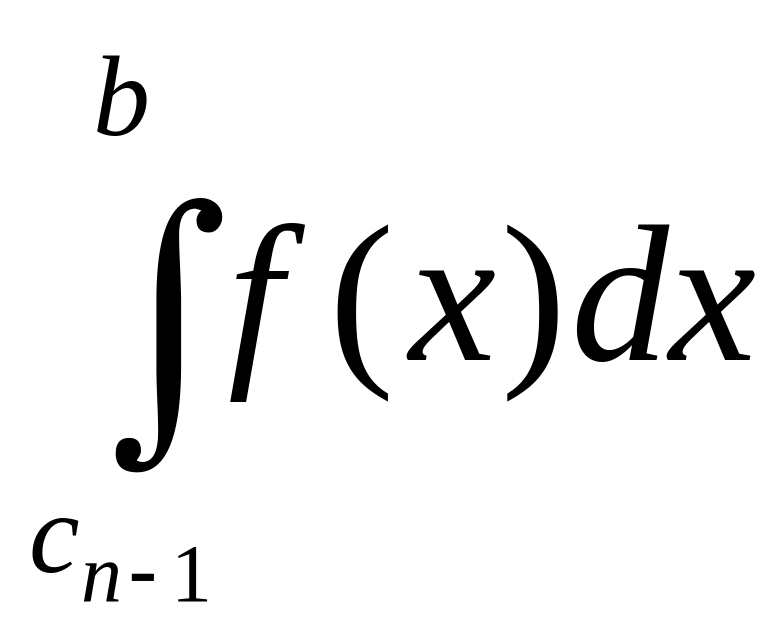Свойство 2.4. Постоянный множитель можно выносить за знак определённого интеграла, т. е. = .

Свойство 2.5. Определённый интеграл от алгебраической суммы конечного числа интегрируемых функций равен алгебраической сумме интегралов от этих функций, = +…+ .

Свойство 2.6. Если функция интегрируема на [ ], где , и ≥ 0 для всех [ ], то ≥ 0.

Свойство 2.7. Если функции , φ(x) интегрируемы на [ ], где , и ≤ φ(x) для всех [ ] , то ≤ .

Свойство 2.8. Если функция интегрируема на [ ], где , то функция │ │ также интегрируема на [ ], причём

.

2.2 Основные теоремы об определенном интеграле

2.2.1 Теорема об оценке определенного интеграла

Теорема 2.1. Если функция интегрируема на отрезке [ ], где , и для всех [ ] выполняется неравенство m ≤ ≤ M, то

m ≤ ≤ M . (2.4)

Неравенство (2.4) позволяет оценить определённый интеграл, т. е. указать границы, между которыми заключено его значение.

Пример 2.1. Оценить определённый интеграл .

В данном случае Так как 3 ≤ 3+ ≤ 4, то

3π ≤ ≤ 4π.