1.4 Основные методы интегрирования

К числу важных методов интегрирования относятся методы: непосредственного интегрирования; замены переменной; интегрирования по частям.

Метод непосредственного интегрирования основан на свойстве 1.4 неопределённого интеграла и использует таблицу основных неопределённых интегралов.

Пример 1.2. ò ( )dx = ò dx + ò dx - ò dx = ℓn + 2 + + C.

Пример 1.3.  dx =  dx =  dx =

=  dx +  dx = tgx – ctgx + C.

Метод замены переменной (или метод подстановки) основан на следующей теореме.

Теорема 1.2. Если F(x) ─ первообразная функции f(x), а х = (t) – дифференцируемая функция f((t))'(t) также имеет первообразную, причём

 f((t))'(t)dt = F((t)) + C.

Доказательство. По правилу дифференцирования сложной функции

(F((t)))' = F'((t))  '(t) = f((t))'(t),

т. е. функция f((t))'(t) имеет в качестве одной из своих первообразных функцию F((t)). Следовательно,

 f((t))'(t)dt = F((t)) + C.

Поскольку

F((t)) + C = F(х) + C =  f(х)dх,

то

 f(х)dх =  f((t))'(t)dt. (1.1)

По формуле (1.1) осуществляется замена переменной в неопределённом интеграле.

Пример 1.4.  sin(2 - 3x)dx = [2 – 3х = t, d(2 – 3x) = dt, -3dx = dt, dx = - dt] = =  sint(- dt) = -  sintdt = cost + C = cos(2 – 3x) + C.

Пример 1.5.  =[ = t - x – подстановка Эйлера, t = x + ,

dt = (1 + )dx, dt = dx, dt = dx, = ] =  =

= ℓnt+ c = ℓnx + + c.

Метод интегрирования по частям основан на следующей формуле

 udv = u  v ─  vdu ,

где u = u(x), v = v(x) ─ некоторые дифференцируемые функции.

Пример 1.6.  хsin2xdx = [u = arctgx, dx = dv, du = (arctgx)'dx, du = dx,

v = x] = xarctgx ─  dx. Вычисляем последний интеграл  dx =

=[t = 1 + x², dt = 2xdx, xdx = dt] =  dt = ℓnt+ C = ℓn1+x²+ C.

Теперь  arctgxdx = x arctgx ─ ℓn1+x²+ C.

Пример 1.7.  e^x cosxdx = [u = e^x, dv = cosxdx, du = e^xdx, v =  cosxdx = sinx] = = e^xsinx ─  e^x sinxdx = [e^x = u, dv = sinxdx, du = e^xdx, v = -cosx] = e^xsinx +

+ e^xcosx -  cosx e^x dx.

Итак,  e^x cosxdx = e^x(sinx + cosx) ─  cosx e^x dx,

2 cosx e^x dx = e^x(sinx + cosx),

 cosx e^x dx = e^x(sinx + cosx) + C.

Вопросы для самоконтроля

1. Какая функция называется первообразной?

2. Что называется неопределенным интегралом oт данной функции?

3. Каковы основные свойства неопределенного интеграла?

4. Назовите основные табличные интегралы.

5. В чем сущность метода непосредственного интегрирования?

6. В чем заключается метод замены переменной (метод подстановки)?

7. В чем заключается метод интегрирования по части?

2 Определённый интеграл и его приложения

2.1 Понятие определенного интеграла

2.1.1 Задачи о площади криволинейной трапеции

Р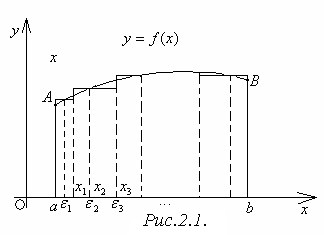 ассмотрим криволинейную трапецию (рисунок 2.1), т. е. плоскую фигуру, ограниченную сверху графиком функции ( ), слева и справа ─ отрезками и прямых , снизу  осью .

Отрезок [ ] точками = разобьём на n элементарных отрезков , , …, , длины которых обозначим через для k = 1,2,…,n. В каждом элементарном отрезке выберем произвольную точку и вычислим в ней значение данной функции f( ). Произведение f( ) выражает площадь прямоугольника с основанием и высотой f( ).

Составим сумму всех таких произведений

S_n = . (2.1)

Эта сумма называется интегральной суммой для функции на [ ] и выражает площадь ступенчатой фигуры, состоящей из прямоугольников и приближённо заменяющей данную трапецию. Очевидно, что сумма S_k зависит от способа разбиения и выбора точек .

Обозначим через λ длину наибольшего из элементарных отрезков , k = 1,2,…,n, т.е. λ = max . Число S, вычисляемое по формуле

S = S_n = ,

называется площадью криволинейной трапеции.