5 Понятие двойного и тройного интегралов

5.1 Двойной интеграл и его свойства

Р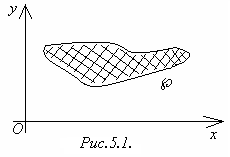 ассмотрим функцию , определённую в области S, которая ограничена замкнутой линией (рисунок 5.1). Область S сетью дуг разобьём на n элементарных областей . Предполагается, что область S и элементарные области имеют площади, которые обозначим теми же символами. В каждой элементарной области произвольно выберем точку М_{k ,} значение функции в этой области умножим на площадь , составим сумму всех таких произведений:

I_n = .

Эта сумма называется интегральной суммой для функции по области S. Обозначим через наибольший из диаметров элементарных областей .

Двойным интегралом от функции по области S называется предел её интегральной суммы при :

= .

Функция называется подинтегральной функцией, а область S – областью интегрирования. Двойной интеграл от функции по области S обозначается также следующим образом:

.

Если предел существует, то функция называется интегрируемой в области S. Отметим, что непрерывные в области S функции всегда интегрируемы.

Геометрический смысл двойного интеграла: двойной интеграл от функции ≥ 0 по области S равен объёму цилиндроида с основанием S, который ограничен сверху поверхностью (рисунок 5.2).

Свойства двойного интеграла.

1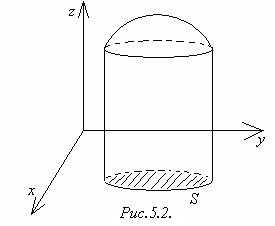 . Если функции и интегрируемы в области S, то интегрируемы в ней их сумма и разность, причём

= ± .

2. Постоянный множитель можно выносить за знак двойного интеграла

= , с = const.

3. Если интегрируема в области S и S разбита на две не пересек-ающиеся области S₁ и S₂, то

= + .

4. Если функции и интегрируемы в области S, в которой ≤ , то ≤ .

5. Если функция интегрируема в области S, то также интегрируема в ней, причём

≤ .

5. Если в области S функция удовлетворяет условиям 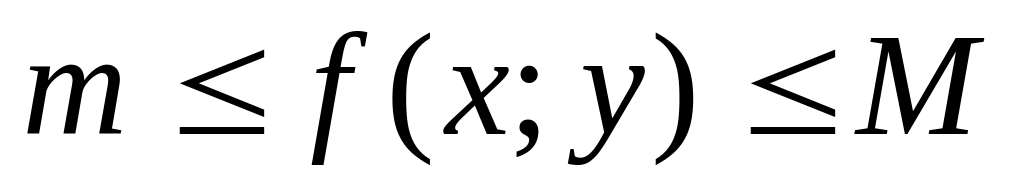, то 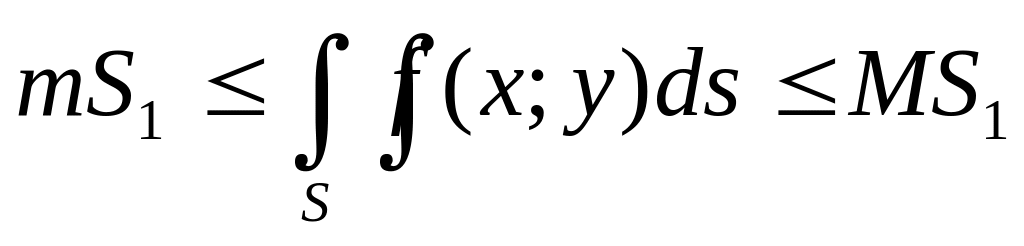, где S₁ ─ площадь области S.

В ычисление двойного интеграла в прямоугольных декартовых координатах.

1. Пусть требуется вычислить двойной интеграл

, (5.1)

где R – прямоугольник, определяемый неравенствами , (рисунок 5.3).

Если функция непрерывна в прямоугольнике R, то (5.1) = .

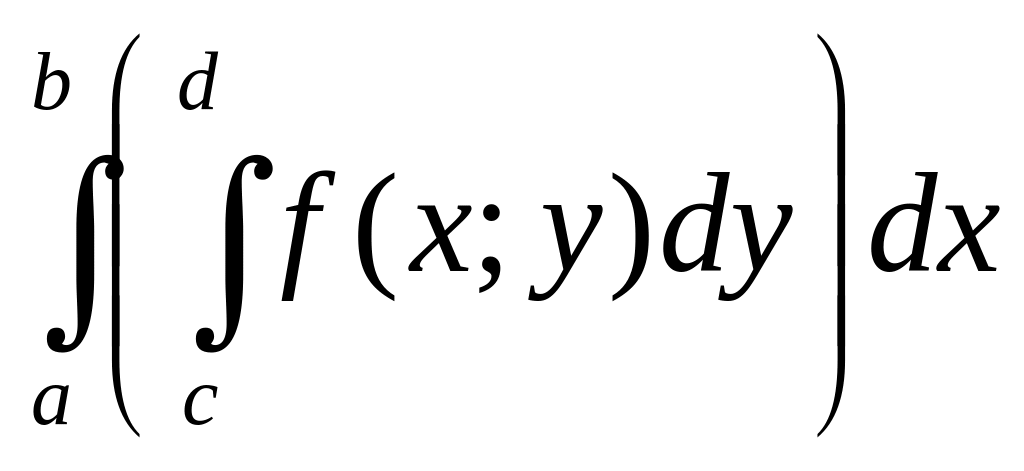Таким образом, вычисление двойного интеграла сводится к вычислению двух определённых интегралов; при вычислении «внутреннего» определённого интеграла считается постоянным. Правая часть формулы (5.1) называется повторным интегралом и обозначается следующим образом: = .

Отметим, что результат интегрирования не зависит от порядка интегрирования, т. е. = .

2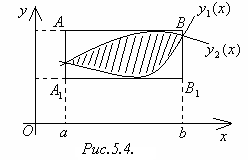 . Чтобы рассмотреть более общий случай, введём понятие стандартной области. Стандартной областью в направлении данной оси называется такая область, для которой любая прямая, параллельная этой оси и имеющая с данной областью общие точки, пересекает границу области только в двух точках, т. е. пересекает саму область и её границу только по одному отрезку прямой.

Предположим, что ограниченная область S является стандартной в направлении оси и ограничена сверху графиком функции , снизу графиком функции (рисунок 5.4).

Пусть АА₁В₁В ─ минимальный прямоугольник, в котором заключена данная область S. Тогда для непрерывной в области S функции

= .

Если же область S является стандартной в направлении оси и определяется неравенствами , , то

= .

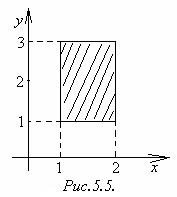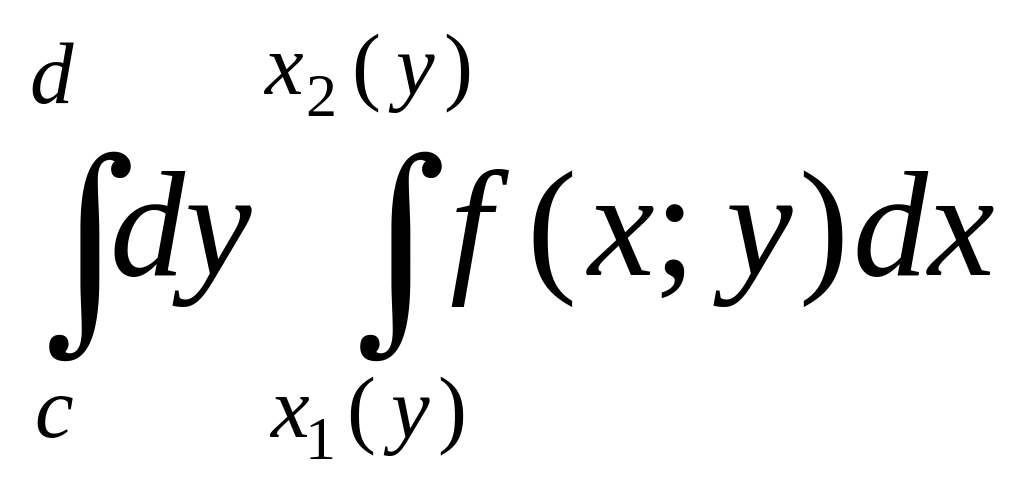Пример 5.1. Вычислить , если

S = (рисунок 5.5).

Решение. Область S является прямоугольником, поэтому = = = = = = = = = 6.

Пример 5.2. Вычислить по области

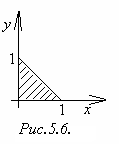S = (рисунок 5.6).

Решение. Область интегрирования изображена на рисунке 5.6. Имеем

= =

= = = = = = = = = .

Замечание 5.1. Если область интегрирования S не удовлетворяет условиям стандартной области, каждая из которых была бы стандартной в направлении одной из осей, и вычислить двойные интегралы по каждой части отдельно.