
Расчет турбины
Поскольку ГТУ
проектируется для привода электрогенератора,
частота вращения ротора установки
принимается равной 50 с
-1. Конечное
давление по параметрам торможения
![]() принимают
равным 105
Па.
принимают
равным 105
Па.
Теплоперепад турбины по параметрам торможения
|
(3.1) |
Значения скоростей во входном и выходном патрубках, перед первой и за последней ступенью, а также КПД входного и выходного патрубка принимают исходя из рекомендуемых значений, приведенных в таблице 3.1.
Давление торможения перед турбиной
|
(3.2) |
Плотность газа перед турбиной по параметрам торможения определяется по следующей формуле:
|
(3.3) |
Таблица 3.1.
Параметры при расчёте турбины
Параметр |
Значение |
Скорость во входном патрубке, ωс |
37 м/с |
Скорость перед первой ступенью, с0 |
80 м/с |
Скорость в выходном патрубке, ωd |
45 м/с |
Скорость за последней ступенью, сz |
115 м/с |
КПД входного патрубка, ηвх |
0,92 |
КПД выходного патрубка, ηвых |
0,55 |
Окружной скорость на диаметре корневых сечений, uк |
189 м/с |
Отношение
скоростей,
|
0,46 |
Угол выхода лопатки в корневом сечении α1к |
15° |
Степень реактивности θк |
0,11 |
Потерz
давления торможения во входном патрубке
вычисляют, приняв
![]()
![]()
![]() :
:
|
(3.4) |
Давление торможения перед первой ступенью
|
(3.5) |
Определяется температура газа за турбиной
|
(3.6) |
|
(3.7) |
Вычисляется температура газов за последней ступенью
|
(3.8) |
Поскольку давление за последней ступенью мало отличается от давления за турбиной, при определении плотности можно принять
|
(3.9) |
Определяется величина потерь полного давления в выходном патрубке:
|
(3.10) |
Давление торможения за последней ступенью турбины
|
(3.11) |
Для определения числа ступеней турбины, вычисляется располагаемый теплоперепад по параметрам перед первой и за последней ступенями:
|
(3.12) |
где
|
(3.13) |
Диаметр корневых сечений dk определяется из условия обеспечения рекомендуемой окружной скорости uк (см. таблицу 3.1)
|
(3.14) |
Рассчитывается располагаемый теплоперепад одной ступени:
|
(3.15) |
- рекомендуемое отношение скоростей (см. таблицу 3.1).
Определяется число ступеней турбины
|
(3.16) |
Вычисляется коэффициент возврата тепла αm
|
(3.17) |
Уточняется теплоперепад одной ступени
|
(3.18) |
Из уравнения неразрывности определяется ориентировочное значение периферийного диаметра первой ступени турбины
|
(3.19) |
(принято cosγ0=0,98).
Высота направляющих лопаток на входе в первую ступень турбины
|
(3.20) |
Для определения
высоты лопаток последней ступени
назначают приемлемое отношение![]() ,
тогда
,
тогда
|
(3.21) |
|
(3.22) |
Находится площадь проходного сечения последней ступени
|
(3.23) |
Меридиональная скорость за последней ступенью сzs определяется из уравнения неразрывности:
|
(3.24) |
Найденное значение сzs вполне приемлемо и может быть принято. Однако в первых ступенях целесообразно принять меньшее значение меридиональной скорости.
Угол выхода лопатки в корневом сечении α1к и степень реактивности θк принимают исходя из рекомендуемых значений (см. табл. 3.1). Коэффициент скорости φ и ζ=1–φ2 =0,05 принимают по опытным данным, представленным в атласах профилей турбин.
Рассчитывается теоретическая скорость за соплами первой ступени, соответствующая изоэнтропийному течению в сопловой решётке
|
(3.25) |
Меридиональная скорость определяется по формуле
|
(3.26) |
Если меридиональная скорость в первой ступени заметно меньше, чем в последней, нецелесообразно выполнять все ступени однотипными. Можно, например, объединить первые несколько ступеней в одну группу, а остальные ступени выполнять индивидуальными.
Существует несколько законов распределения окружных проекций скоростей в ступени турбины. В рамках данного курсового проекта предлагается выполнить расчёт ступени турбины, воспользовавшись законом постоянной меридиональной скорости, описываемый уравнением 3.27. Кроме того, потребуем постоянства работы по высоте лопаток.
|
(3.27) |
Расчет треугольников скоростей производится для трех сечений – корневого, среднего и периферийного.
Определяется средний диаметр в сечении перед соплами
|
(3.28) |
Вычисляется окружная проекция скорости в корневом сечении
|
(3.29) |
После преобразования формулы 3.27, определяется окружная проекцию скорости на среднем диаметре
|
(3.30) |
Меридиональная
проекция относительной скорости
![]() равна меридиональной проекции абсолютной
скорости
равна меридиональной проекции абсолютной
скорости
![]() .
.
Далее вычисляется окружная скорость, проекция относительной скорости на окружное направление и относительная скорость на среднем диаметре
|
(3.31) |
|
(3.32) |
|
(3.33) |
Меридиональная скорость на среднем диаметре с1sc в соответствии с принятым законом распределения скоростей постоянна, т.е. равна с1sк.
Определяется действительное и теоретическое значения абсолютной скорости на среднем диаметре
|
(3.34) |
|
(3.35) |
Располагаемый теплоперепад в рабочей решетке находится по формуле
|
(3.36) |
Вычисляется степень реактивности
|
(3.37) |
Относительная скорость за рабочими лопатками находится по формуле
|
(3.38) |
Средняя меридиональная проекция скорости с2s принимается равной c1s.
Вычисляются
![]()
|
(3.39) |
|
(3.40) |
|
(3.41) |
|
(3.42) |
Желательно,
чтобы значение угла α2
находилось в пределах 70 – 80 °, что может
быть достигнуто, например, путем
небольшого изменения диаметров (т.е.
пара-метра
![]() ).
).
Определяется температура, давление и плотность газа перед рабочими лопатками первой ступени:
|
(3.43) |
|
(3.44) |
|
(3.45) |
|
(3.46) |
Диаметр периферийного сечения находится из уравнения неразрывности
|
(3.47) |
Принято
![]() =
0,98.
=
0,98.
Определяются параметры газа за ступенью
|
(3.48) |
|
(3.49) |
|
(3.50) |
|
(3.51) |
Вычисляется диаметр периферийного сечения на выходе из рабочих лопаток ступени
|
(3.52) |
Принято
![]() =
0,96
=
0,96
Дальнейший расчет газовой турбины предлагается свести в таблицу 3.2.
Таблица 3.2.
Параметры |
Диаметр сечения d, м. |
||
1,2 м |
1,47 м |
1,74 м |
|
Окружная скорость, м/с
|
188,4 |
230,79 |
273,18 |
Окружные проекции скорости, м/с: |
|||
|
371,38 |
306,26 |
260,92 |
|
-35,17 |
-25,62 |
-19,46 |
Меридиональные проекции скорости, м/с: |
|||
с1s (принята постоянной) |
99,5 |
99,5 |
99,5 |
значение
интеграла
|
98,95 |
99,5 |
100,56 |
Угол
|
15º |
18º |
20,9º |
Скорость за направляющими лопатками, м/с:
|
384,44 |
322,99 |
278,92 |
Теоретическая
скорость за направляющими лопатками,
м/с:
|
394,3 |
331,27 |
286,07 |
Располагаемый
теплоперепад направляющих лопаток,
кДж/кг:
|
74,536 |
51,67 |
37,718 |
Окружная проекция относительной скорости, м/с:
|
182,98 |
75,47 |
-12,26 |
Угол
|
28,53º |
52,82º |
97,03º |
Относительная
скорость, м/с:
|
208,32 |
124,88 |
100,25 |
Окружная проекция относительной скорости, м/с:
|
223,57 |
256,41 |
292,64 |
Угол
|
23,87º |
21,2º |
18,96º |
Относительная
скорость, м/с:
|
244,52 |
275,15 |
309,5 |
Теоретическая
относительная скорость, м/с:
|
252,08 |
283,66 |
319,07 |
Располагаемый
теплоперепад на рабочих лопатках,
кДж/кг:
|
10,073 |
32,434 |
45,878 |
Использованный
теплоперепад на рабочих лопатках,
кДж/кг:
|
8,196 |
30,056 |
42,87 |
Общий располагаемый теплоперепад, кДж/кг:
|
84,609 |
84,104 |
83,596 |
Степень
реактивности:
|
0,119 |
0,385 |
0,549 |
Угол
|
70,43º |
75,56º |
79,05º |
Скорость на
выходе из ступени, м/с:
|
105,7 |
102,74 |
102,42 |
Располагаемый
теплоперепад по параметрам торможения,
кДж/кг:
|
82,222 |
82,026 |
81,551 |
Температура газов, К: |
|||
|
1056,07 |
1074,88 |
1086,35 |
|
1052,75 |
1072,53 |
1084,6 |
|
1048,98 |
1048,88 |
1049,26 |
|
1047,36 |
1046,82 |
1046,66 |
Давление, Па·105: |
|||
|
3,65903 |
3,94424 |
4,12629 |
|
3,53886
|
3,54521 |
3,55126 |
Плотность газа, кг/м3: |
|||
|
1,207 |
1,278 |
1,323 |
|
1,175 |
1,178 |
1,179 |
Определяется КПД ступени на расчётных диаметрах:
|
(3.56) |
|
(3.57) |
|
(3.58) |
За КПД ступени допустимо принять среднеарифметическое значение КПД
|
(3.59) |
Определяется величина зазора между корпусом турбины и рабочими лопатками ступени
|
(3.59) |
где
![]() - относительная величина зазора.
- относительная величина зазора.
Влияние утечек оценивают по формуле
|
(3.59) |
где
![]() - опытный коэффициент; l
– длина лопатки
- опытный коэффициент; l
– длина лопатки
Дополнительные потери в ступени возникают также вследствие утечки газа через уплотнения диафрагмы. Их учет может быть произведен после определения размеров диафрагменного уплотнения и расчета утечки через диафрагменное уплотнение.

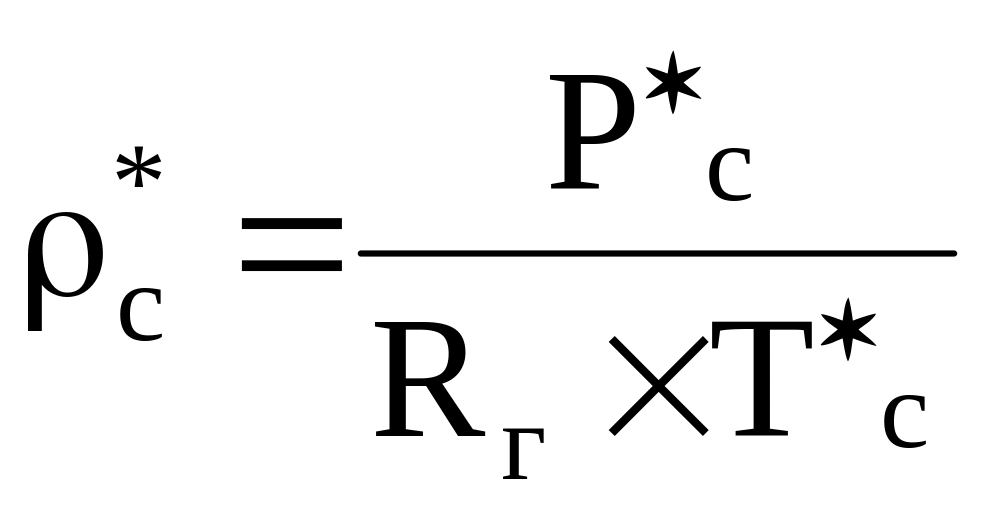 =4,7
10
/(287
1120)=1,46
кг/м
=4,7
10
/(287
1120)=1,46
кг/м
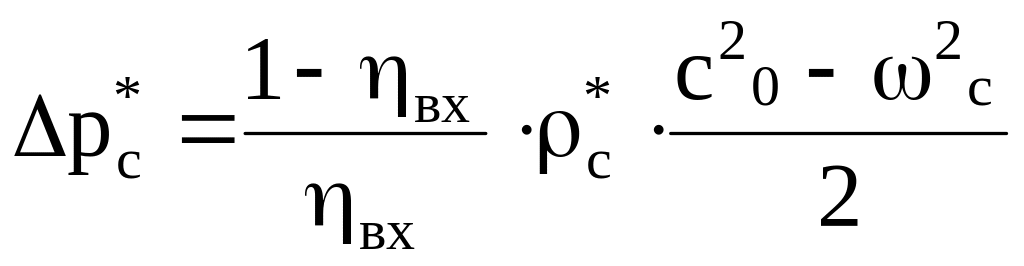 =
=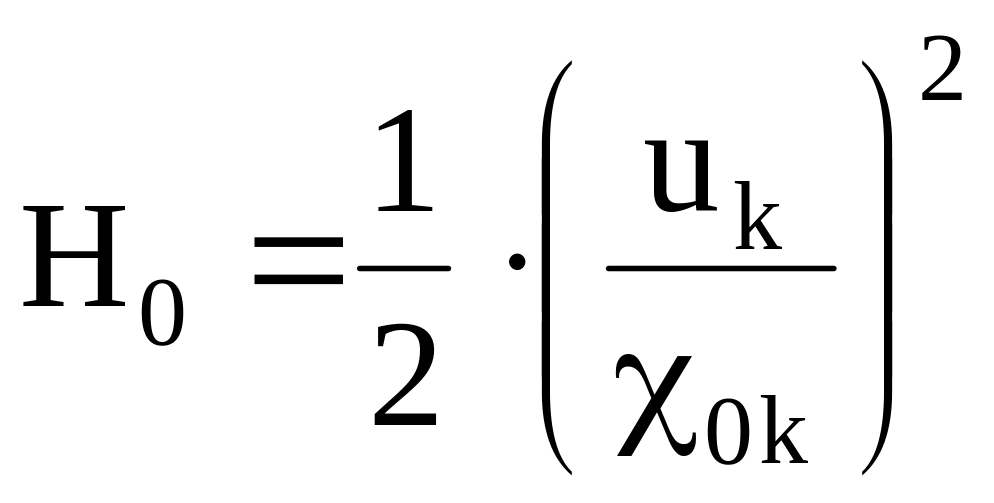 =
=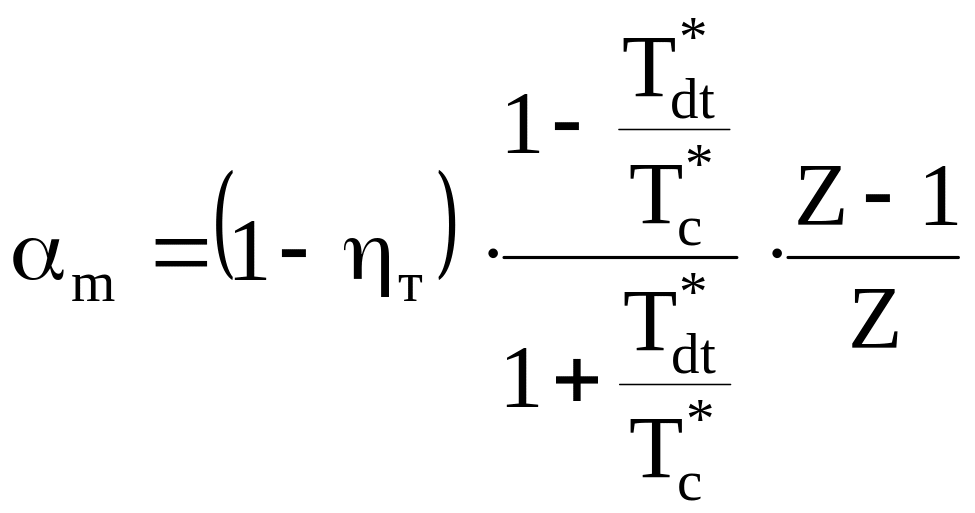 =0,0182
=0,0182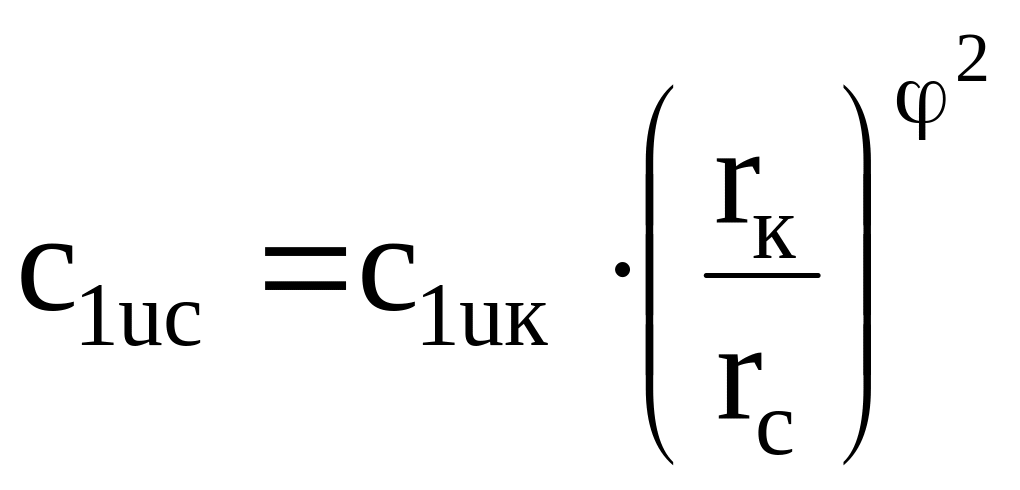 =371,39
=371,39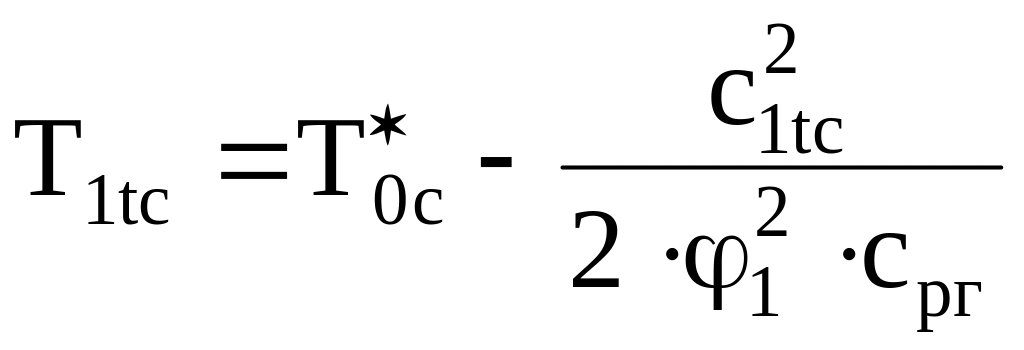 =1120-
=1120-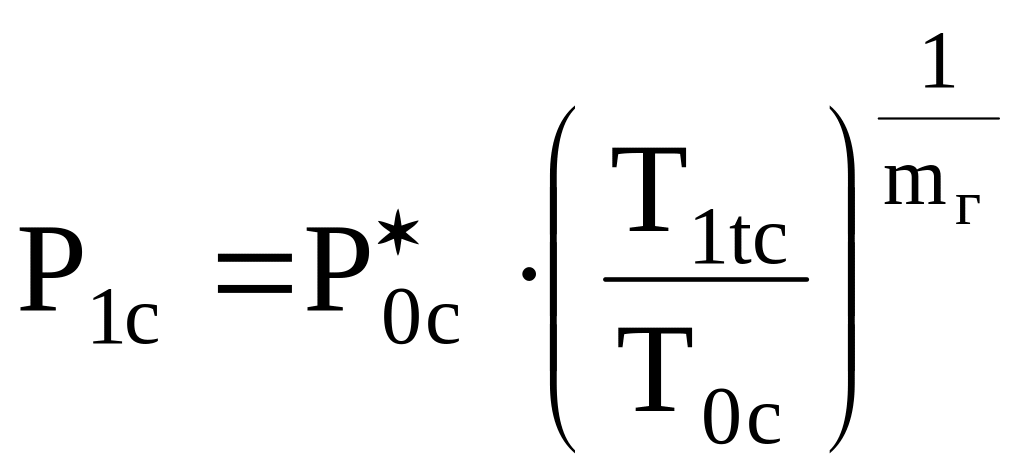 =4,69681
=4,69681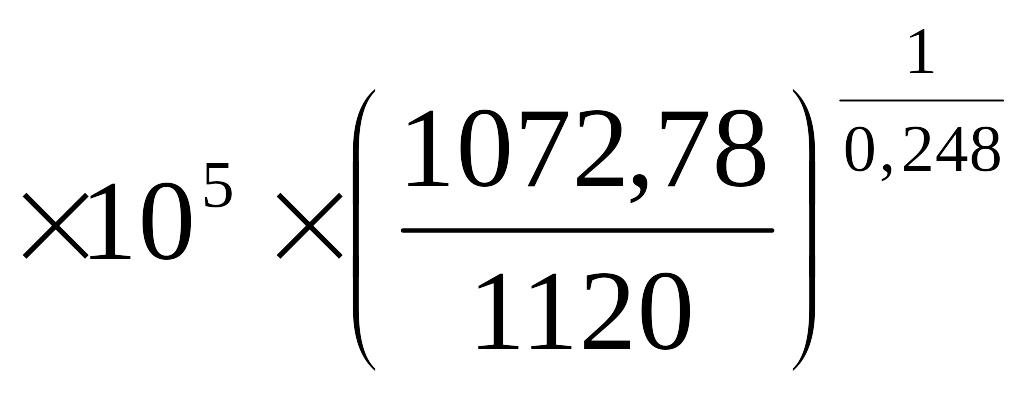 =394795
Па
=394795
Па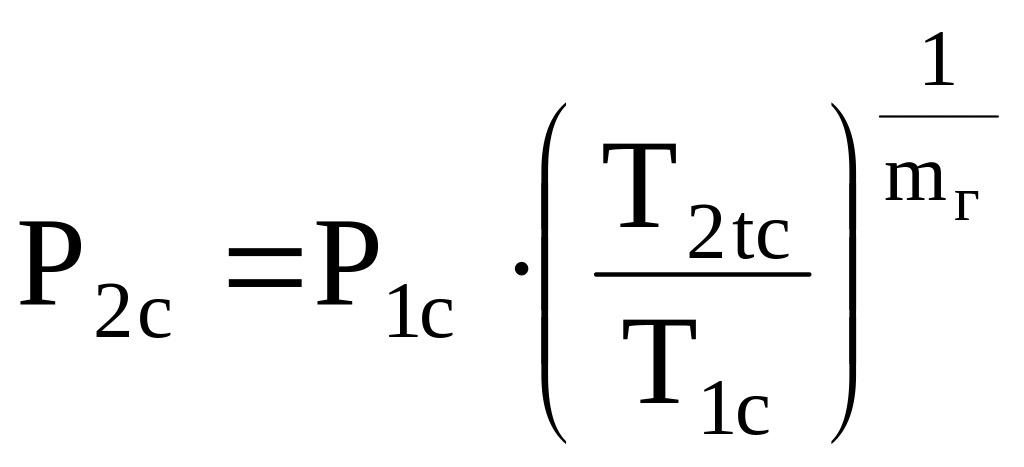 =394795
=394795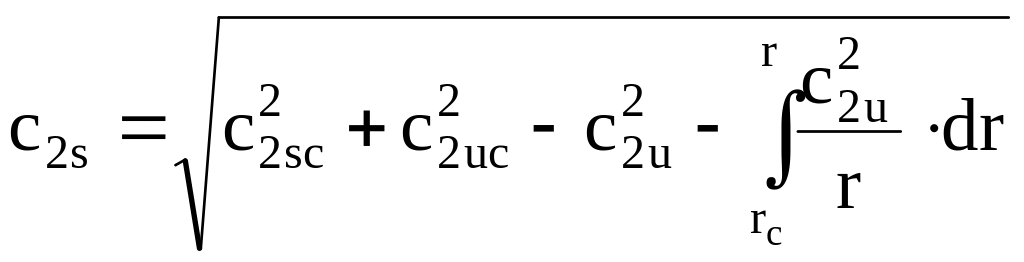 ,
,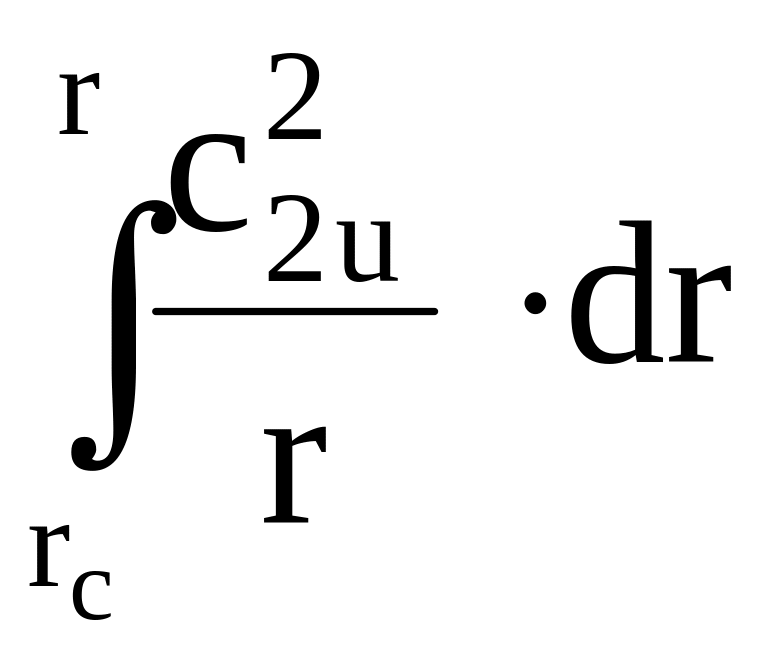 определяется численным интегрированием.
определяется численным интегрированием.
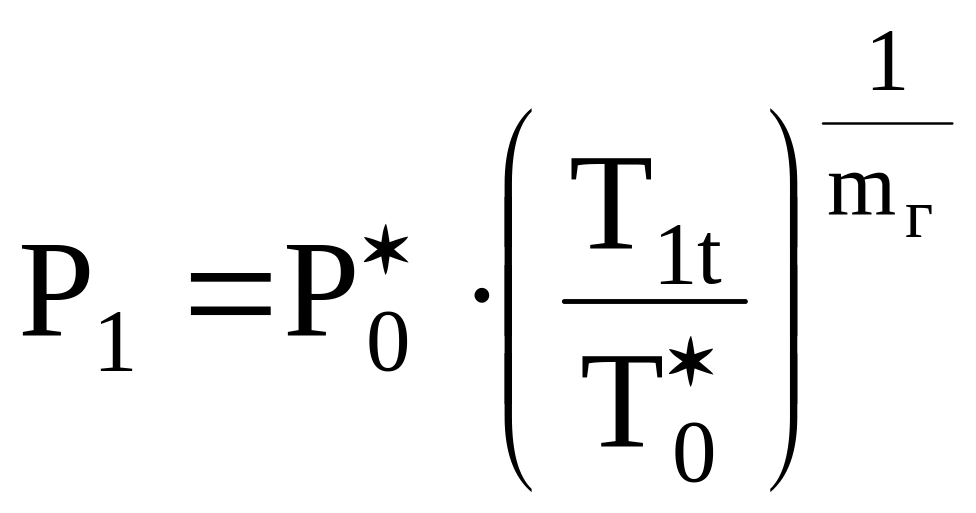
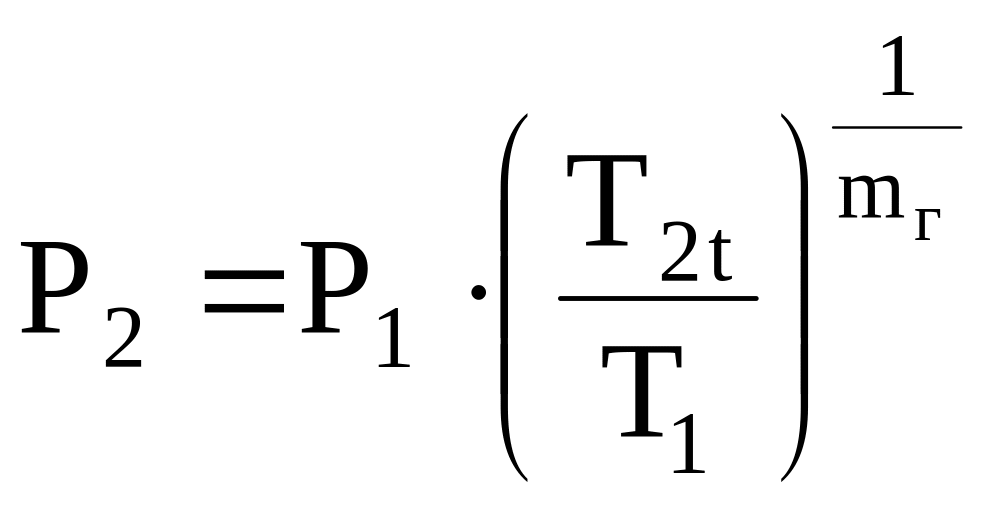
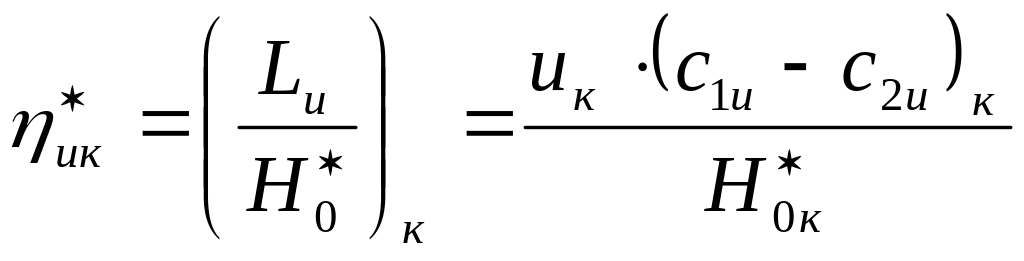 =
=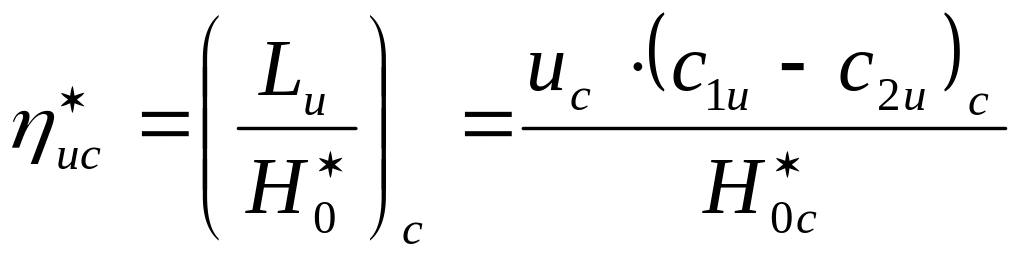 =
=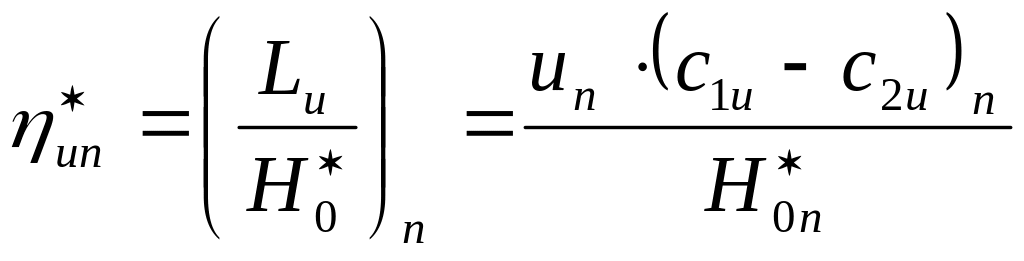 =
=