Частина іі. Кінематика

Кінематика вивчає переміщення тіл в просторі з плином часу без з’ясування причин, які викликають рух. В кінематиці рух тіл вивчається з чисто геометричної точки зору. Якщо в задачі кінематики можна знехтувати розмірами та формою тіла, то тіло замінюють точкою. Траєкторією називається лінія, яку описує точка в процесі руху. До основних кінематичних характеристик відносяться траєкторія, координати (положення), швидкість та прискорення точки і кутова швидкість та кутове прискорення твердого тіла.

Законом руху називається функціональна залежність положення тіла (точки) від часу.

Основні задачі кінематики полягають в тому, щоб:

- знаючи закон руху точки чи тіла відносно обраної системи відліку, встановити основні кінематичні характеристики руху;

- за відомими кінематичними характеристиками встановити закон руху.

§ 1. Способи описання руху точки. Швидкість та прискорення точки

Закон руху точки може бути заданий різними способами:

1 ) натуральний - цим способом зручно користуватись коли відома траєкторія руху точки. Для визначення положення рухомої точки в довільний момент часу потрібно знати (ввести) початок відліку (точку – рис. 1.1) та визначити додатній напрям відліку дугової координати (довжини відрізку траєкторії) і закон руху

, (1.1)

де може приймати як додатне, так і від’ємне значення.

2) векторний - базується на тому, що положення точки в просторі визначається радіус-вектором , проведеним з деякого нерухомого центра до даної точки (рис. 1.2). Під час руху точки її радіус-вектор змінює свій модуль і напрям, тобто є функцією часу

. (1.2)

3) координатний - полягає в тому, що положення точки задається набором координат. При розгляді руху в прямокутній декартовій системі координат вказаний спосіб зводиться до задавання трьох координат , , точки як відомих функцій часу:

, , . (1.3)

Зв’язок векторного метода з координатним наступний

.

В ряді випадків доцільно користуватися координатами циліндричними (рис. 1.3, а):

, , . (1.4)

або сферичними (рис. 1.3, б):

, , . (1.5)

П ерехід від декартової координат до циліндричних, сферичних і навпаки описуються формулами:

а) для циліндричної системи координат:

, , ;

, , .

б) для сферичної системи координат:

, , ;

, , .

В навігації, в основному, користуються циліндричною системою координат на площині (полярною), але дещо зміненою. Замість азимута (рис 1.3, а) використовують курс , який вимірюють від „норду” (напряму на північ) і відлік кута ведуть за напрямом руху стрілки годинника (рис. 1.4). Якщо вісь сумістити з „нордом”, а вісь направити горизонтально, то отримаємо зв’язок між координатами декартової та вказаної систем:

, . (1.6)

Вектор швидкості точки

Нехай в момент часу точка займала положення (рис. 1.5), а в наступн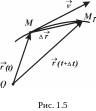 ий момент знаходилась в точці , тоді миттєвою швидкістю точки в момент часу називається величина, яка характеризує зміну вектора з плином часу

. (1.7)

Вектор швидкості точки в даний момент часу дорівнює першій похідній від радіус-вектора за часом і направлений по дотичній до траєкторії у відповідній точці у бік руху (рис. 1.5).

Якщо рівняння руху точки задано в декартових координатах, то

. (1.8)

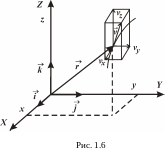
Отже, алгебраїчні проекції вектора швидкості на кожну з осей (рис. 1.6) дорівнюють похідним за часом від відповідної координати точки

, , . (1.9)

Ці алгебраїчні величини однозначно вказують напрям руху точки відносно відповідних осей (вздовж чи проти осі). Модуль вектора швидкості обчислюють за формулою

. (1.10)

Визначимо швидкість руху точки, вважаючи, що рух задано натуральним способом (рис. 1.7). Оскільки дугова координата є функцією часу, то радіус-вектор буде складною функцією часу . Тоді

, (1.11)

д е

= (1.12)

- алгебраїчне значення миттєвої швидкості, а - одиничний вектор (орт), який направлений по дотичній до кривої в сторону зростання дугової координати (рис. 1.7, а, б) і не залежить від напряму руху точки.

Якщо , то точка рухається в напрямі зростання дугової координати і напрям швидкості співпадає з напрямом орта (рис. 1.7, а). При точка рухається в напрямі зменшення дугової координати і вектор швидкості протилежний до напряму орта (рис. 1.7, б). Таким чином, знак алгебраїчного значення швидкості ( = ) однозначно вказує напрям руху точки вздовж траєкторії.

У випадку сталої швидкості (вектор не змінює свій напрям) після інтегрування рівняння (1.7) отримуємо закон руху точки у наступному вигляді

, (1.13)

де – положення точки в момент часу = 0 (початок відліку часу).