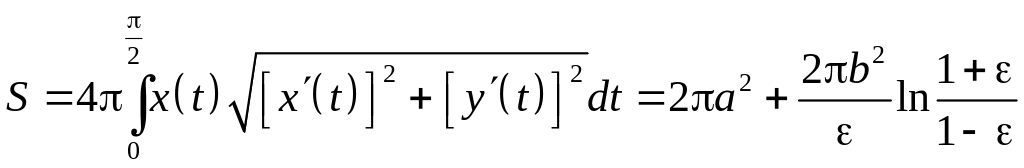6.2. Вычисление объема вращения

Пусть - стандартная относительно оси область. Если ось не пересекает область , то объем тела, образованное вращением области вокруг оси равна

,

если ось не пересекает область , то объем тела, образованное вращением области вокруг оси равна

.

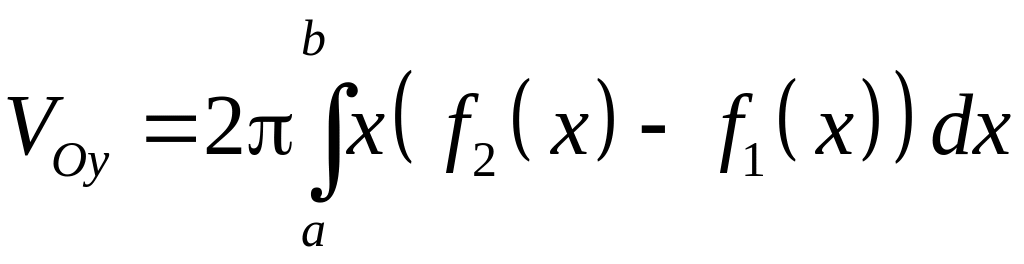Если область ограничена непрерывной замкнутой кривой, заданной параметрически ,

причем при изменении от до кривая проходится так, что область остается слева. Если область не пересекается с соответствующей осью координат и функции и непрерывно дифференцируемы на , то

,

.

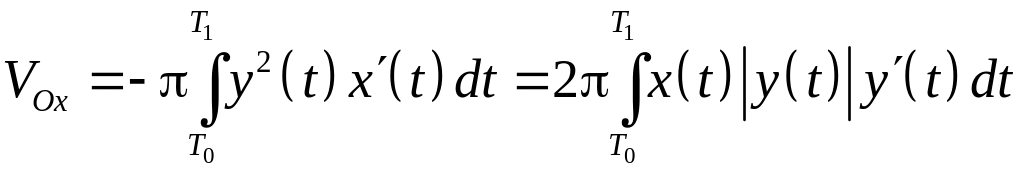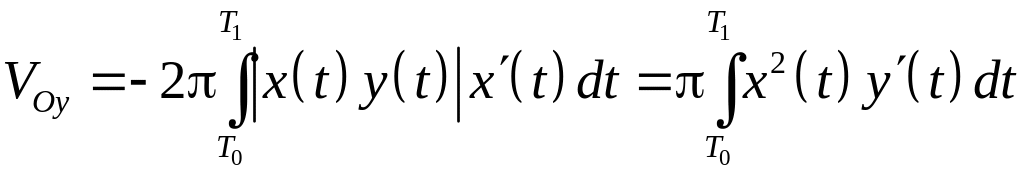Примеры:

6.2.1. Вычислить объём тела, полученного вращением параболы вокруг осей и , ограниченного прямыми и .

n Так как , , , то объем тела, полученного вращением параболы вокруг

,

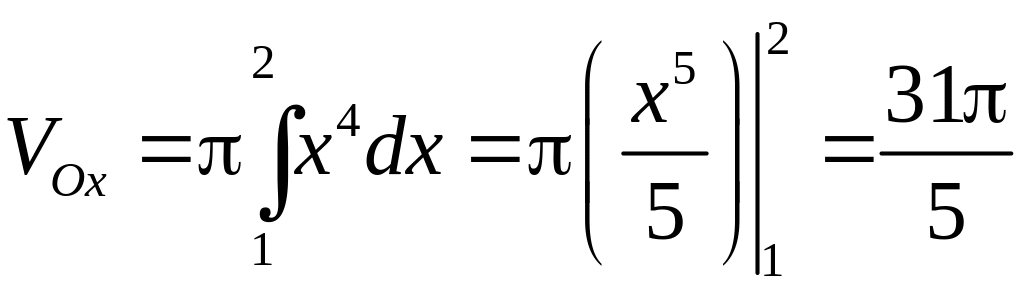вокруг

.ƒ

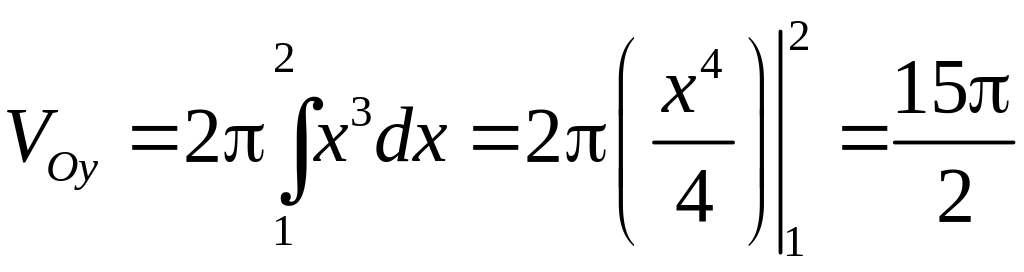6.2.2. Вычислить объем удлиненного и укороченного эллипсоида, образованного вращением эллипса вокруг осей абсцисс (удлиненный эллипсоид) и ординат (укороченный эллипсоид).

n Используем параметрическое параметрическое представление эллипса

, .

Вычисляя производные , . Тогда, при изменении от до , получаем для удлиненного эллипса

,

а для укороченного

.

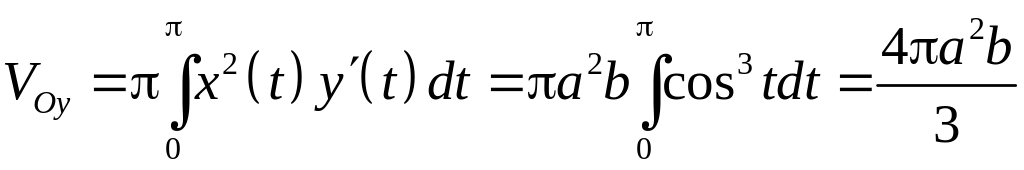Обратим внимание, что в случае шара , его объем равен .ƒ

6.2.3. Вычислить объем тела, образованного вращением астроиды вокруг оси абсцисс.

n Используя параметрическое представление , при изменении параметра в пределах от до , получаем:

, ,

а объем тела равен

.ƒ

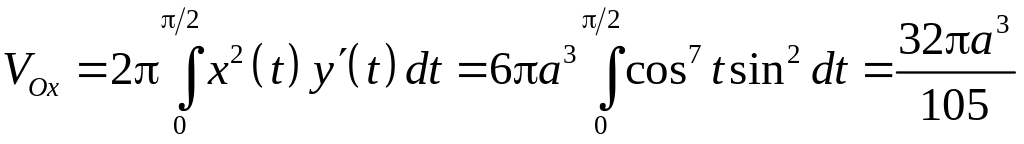6.3. Вычисление длины дуги кривой

Если плоская кривая задана параметрически

, ,

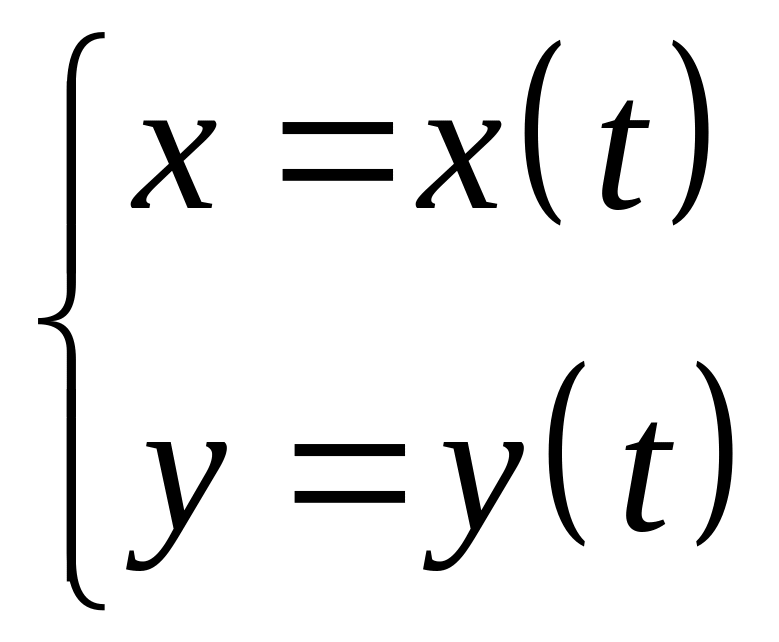причем и - непрерывно дифференцируемые функции, то она имеет длину, вычисляемую по следующей формуле

.

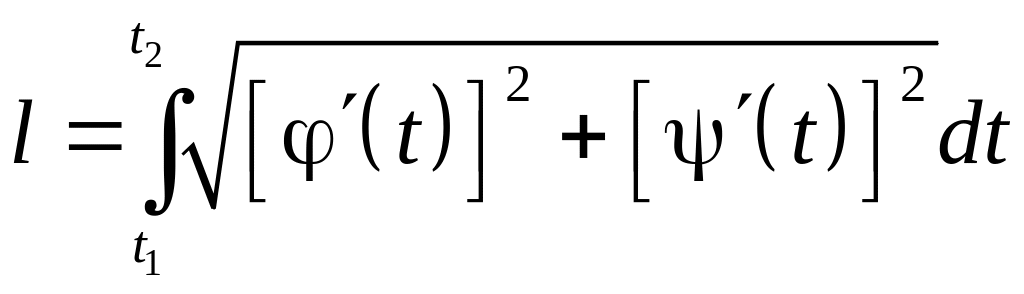Если плоская кривая – график непрерывно дифференцируемой функции и , то длина этой кривой вычисляется по формуле

.

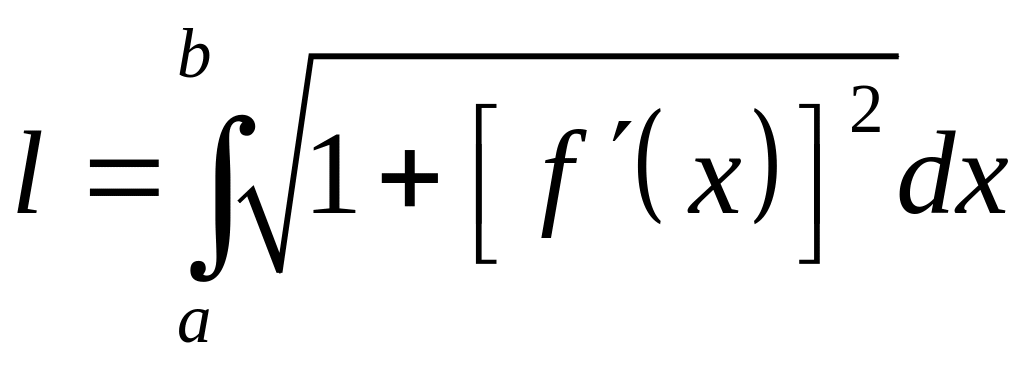В полярных координатах

.

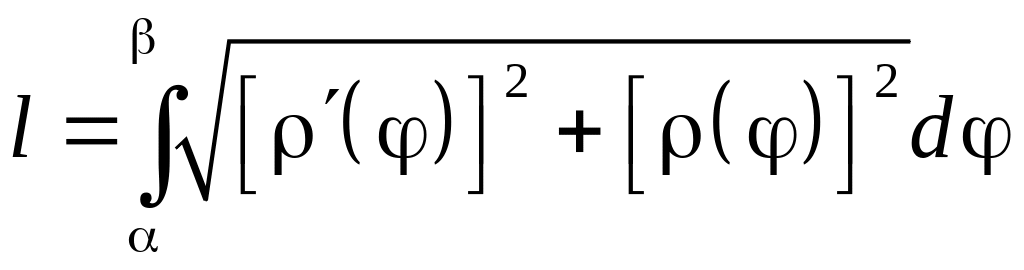Пусть задана дуга кривой и функции непрерывно дифференцируемы на , то дифференциал функции длины дуги называется дифференциалом дуги и вычисляется по одной из формул:

,

,

.

Примеры:

6.3.1. Вычислить длину линии от до .

n Так как , то искомая длина равна

.

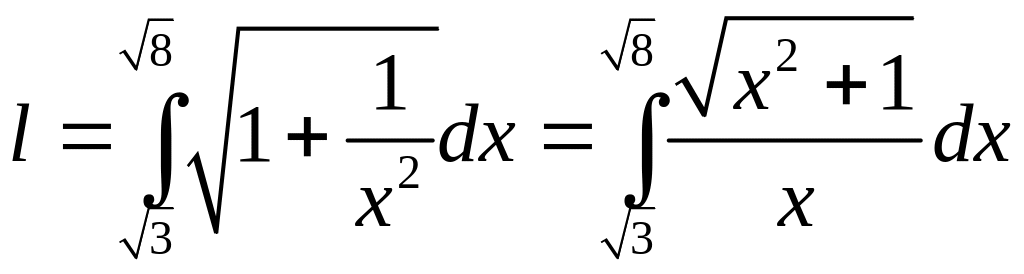Положим , отсюда , 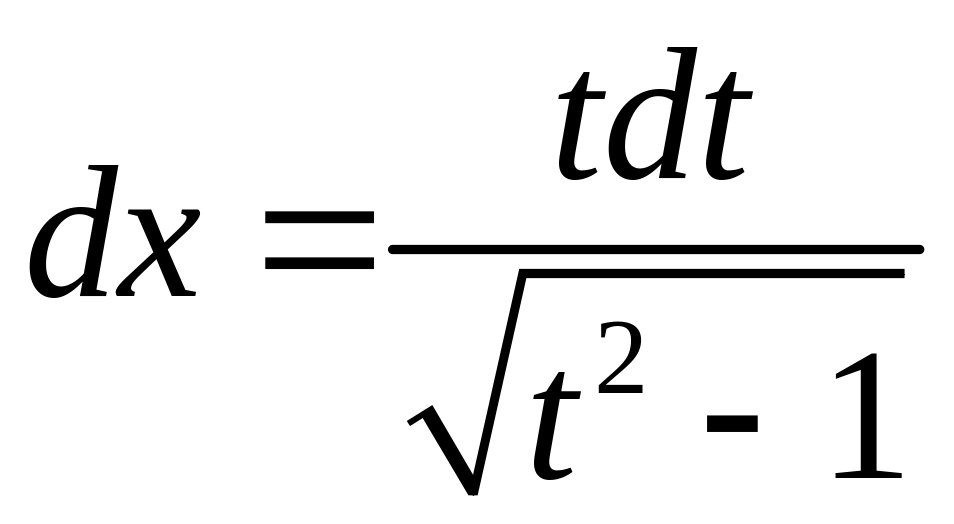. Новые пределы интегрирования: , . Тогда:

ƒ

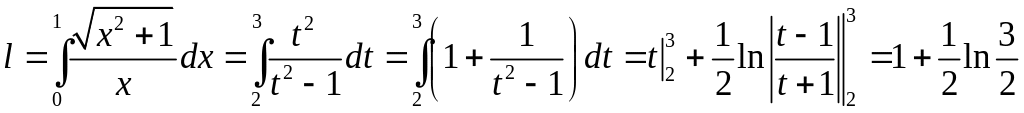
6.3.2. Вычислить длину астроиды, заданной уравнением ( , ).

n Используя параметрическое представление при изменении параметра в пределах от до (первая четверть) и находя производные

и ,

Получаем

.ƒ

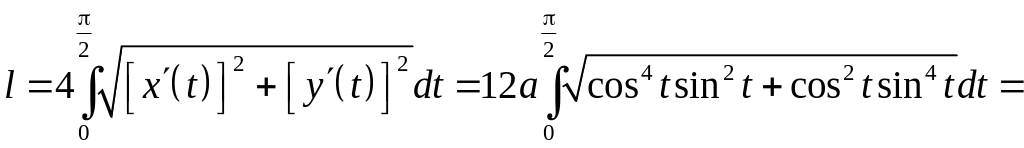
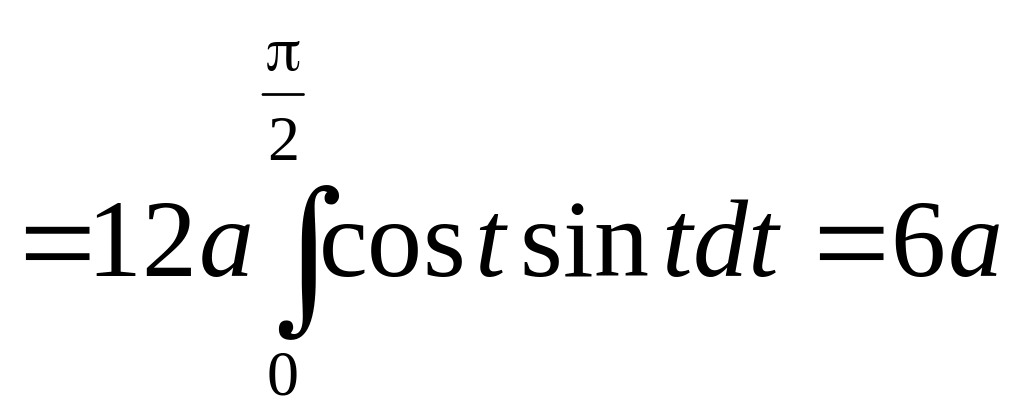6.3.3. Вычислить длину кардиоиды, заданной уравнением .

n Так как , то

.ƒ

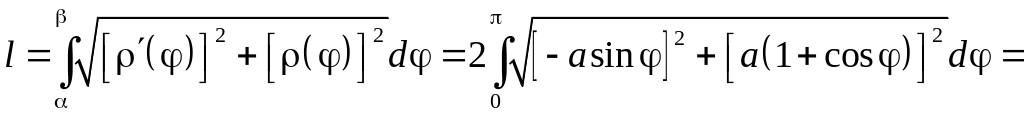
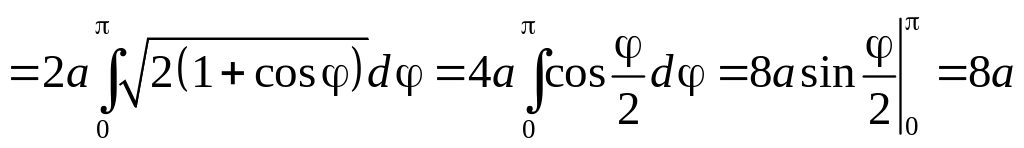6.4. Вычисление площади поверхности вращения

Пусть задана кривая , и прямая , являющаяся осью вращения. Тогда площадь поверхности полученная вращением вокруг оси вычисляется по формуле

,

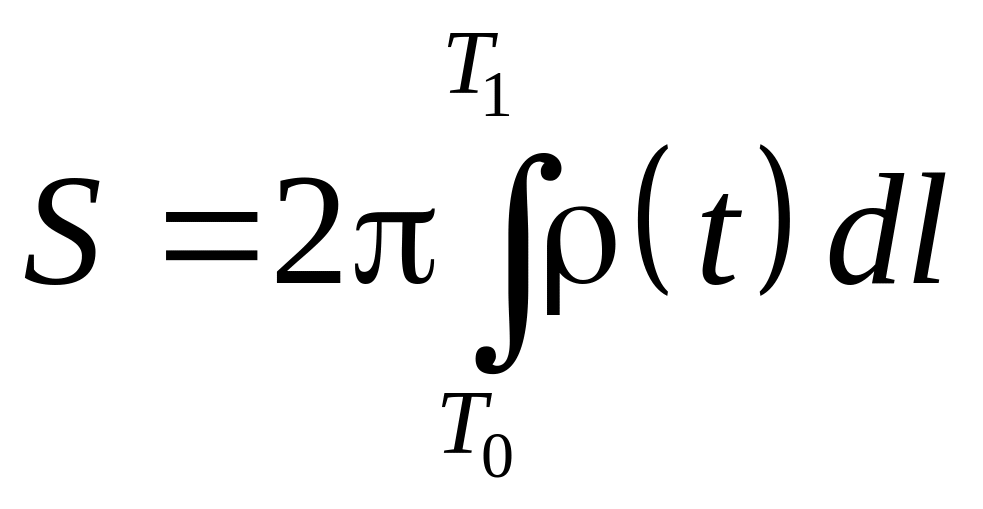где - расстояние от точки , лежащей на кривой , до оси вращения , а - дифференциал дуги .

То есть если поверхность:

а) получается при вращении кривой , вокруг оси , то в качестве параметра вводится переменная , , и искомая площадь равна

.

б) получается при вращении параметрически заданной кривой вокруг оси , то , , а её площадь равна

.

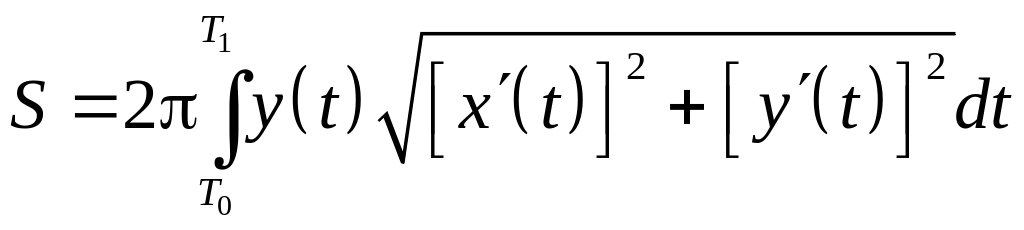в) получается при вращении кривой заданной в полярных координатах вокруг полярной оси, то , , площадь находится по формуле

.

Примеры:

6.4.1. Вычислить площадь поверхности, образованной вращением астроиды, заданной уравнениями , вокруг оси абсцисс.

n Так как

,

,

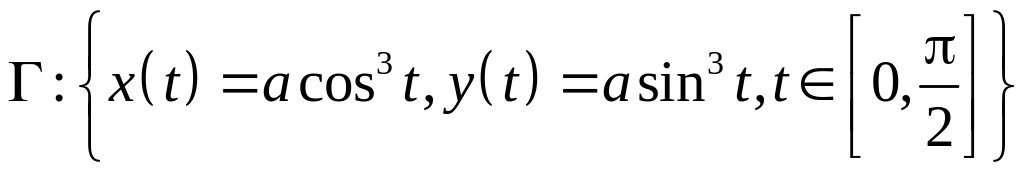то площадь поверхности, получаемой при вращении астроиды равна

ƒ

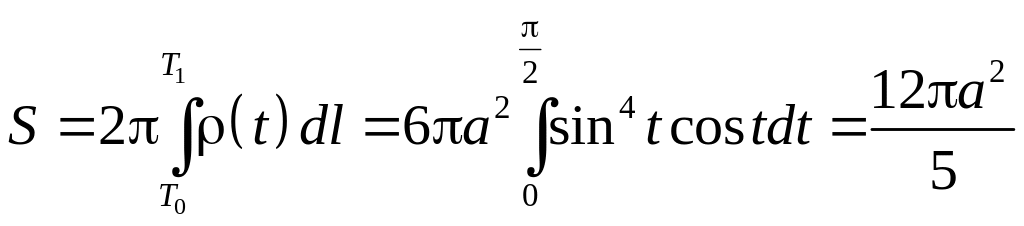
6.4.2. Вычислить площадь поверхности получаемой вращением цепной линии (такая поверхность называется катеноидом) вокруг оси абсцисс и ограниченного двумя плоскостями и , перпендикулярными оси абсцисс.

n Напомним, что

, ,

, .

Тогда площадь поверхности катеноида будет равна

.ƒ

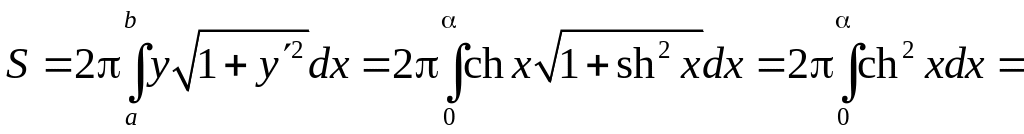
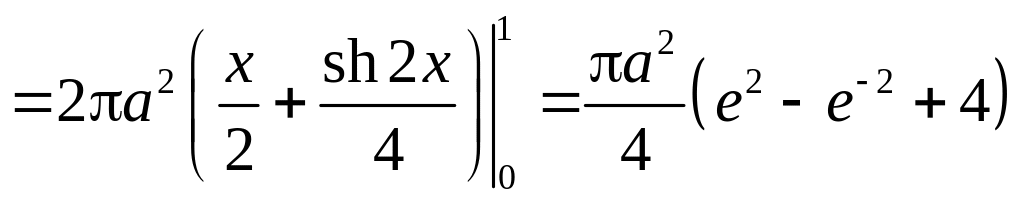6.4.3. Найти площадь поверхности вращения удлиненного и укороченного эллипсоида (см. задачу 6.2.2.).

n Используем параметрическое параметрическое представление эллипса

, .

Вычисляя производные , . Тогда, при изменении от до , получаем для удлиненного эллипсоида

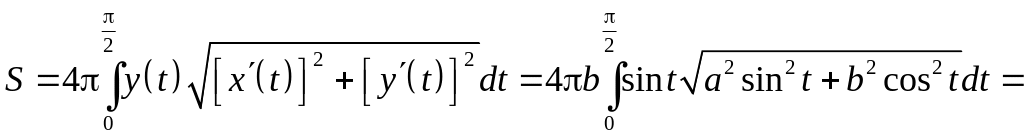
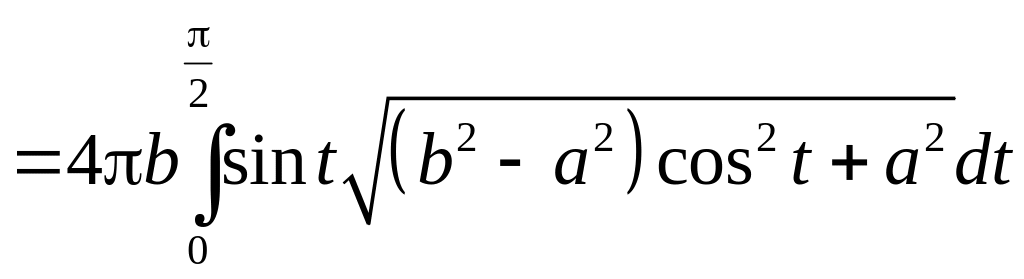
Обозначая - эксцентриситет эллипса, получаем:

.

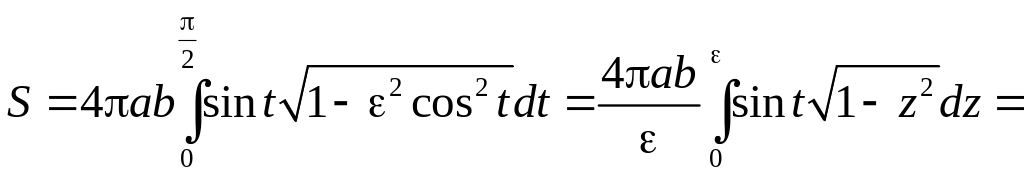
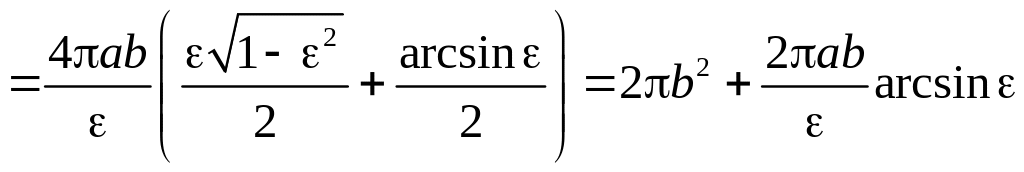Аналогично, для укороченного эллипсоида

ƒ