
- •Часть 2. Определенный интеграл
- •1. Формула Ньютона – Лейбница
- •2. Замена переменных в определенном интеграле
- •3. Формула интегрирования по частям
- •4. Среднее значение функции
- •5. Несобственные интегралы
- •5. 1. Интегралы с бесконечными пределами
- •5.2. Интегралы от функций с бесконечными разрывами
- •6. Геометрические и физические приложения определенного интеграла
- •6.1. Вычисление площади криволинейной трапеции
- •6.2. Вычисление объема вращения
- •6.3. Вычисление длины дуги кривой
- •6.4. Вычисление площади поверхности вращения
- •Задания для самостоятельного решения
- •1. Найти неопредёленный интеграл:
- •5. Найти неопределённый интеграл:
- •6. Найти неопределённый интеграл:
- •7. Найти неопределённый интеграл:
- •8. Найти неопределённый интеграл:
- •9. Найти неопределённый интеграл:
- •10. Найти неопределённый интеграл:
- •Литература
- •Содержание
- •Часть 1. Неопределённый интеграл………………………………………......3
- •Часть 2. Определённый интеграл…………………………….………………49
- •Учебное издание Александр Борисович Дюбуа Светлана Николаевна Машнина
4. Среднее значение функции
Пусть
интегрируема и ограничена на
и
![]() ,
,
![]() — соответственно, верхняя и нижняя
грани
на отрезке
.
Тогда, существует такое число
— соответственно, верхняя и нижняя
грани
на отрезке
.
Тогда, существует такое число
![]() ,
что:
,
что:
![]() и
и
 .
.
Число
 называется средним значением функции
называется средним значением функции
![]() на отрезке
.
на отрезке
.
Примеры:
4.1. Вычислить
среднее значение функции
![]() на отрезке
на отрезке
![]() .
.
По формуле среднего значения функции на интервале, получаем
 .◄
.◄
4.2. Вычислить
среднее значение функции
![]() на отрезке
на отрезке
![]() .
.
По формуле среднего значения функции на интервале, получаем
 .◄
.◄
4.3. Вычислить
среднее значение функции
![]() на отрезке
на отрезке
![]() .
.
По формуле среднего значения функции на интервале, получаем
 .◄
.◄
5. Несобственные интегралы
5. 1. Интегралы с бесконечными пределами
Если
непрерывна на интервале
![]() ,
то интеграл
,
то интеграл

называется
несобственным интегралом от
.
Если предел существует и конечен,
интеграл называется сходящимся, если
нет, то расходящимся. Если
![]() при
при
![]() ,
то при
,
то при
![]() интеграл сходится, при
интеграл сходится, при
![]() интеграл расходится.
интеграл расходится.
Отметим важные примеры несобственных интегралов:
 - интеграл Пуассона,
- интеграл Пуассона,
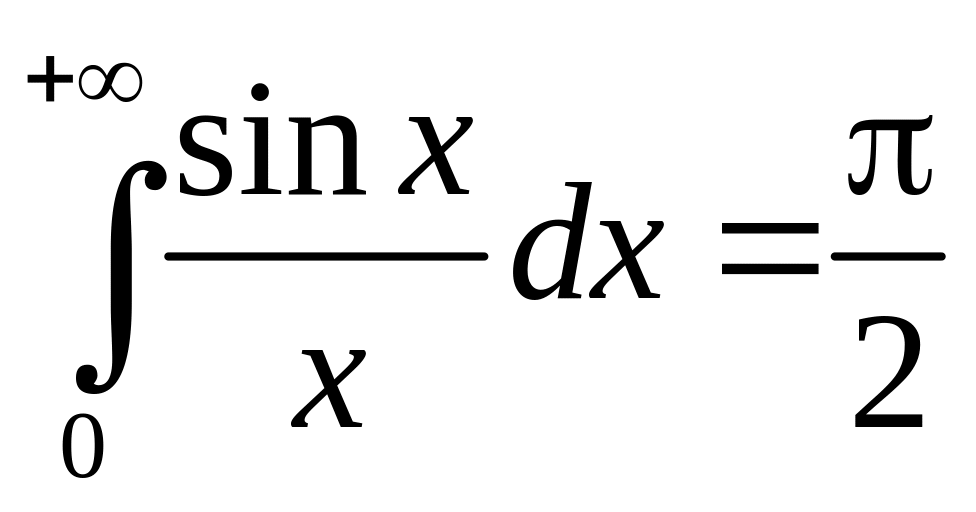 - интеграл Дирихле,
- интеграл Дирихле,
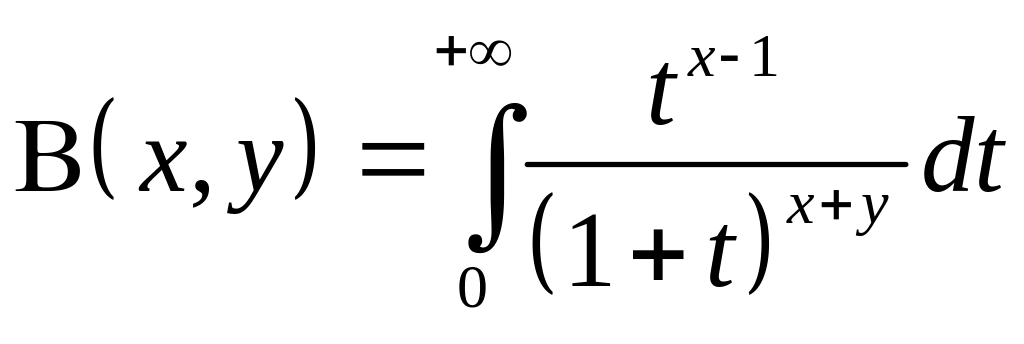 - Бета-функция
(эйлеров интеграл 1 рода),
- Бета-функция
(эйлеров интеграл 1 рода),
 - Гамма-функция
(эйлеров интеграл 2 рода).
- Гамма-функция
(эйлеров интеграл 2 рода).
Примеры:
5.1.1. Вычислить
интеграл
![]()
Найдём
 .
.
Предел существует и конечен. Значит, интеграл сходится. ◄
5.1.2. Вычислить
интеграл

Найдём
 .
.
Предел не существует. Несобственный интеграл расходится. ◄
5.1.3. Вычислить
интеграл .
.
Подынтегральная функция чётная, поэтому
 .
.
Вычислим интеграл:
 .
.
Получили
 .
Интеграл сходится. ◄
.
Интеграл сходится. ◄
5.1.4. Доказать
расходимость интеграла .
.
Так как при
![]() ,
,
 ,
то вычисляя
интеграл
,
то вычисляя
интеграл
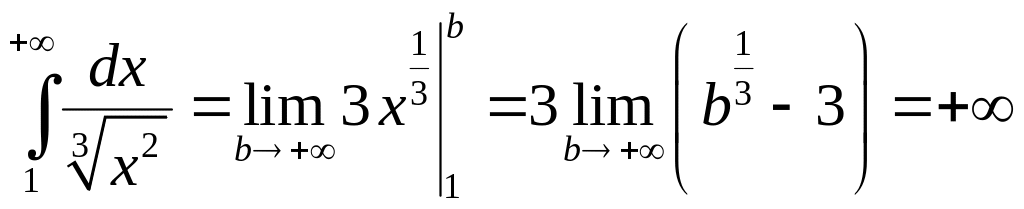 .
.
Этот интеграл расходится. Следовательно, по признаку сравнения исходный интеграл тоже расходится.
5.2. Интегралы от функций с бесконечными разрывами
Если
непрерывна на
![]() и неограниченна в любой окрестности
точки
и неограниченна в любой окрестности
точки
![]() ,
то интеграл
,
то интеграл

называется
несобственным интегралом от
.
Если предел существует и конечен,
интеграл называется сходящимся, если
нет, то расходящимся. Если
![]()
![]() при
при
![]() ,
то при
,
то при
![]() интеграл сходится, при
интеграл сходится, при
![]() интеграл расходится.
интеграл расходится.
Примеры:
5.2.1. Исследовать
на сходимость интеграл .
.
Так как
подынтегральная функция
![]() терпит
разрыв в точке
терпит
разрыв в точке
![]() ,
то получим:
,
то получим:
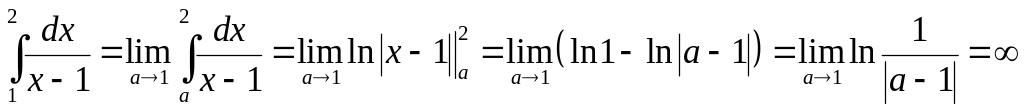
Конечного предела не существует, значит, интеграл расходится. ◄
5.2.2.
Исследовать на сходимость интеграл
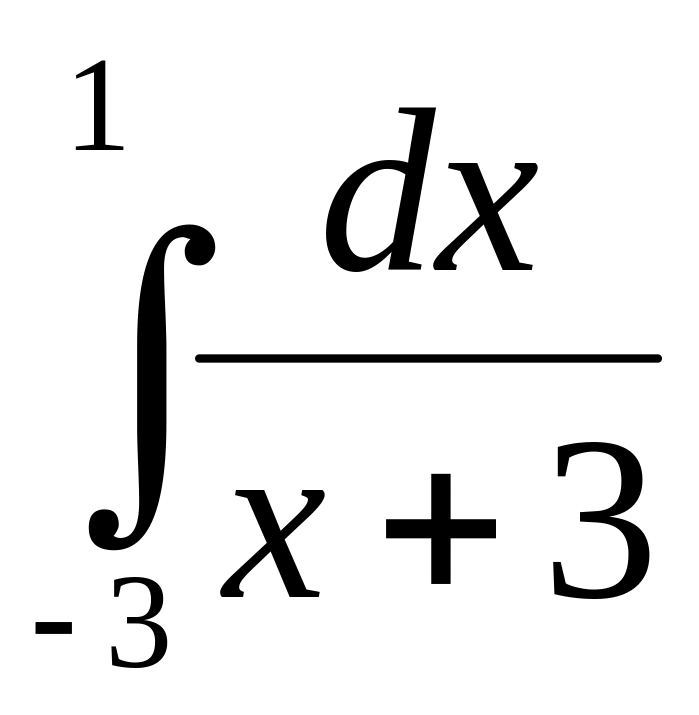
Так как
подынтегральная функция
![]() терпит
разрыв в точке
терпит
разрыв в точке
![]() ,
то получим:
,
то получим:
 .
.
Конечный предел равен бесконечности. Значит, интеграл расходится. ◄
5.2.3. Исследовать
на сходимость интеграл

Так как
подынтегральная функция
![]() терпит
разрыв в точке
терпит
разрыв в точке![]() ,
получим:
,
получим:
 .
.
Применим
интегрирование по частям. Пусть
![]() Тогда
Тогда
![]() .
.
И первоначальный интеграл примет вид:
 .
.
Предел конечен. Поэтому интеграл сходится. ◄
5.2.4. Исследовать на сходимость интеграл
Имеем
 .
.
Предел бесконечен. Следовательно, интеграл расходится. ◄
6. Геометрические и физические приложения определенного интеграла
6.1. Вычисление площади криволинейной трапеции
Площадь плоской
области
![]() стандартной относительно оси
стандартной относительно оси
![]() ,
ограниченной прямыми
,
ограниченной прямыми
![]() и
и
![]() и кривыми
и кривыми
![]() ,
,
![]() такими, что для любых
такими, что для любых
![]() выполнено
выполнено
![]()
(т.е.![]() )
вычисляется
)
вычисляется
 .
.
Аналогично площадь
плоской области стандартной относительно
оси
![]() ,
ограниченной прямыми
,
ограниченной прямыми
![]() и
и
![]() и кривыми
и кривыми
![]() ,
,
![]() такими, что для любых
такими, что для любых
![]() выполнено
выполнено
![]() (т.е.
(т.е.![]() )
вычисляется
)
вычисляется
 .
.
Если область ограничена непрерывной замкнутой кривой, заданной параметрически
![]() ,
,
то её площадь можно вычислить по одной из трёх формул
 ,
,
 ,
,
 .
.
Какую из них удобнее
применять, зависит от конкретного вида
функций
![]() и
и
![]() .
.
Площадь области
:
![]() ,
,
называемой
криволинейным сектором, ограниченной
графиком
![]() и двумя лучами, составляющими с полярной
осью углы
и двумя лучами, составляющими с полярной
осью углы
![]() и
и
![]() имеет площадь
имеет площадь
 .
.
Примеры:
6.1.1.
Вычислить площадь области, ограниченной
линиями:
![]() и
и
![]() .
.
Изобразим фигуру в декартовой системе координат:
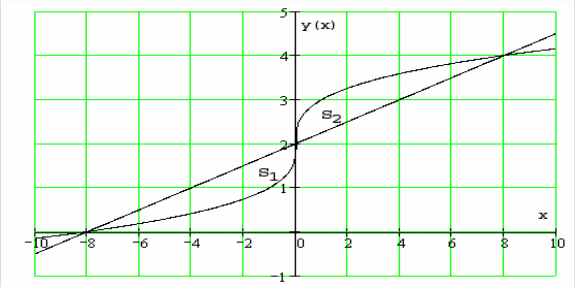
Из условия симметрии
фигуры относительно точки с координатами
![]() ,
площади
,
площади
![]() и
и
![]() равны. Так как данная область является
стандартной как относительно оси
так и относительно оси
,
то ее площадь можно вычислить одним из
двух способов.
равны. Так как данная область является
стандартной как относительно оси
так и относительно оси
,
то ее площадь можно вычислить одним из
двух способов.
1) Выразим зависимости в явном виде:
![]() и
и ![]() ,
,
а стандартная относительно оси область
 .
.
Тогда получаем
 .
.
2) Заметим, что для вычисления площади можно было воспользоваться исходным видом зависимостей:
![]()
 .
.
6.1.2.
Вычислить площадь области, ограниченной
параболами
![]() и
и
![]() .
.
Изобразим фигуру в декартовой системе координат

Очевидно, область симметрична относительно оси , кроме того, она не является стандартной относительно оси и стандартной относительно оси , а ее площадь можно вычислить одним из двух способов.
Данная область не является стандартной относительно оси . Её можно разбить на две стандартные относительно оси области:
![]() ,
,
![]() .
.
Из симметрии
областей
![]() и
и
![]() относительно оси
следует, что
относительно оси
следует, что

 .
.
Относительно оси данная область является стандартной:
 .
.
Снова, используя симметрию области, получаем
 .
.
6.1.3.
Вычислить площадь эллипса, заданного
уравнением
![]() (
(![]() ,
,
![]() ).
).
Искомую площадь можно вычислить, используя как явное представление линии, так и параметрическое.
Выразив уравнение в явном виде
![]() ,
,
получим,
применив подстановку
,
![]() ,
приходим к
,
приходим к
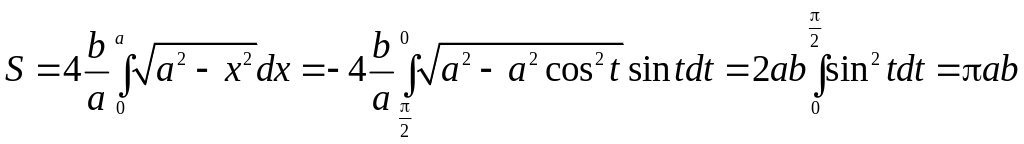 .
.
2) С другой стороны,
используя параметрическое представление
,
при изменении параметра
![]() в пределах от
в пределах от
![]() до
до
![]() ,
получаем:
,
получаем:
 .
.
6.1.4.
Вычислить площадь астроиды, заданной
уравнением
![]() (
(![]() ,
,![]() )
)
Изобразим кривую в декартовых координатах:

Используя параметрическое представление , при изменении параметра в пределах от до , получаем:

 .
.
6.1.5.
Найти площадь фигуры, ограниченной
кардиоидой
![]() ,
,
![]() .
.
Изобразим кривую в декартовых координатах:
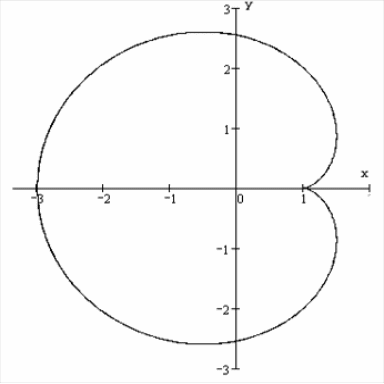
Так как кардиоида
симметрична относительно оси
,
то, используя параметрическое
представление, будем менять параметр
в пределах от
до
![]() .
Так как
.
Так как
![]() и
и ![]() ,
,
получаем по любой из трех формул



 ,
,


 ,
,

 .
.
Отметим, что площадь
кардиоиды задаваемой уравнением в
полярных координатах
![]() равна
равна
 .
.
6.1.6.
Найти площадь области, ограниченной
кривой
![]() .
.
Кривая образует три симметричные петли, каждая из которых ограничивает криволинейный сектор. Изобразим ее в полярных координатах.

Рассмотрим сектор, лежащий в первой четверти:
![]() .
.
Площадь его, очевидно, равна 1/3 площади всей области, ограниченной данной кривой. Следовательно,
 .
.
