Часть 2. Определенный интеграл
1. Формула Ньютона – Лейбница
Для вычисления
определенного интеграла основной
является теорема Ньютона – Лейбница:
если
непрерывна на
и
первообразная для
на
,
то
.
Примеры:
1.1.
Вычислить определенный интеграл
.
Вычислить определенный интеграл
Применим табличный интеграл:
.
1.3. Вычислить определенный интеграл
.
Вычислить определенный интеграл
Применяя соотношения между тригонометрическими функциями, получаем
2. Замена переменных в определенном интеграле
Формула
справедлива при следующих условиях:
Функция непрерывна на отрезке ;
Отрезок является множеством значений функции
,
определенной на отрезке
;
;
.
Примеры:
2.1. Вычислить определенный интеграл
Применим метод
интегрирования замены переменной. Пусть
,
тогда
.
Найдём новые пределы интегрирования.
Если
,
то
;
если
,
то
.
С учётом замены, получаем:
.◄
2.2. Вычислить
определенный интеграл
.
Применим метод
интегрирования замены переменной. Пусть
.
Тогда
,
,
.
Найдём новые пределы интегрирования.
Если
,
то
;
если
,
то
.
Тогда интеграл примет вид:
.◄
2.3. Вычислить
определенный интеграл
Применим метод
интегрирования замены переменной. Пусть
,
тогда
.
Найдём новые пределы интегрирования.
Найдём новые пределы интегрирования.
Если
,
то
;
если
,
то
.
С учётом введения новой переменной первоначальный интеграл примет вид:
.◄
2.4. Вычислить
определенный интеграл
.
Применим метод
интегрирования замены переменной. Пусть
,
тогда
,
.
Найдём новые пределы интегрирования.
Если
,
то
;
если
,
то
.
Тогда исходный интеграл примет вид:
.◄
2.5. Вычислить
определенный
интеграл:
Сделаем замену
переменных
.
Тогда
,
.
При этой замене пределы интегрирования
не изменятся. Тогда получим
2.6.
Вычислить определенный
интеграл:
Применим
универсальную тригонометрическую
подстановку
,
тогда
,
а пределами интегрирования будут
и
.
Получим
2.7.
Вычислить определенный
интеграл:
Применим
тригонометрическую подстановку
.
Тогда
,
пределы интегрирования
и
.
Тогда
.
3. Формула интегрирования по частям
Если каждая из
функций
и
имеет на отрезке
непрерывную производную, то справедлива
следующая формула
.
Примеры:
3.1. Вычислить
определенный
интеграл:
.
Так как подынтегральная функция чётная, то исходный интеграл примет вид:
.
Применим метод интегрирования по частям:
.
Пусть
;
тогда
.
Тогда первоначальный интеграл примет вид:
.
Применим ещё раз метод интегрирования по частям:
Пусть
;
тогда
.
Получаем:
.
Получили равенство:
.
Тогда:
.
Откуда:
.◄
3.2.
Вычислить определенный
интеграл:
.
Применим метод
интегрирования по частям. Пусть
.
Тогда
.
Первоначальный интеграл примет вид:
.◄
3.3.
Вычислить определенный
интеграл:
Применим метод интегрирования по частям. Пусть
.
Тогда
, 
.
Первоначальный интеграл примет вид:
.◄
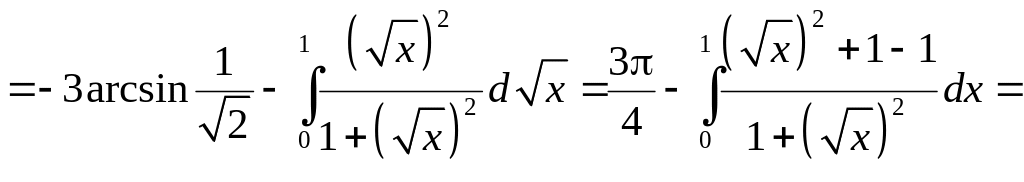
3.4. Вычислить
определенный
интеграл:
Применим метод интегрирования по частям. Пусть
.
Тогда
.
Получим:
.◄
3.5. Вычислить
определенный
интеграл:
Подынтегральная функция нечётная относительно синуса и косинуса. Применим универсальную тригонометрическую подстановку:
Пределы интегрирования:
.
С учётом подстановки первоначальный интеграл примет вид:
.
Теперь применим метод интегрирования по частям.
Пусть
.
Тогда
.
Получим:
.◄