4.5 Полігон швидкостей. Кінематичні коефіцієнти турбін
Завдяки тому, що полігон швидкостей безударного режиму будується за кутами нахилу лопатей, то змінюючи форму полігона, можна отримати різні типи турбін, які задовольняють тим чи іншим експлуатаційним вимогам. Форма полігона визначається кутами нахилу або відношеннями швидкостей (рис.4.7).
Чотири із співвідношень служать незалежними параметрами (кінематичними коефіцієнтами) лопатевої системи даного типу (див. рис. 4.7).
Коефіцієнт осьової швидкості (коефіцієнт витрати) дорівнює відношенню висоти полігона до верхньої основи
.
(4.9)
Для безударного режиму роботи турбіни можна записати
.
(4.10)
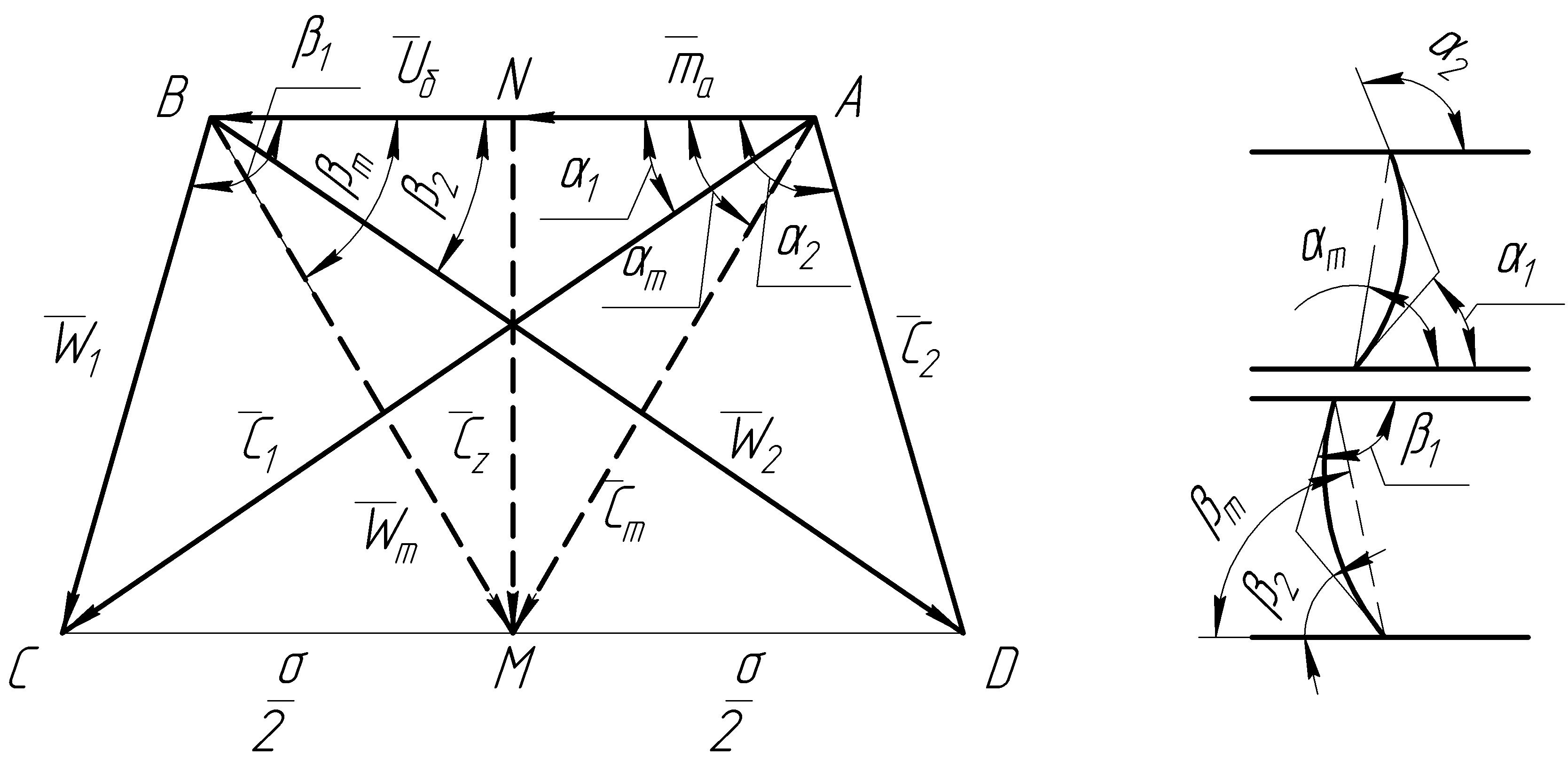
Рисунок 4.7 – Полігон швидкостей і побудова профілів лопатевої решітки за кінематичними коефіцієнтами
Із формули (4.10) видно, що зростанню коефіцієнта осьової швидкості відповідає зростання кутів нахилу середньо-векторних швидкостей і та кутів профілів лопатей.
При
заданих розмірах турбін коефіцієнт
характеризує співвідношення між витратою
рідини і частотою обертання на безударному
режимі. При однакових витратах рідини
більш тихохідною турбіною буде та, у
якої кути профілів більші. Якщо ж
швидкість обертання вала однакова, то
“багатолітражна” турбіна має більший
порівняно з “малолітражною”. Коефіцієнт
осьової швидкості знаходиться в межах
,
причому, якщо
1,
то це високошвидкісні (малолітражні
турбіни), коли
1
– низькошвидкісні (багатолітражні).
Коефіцієнт активності рівний відношенню тангенціальної проекції середньо-векторної абсолютної швидкості до колової швидкості
.
(4.11)
Коефіцієнт реактивності рівний відношенню тангенціальної проекції середньо-векторної відносної швидкості до колової швидкості
.
(4.12)
Причому
.
(4.13)
Коефіцієнти
і
служать показником неоднаковості потоку
в статорі і роторі. При
,
полігон швидкостей симетричний, а
решітки статора і ротора однакові як
оригінал і його дзеркальне відображення
(рис.4.7). В таких симетричних решітках
потік рідини в статорі і роторі однаковий,
тобто
;
;
.
Крім цього
і
.
Умова одночасного безударного входу в
статор і ротор виконується автоматично.
Трикутник середньо-векторних швидкостей
в симетричних решітках рівнобедрений.
Рівність
означає, що відносно однойменних точок
профілів рідина рухається в статорі і
роторі з однаковою швидкістю (це викликає
однакове зношування лопатей) і
забезпечується рівність перепадів
тиску в статорі
і в роторі
(загальний перепад тиску ділиться в
ступені навпіл).
При
0,5
решітки (а значить і відповідні турбіни)
називаються активними, а при
0,5
– реактивними. Гідромеханічне навантаження
(відносні швидкості, перепади тиску)
статора інтенсивніші в активних турбінах,
а ротора – в реактивних. Окремий випадок
відноситься до чисто активних решіток.
Трикутник середньо-векторних швидкостей
прямокутний, причому вектор
–
вертикальний. Тиск рідини по довжині
каналів в ступені ротора залишається
незмінним (
),
тому, що значення швидкості
не змінюється. Весь перепад тиску
відбувається у статорі.
Випадок,
коли
і
,
відноситься до чисто реактивних решіток.
Тиск рідини в статорі постійний (
),
весь перепад тиску приходиться на ротор.
Чисто реактивні турбіни в практиці не
використовують.
За заданими кутами лопатей коефіцієнт активності можна визначити за формулою
.
(4.14)
Коефіцієнт циркуляції – відношення нижньої основи полігона швидкостей до верхньої
.
(4.15)
Коефіцієнт
циркуляції характеризує відношення
між силовим (М)
і швидкісним ()
факторами в безударному режимі. В
залежності від значення
розрізняють три типи турбін: нормальні
(
),
високоциркулятивні (
)
і низькоциркулятивні (
).
Форму
профілів лопатей, що відповідають
величині кінематичних коефіцієнтів
можна представити, якщо побудувати
полігон безрозмірних швидкостей
(рис.4.7). Для цього від початку вектора
,
довільну величину якого приймемо за
одиницю, в тому ж напрямку відкладемо
відрізок довжиною
,
а потім перпендикулярний до нього
відрізок
.
З’єднавши кінці вектора
з кінцем відрізка
,
отримаємо трикутник середніх швидкостей.
Відкладемо в обидві сторони від його
вершин половину
і з’єднаємо кінці отриманих таким чином
відрізків з кінцями вектора
.
Тепер всі кути нахилу лопатей статора
і ротора визначені графічно. Дальше під
кутами
і
нанесемо на ескіз решітки хорди профілів.
Із кінців хорди під кутами
і
(для статора) і
і
(для ротора) проведемо дотичні до кінців
середніх ліній профілів, приблизні
контури яких легко відновити за напрямом
дотичних.
Кожному із значень коефіцієнтів , , і відповідає певний тип решіток і, навпаки, кожний тип решітки характеризується чотирма числами.
На
рис.4.8 представлена класифікація
турбінних решіток (для випадку коли
і
),
а змінюється тільки коефіцієнт активності.
Полігон швидкостей має форму паралелограма,
направленого в одну або іншу сторони в
залежності від коефіцієнта активності.
В окремому випадку при
полігон прямокутний.
Високоциркуляційні решітки (в яких ) мають полігон швидкостей, який звужується до верху. У випадку лопаті в роторі і статорі стануть більш пологими. Це сприяє зменшенню гідравлічних втрат при повертанні струминки в каналі.
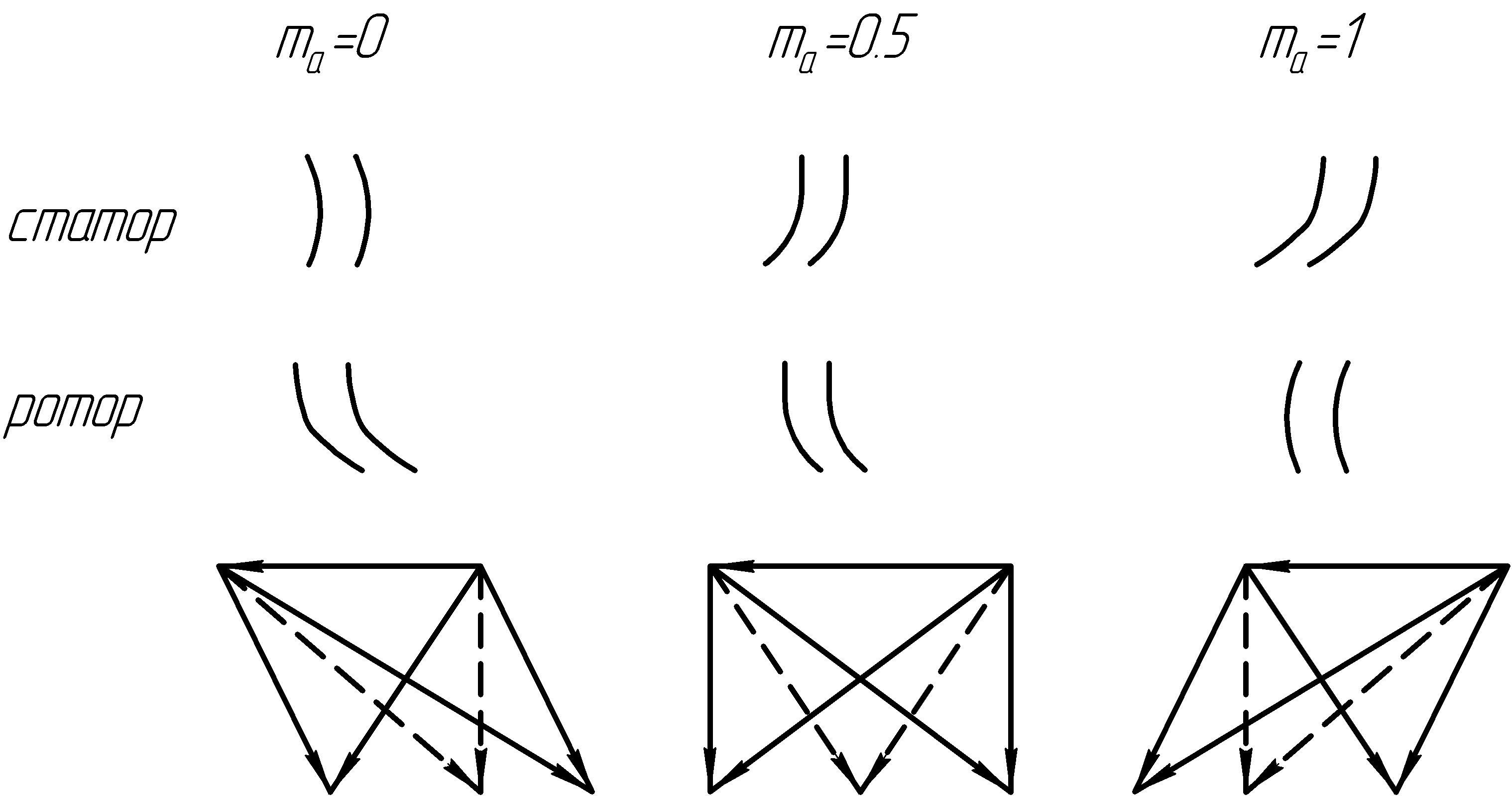
Рисунок 4.8 – Профілі турбінних решіток і вигляд полігонів швидкостей (при σ = 1 і = 0,9)