51. Простейшие свойства интеграла.

Пусть f интегрируема в смысле Н-Л на Р. Тогда:

1. правило перестановки пределов интегрирования:

Для любых а и в внутри Р

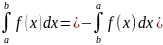
и

2. аддитивность интегралов относительно пределов интегрирования:

Для любых а, в, с внутри Р

3. правило дифференцирования интеграла по верхнему пределу интегрирования:

Для любых х внутри Р

4. теорема о среднем для интегралов:

Для любых а и в внутри Р найдется точка с, лежащая строго между а и в такая, что

52.Формулы замены переменной и интегрирование по частям

В некоторых случаях нахождение интеграла упрощается при переходе к другой переменной интегрирования. При этом если исходная и новая переменные и 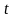связаны соотношением , где - обратимая дифференцируемая функция, то для интегралов справедливо равенство

,

в правой части которого после вычисления интеграла следует сделать обратную замену .

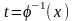В частности, используя замену (или ), получаем формулу

,

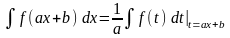позволяющую обобщить табличные интегралы. Например:

( ),

,

,

где 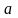и - произвольные постоянные, .

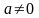Интегрирую выражение любого дифференциала произведения, получим:

53. Обобщенная теорема о реднем и формула конечных приращений Коши.

F, G непрерывны на , дифференцируемы на , для любого х, принадлежащего 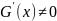, тогда найдется точка с, принадлежащая такая, что

Т еорема Коши: Пусть функции у=f(х) и у=g(х) неперырвны на отрезке [a,b],дифференцируемы хотя бы в открытом промежутке (a,b) и на этом промежутке g'(х) не обращается в нуль. Тогда существует такая точка c  (a,b), что выполняется равенство (1)

Докозательство: Вначале отметим, что знаменатель g(b)-g(a) ≠ 0,т.к. из равенства g(b)=g(a) следовало бы по теореме Ролля, что производная g'(х) обратилась бы в нуль в какой-нибудь точке промежутка (a,b), что противоречит условию g'(х)≠0. Образуем вспомогательную функцию:

К ней применима теорема Ролля: F(х) непрерывна в [a,b] и дифференцируема в (a,b) как сумма функций, непрерывных и дифференцируемых в соответствующих промежутках, кроме того, как легко проверить непосредственно, F(a)=F(b)=0. Следовательно, существует точка c  (a,b), , такая, что F'(c)=0. Вычисляем:

Подставляем x=c:

После деления на g'(х) (причем как говорилось раньше g'(х) 0), мы приходим к формуле (1)

54. Правила Лопиталя раскрытия неопределенностей.

Пусть и дифференцируемы на

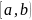
для любого х из

или ∞

Существует

Тогда существует

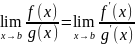
57. Непрерывность, дифференцируемость и интегрируемость предела функциональной последовательности.

Теорема 6 О непрерывности предела функц посл.

непрерывна в точке

=> f непрерывна в точке

Теорема 7 О дифференцируемости.

дифференцируема в точке

=>

=> , f дифференцируема в точке и

Следствие.

Теорема об интегрируемости предела.

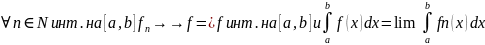
Теорема о дифференцируемости предела на интервале.