48. Теоремы Роля и Лагранжа.
Теорема Роля.
Пусть ф-ция f(x) удовл. сл. усл.
А)Непрерывна на [a,b]
Б) Дифференц. на (a,b)
В) принимает на коцах отрезков равные значения f(a)=f(b), тогда на (a,b) т-ка такая что f‘(c)=0, т.е. с-крит. т-ка.
Док-во. Р-рим сначала, тривиальный случай, f(x) постоянная на [a,b] (f(a)=f(b)), тогда f‘(x)=0 x (a,b), любую т-ку можно взять в кач-ве с. Пусть f const на [a,b], т.к. она непрер. на этом отрезке, то по т-ме Вейерштрасса она достигает своего экстрем. на этом отрезке и max и min. Поскольку f принимает равные знач. в гранич. т-ках, то хотя бы 1- экстр. – max или min обязательно достигается во внутр. т-ке. с(a,b) (в противном случае f=const), то по т-ме Ферма, тогда f‘(c)=0, что и требовалось д-ть.
Теорема Лагранжа.
непрерывна
на
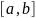и дифференцируема на
,
тогда найдется точка с, принадлежащая
такая, что
(формула конечных приращений)
Пусть ф-ция f(x) непрер. на отрезке [a,b] и диф. на интервале (a,b), тогда т. х и x+x [a,b] т-ка С лежащая между х и х+х такая что спаведлива ф-ла (f(x+x)-f(x))=f(c)x (7) => при сравнении с ф-лой приращения ф-ций с диф. заметим, что (7) явл. точной ф-лой, однако теперь пр-ная фолжна считаться в некоторой средней т-ке С «алгоритм» выбора которой неизвестен. Крайнее значение (a,b) не запрещены.
Придадим ф-ле (7) классический вид => x=a x+x=b+> тогда ф-ла (7)=(f(b)-f(a))/(b-a)=f‘(c) (7‘) – ф-ла конечных приращений Логранджа.
(f(b)-f(a))/(b-a)=f‘(c) (1)
Док-во сводится к сведению к т-ме Ролля. Р-рим вспом. ф-цию g(x)=f(x)-f(a)-(f(b)-f(a))/(b-a) (x-a)
Пусть ф-ция g(x) удовл. всем усл. т-мы Ролля на [a,b]
А)Непрерывна на [a,b]
Б) Дифференц. на (a,b)
В) g(a)=g(b)=0
Все усл. Ролля соблюдены, поэтому т-ка С на (a,b) g‘(c)=0 g‘(c)=f‘(x)-(f(b)-f(a))/(b-a). Ф-ла (1) наз-ся ф-лой конечных приращений.
49. Первообразная. Теорема о первообразной.
-
промежуток Р.
Св-во выполняется внутри промежутка, значит оно выполняется во внутренних точках промежутка.
Первообразная.
Пусть F определена на промежутке Р и f – внутри Р.
F
– первообразная f
на Р тогда и только тогда, когда F
непрерывна на Р и для любого х внутри Р
функция F
имеет производную и
Теорема о первообразных.
1. F – первообразная f на Р, тогда для любого С из множества действительных чисел F+C – первообразная f на Р.
2.
– первообразные f
на Р. Тогда найдется С из множества
действительных чисел такое, что
Доказательство: т.к. F1 и F2 по условию первообразные, то имеет место два равенства:
F1'(x) = f(x)
F2'(x) = f(x)
Обозначим F1(x) - F2(x) = φ(x), продифференцируем последнее равенство, используя два неравенства: F1'(x) - F2'(x) = f(x) - f(x) = 0.
Т.о. φ'(x) = 0, видно, что функция φ(x) постоянна, воспользуемся теоремой Лагранжа для φ(x), х[a,b]: φ(x) - φ(a) = φ'(ξ)(x - a) x<ξ<a
Т.к. φ(x) - φ(a) = 0 → φ(x) = φ(a) в любой точке промежутка Х, то φ(а) = С - постоянная, получаем, что F1(x) - F2(x) = C, теорема доказана.
50. Интегрируемость в смысле Ньютона – Лейбница и интеграл Ньютона - Лейбница.
Пусть f определена внутри промежутка Р.
f интегрируема в смысле Ньютона – Лейбница на Р тогда и только тогда, когда у f на Р существует первообразная.
Пусть f интегрируема в смысле Ньютона – Лейбница на Р и a принадлежит Р
,
где F
– первообразная f
и F(a)
= 0
(интегралом Н-Л с фиксированным нижним пределом а и переменным верхним пределом х от функции f назовем ту первообразную, которая в точке а обращается в 0)
Значение этой первообразной в точке в мы назовем:
,
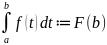где
F(a) = 0
Формула Н-Л
Пусть F – первообразная f на Р, тогда для любых а и в внутри Р:
Замечание.
Док-во.
x
a
F(x) – некот. первообразная для f(x)Ф(х) = ∫ f(t)dt также первообразная.
x
a
Ф'(x) = f(x), но две любые первообразные отличаются на постоянные согласные т.е. ∫ f(t)dt = F(x) + C1П
x
a
оложим х=а, тогда С1 = F(a)Cлед-но ∫ f(x)dx = F(x) - F(a)
b
a
Положим x=b, тогда ∫ f(t)dt = F(b) - F(a)
Что и требовалось доказать