26.Непрерывность функции в точке.Определение гейне и коши, их равносильность

Опр. (по Гейне; на языке последовательностей) Пусть точка х₀  D(f), f непрерывна в точке х₀ 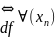: 1) , ; 2) ; для любой такой последовательности выполняется условие f(x_n) f(x₀).

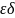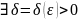
Опр. (по Коши; на языке ) Пусть х₀  D(f), f непрерывна в точке х₀ (|x-x₀|< .

1*) Пусть

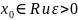
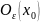называют интервал

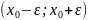
Эпс. окресности точки

2*) Пусть X c R ,

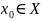
- внутренняя точка X <=>

3*) Множество Х с R открытое множество <=> все его точки внутренние.

4*) Точка - предельная точка множества X <=> в любой найдется

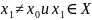
5*) Точка - изолированная точка <=> - не является предельной, т.е. 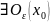в которой кроме точек из Х нет.

6*) X - замкнутое множество <=> X содержит все свои предельные точки.

27.Арифметические действия над непрерывными функциями

Th Пусть ф-ии f(x) и g(x) непрерывны в точке х0. Тогда ф-ии f(x)±g(x), f(x)g(x),f(x)\g(x) также непрерывны в этой точке(для частно g(x0)≠0)

Докво. Т.к. ф-ия f(x) непрерывна в точке х0, то lim(x->x0)(g(x))=g(x0). Тогда по теореме о пределах ф-ии пределы ф-ии f(x)+g(x),f(x)g(x) b f(x)\g(x) существуют и соответственно равны f(x0)±g(x0),f(x0)g(x0),f(x0)\g(x0)(g(x0)≠0).Но эти величины равны соответствующим значениям ф-ии в точке х0.Следовательно, согласно определению ф-ии f(x)±g(x),f(x)g(x),f(x)\g(x) непрерывны в точке х0

28.Непрерывность композиции

Пусть функция (t) непрерывна в точке t₀ и функция f(x) непрерывна в точке х₀=(t₀). Тогда функция f((t)) непрерывна в точке t₀.

Доказательство.

Для доказательства этой теоремы воспользуемся формальным преобразованием двух строчек кванторов. Имеем

Выписывая подчеркнутые кванторы, получим, что

,

что и говорит о том, что f((t)) непрерывна в точке t₀. 

Обратите внимание на следующие детали:

а) т.к. x=(t), то |(t)-(t₀)|< может быть записано как |x-x₀|<, и f(x) превращается в F((t));

б) при определении непрерывности (t) в точке t₀ в первом кванторе стоит буква . Это необходимо для согласования с квантором в предыдущей строке и взаимного уничтожения . Любая другая буква на этом месте не дала бы верного результата.

29.Локальная ограниченность непрерывной в точке функции

 25 Теорема 7.1. (о локальной ограниченности непрерывной функции)

Если f(x) непрерывна в точке a, то существует окрестность точки a, в которой f(x) ограничена.

Доказательство. Зададим какое-нибудь e > 0, например, e = 1. По определению непрерывности, $ d > 0: ½f(x) - f(a)½< e при ½x - a½< d, или < f(x) < в d-окрестности точки a. Это и означает, что f(x) ограничена в d-окрестности точки a.Т.док.

30.Устойчивость неравенств для непрерывной в точке функции

31.Предел функции в точке. Критерий Коши сходимости функции в точке.

Опр. (Гейне) Пусть f: RR, точка х₀ – предельная точка D(f), AR; А=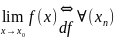 : 1) , , 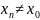; 2) , выполняется условие f(x_n)A.

Опр. (Коши) А= (0<|x-x₀|< (т.е. ).

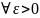
f сходится в точке х₀ 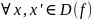((0 < |x-x₀|<