11.Числовой ряд, сумма ряда, сходящийся числовой ряд. Критерий Коши сходимости числового ряда.
Числовой ряд – бесконечная сумма членов бесконечной последовательности.
Сумма ряда – предел частичных сумм, если он существует и конечен.
Ряд называется сходящимся, если его сумма конечна.
Критерий
Коши
сходится
(лист
24)
12.Необходимое условие сходимости числового ряда.
Теорема: Пусть числовой ряд
u1+u2+...+un+... , (1)
сходится, а S - его сумма. Тогда при неограниченном возрастании числа n членов ряда его общий член un стремится к нулю Доказательство. Из условия теоремы имеем
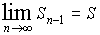
Так как
Sn - Sn-1 = un
то
Следует отметить, что этот признак является лишь необходимым, но не достаточным признаком сходимости ряда, так как можно указать ряд, для которого выполняется равенство
,
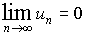а он, однако не является сходящимся
13.Абсолютная сходимость числовых рядов, связь со сходимостью. Критерий абсолютной сходимости.
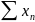абсолютно
сходится
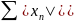- сходится
Теорема о сходимости абсолютно сходящегося ряда
Если абсолютно сходится, то - сходится
14.Основной признак Вейерштрасса.
Пусть
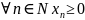- сходится
=
15 .Признак мажорации и признак сравнения.
-
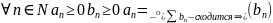
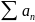сходится
и
ведут себя одинаково
16.Признак Коши.
Пусть
(верхний предел) тогда 1)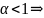
- сходится
2)
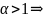- расходится 3)
17.Признак Даламбера.
Пусть
тогда 1)
- сходится
2) - расходится 3)
Пусть l - предел отношения последующего члена un+1 ряда (1) к предидущему un при n , т.е.
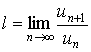
Тогда, если l<1, то ряд l сходится, если l > 1, то ряд l расходится, Если же l = 1, то вопрос о сходимости ряда (1) остается открытым. Доказательство. Согласно определению предела переменной величины, равенство
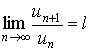
означает, что, начиная с некоторого номера n, выполняются неравенства
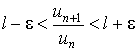
где e - наперед заданное сколь угодно малое положительное число. Рассмотрим три случая: а) пусть l < 1 . Тогда всегда можно взять e настолько малым, чтобы выполнялось неравенство
l + < 1
и, начиная с некоторого n , неравенство
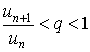
где q = l + , в силу чего (см. теорему 1) ряд (1) будет сходящимся; б) пусть l > 1 . Выбираем e так, чтобы
= l - 1 > 0
Тогда l - = 1 и
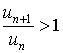
т.е. ряд (1) расходится (см. теорему 1) в) пусть l = 1 . Тогда ряд (1) может быть как сходящимся, так и расходящимся.
18. Теорема коши для рядов с убывающей последовательностью членов
Теорема. Для любого n принадлежашего множеству натур чисел при условии 0<=an+1<=an
Если ряд an сходится то ряд 2na2n тоже сходится
20.Признак Абеля.
1)(
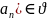(N)
2)
-сходится
– сходится
Пусть дан ряд:
: 
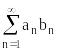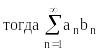сходится
Доказательство.
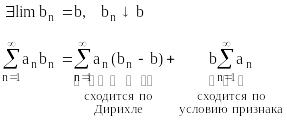Доказано.
21.Признаки Дирихле и Лейбница.
1)(
(N)
и
=
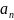2)
=
- сходится
если
члены знакочередующегося ряда
монотонно
убывают и стремятся к нулю то ряд
сходится
Пусть дан знакочередующийся ряд
(монотонно
стремится к 0), тогда А сходится.
Доказательство.
Т.к.
.
,
,
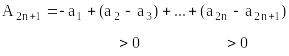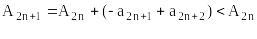то есть последовательность частичных
сумм
убывает, а
возрастает.
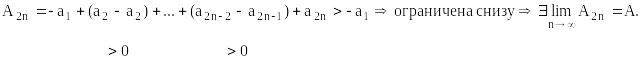Каждая
из последовательностей
ограничена и
.
Следовательно,
.
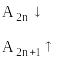
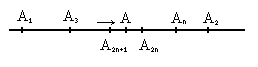
Заметим, что:
.
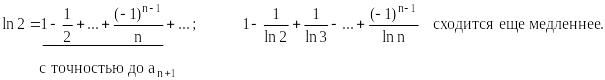
22.Сочетательный закон для числовых рядов.
-сходится
, (
-возрастающая
последовательность натуральных чисел,
=1
(2) сходится и суммы (1) и (2) равны
23 Коммутативный закон для абсолютно сходящихся рядов.
– абсолютно
сходится
любая его перестановка
– абсолютно сходится и
=
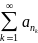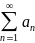
24.Теорема Римана и понятие условно сходящегося ряда.
Если ряд сходится, но не сходится абсолютно, то говорят, что ряд сходится условно.
сходится
условно
перестановка
=А
25.Перемножение абсолютно сходящихся рядов.
Если
и
абсолютно сходятся, то
при любой нумерации элементов матрицы
абсолютно сходится и его сумма равна
произведению сумм
и