7.Монотонные последовательности. Теорема Вейерштрасса о монотонных последовательностях.

( ) – неубывающая (невозрастающая) последовательность (монотонная)

( ) – возрастающая (убывающая) последовательность 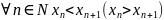(строго монотонная)

= и ( ) – монотонная причем, если неубывающая, то = sup (под sup написано )

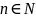если невозрастающая, то = inf (под inf написано )

Теорема (Вейерштрасс). Любая монотонная ограниченная последовательность имеет предел.

Доказательство. Докажем теорему для монотонной возрастающей последовательности  . Докажем, что точная верхняя граница для последовательности   и будет ее пределом.

Действительно, по определению точной верхней границы

Кроме того, какое бы ни взять число  , найдется такой номер  , что

Так как последовательность монотонна, то при   будет  , а значит, и   и выполняются неравенства

откуда и следует, что  .

8.Частичные пределы последовательности. Теорема Больцано – Вейерштрасса.

Число а называется частичным пределом последовательности , если найдется подпоследовательность, которая сходится к этому числу. 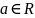- частичный предел ( ), ( ) a

Теорема Больцано-Вейерштрасса.У любой ограниченной последовательности найдется сходящаяся подпоследовательность. = ( )-сходящаяся.

Д-во:

Пользуясь теоремой (у всякой последовательности найдется монотонная подпоследовательность) получим

( )-монотонная. , т.к. Теор. Вейерштрасса о монотонных послед. )-сходится

9.Верхний и нижний пределы последовательности, связь со сходимостью.

Пусть = , тогда верхний предел определяется пределом верхней грани; нижний – нижней.

Теорема. Пусть Хn – 0 с чертой внизу (1) . (Хn) сходится когда верхний предел=нижнему пределу=А, причем предел тоже равен А.

10.Фундаментальные последовательности и критерий Коши сходимости последовательности.

Опр.( ) – фундаментальна

Критерий Коши: ( ) сходится ( ) фундаментальна

Доказательство.

1. Необходимость. Пусть =a. Зададим произв.  > 0.

По определению предела,  N,  n > N:x_n-a < , и  m > N:x_m-a < . Если n > N, m > N, то x_m-x_n=(x_m-a) - (x_n-a) + < .

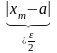Это и означает по определению, что последовательность {x_n} - фундаментальная. Необходимость доказана.

2. Достаточность. последовательность {x_n} ограничена, следовательно, можно выделить сходящуюся подпоследовательност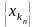ь . Пусть = a. Докажем, что = a. Зададим произвольное  > 0. Так как подпоследовательность сходится к a, начиная с некоторого номера N₁ все члены  { - окрестности точки a}, а так как последовательность {x_n} - фундаментальная, то начиная с некоторого номера N₂ все члены x_n отстоят от членов 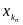меньше, чем на . Следовательно, начиная с номера N = max (N₁, N₂) все члены последовательности x_n  {- окрестности точки a}, а это и означает, что = a, что и требовалось доказать. Теорема доказана.