58. Приближение непрерывной функции ломаными. Интегрируемость в смысле Ньютона-Лейбница непрерывной функции.

Функция, графиком которой является ломаная с вершиной 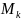называют ломаной.

Теорема о приближении непрерывной функции ломаными.

Если f непрерывна на [a,b] =>

Теорема об интегрируемости непрерывной функции.

Если f непрерывна на [a,b] , то f интегрируема на [a,b]

59. Определение n-производной и n-интеграла.

Опр.

Пусть f дифференцируема на промежутке P ( т.е. f диф ),

тогда f ' определена на P и

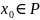
f- 2-дифференцируема в Т <=> f ' диф. в Т. и

f- 2-диф . на P <=> f-2 диф

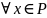
Опр.

f-1диф. на P <=> f диф. на P и

Пусть определено понятие (n-1)-дифференцируемости на P

при n>1 и

f - n-дифференцируема на промежутке Р <=> функция дифференцируема на P и

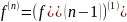
Опр.

Пусть f интегрируема в смысле Ньютона-Лейбница на промежутке P,

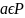
1-интегралом

Пусть определен (n-1) интеграл, n>1

тогда n-интеграл:

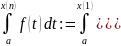
60. Формула Тейлора, как обобщение формулы Ньютона-Лейбница.

Теорема:Формула Тейлора, как обобщение формулы Ньютона-Лейбница.

f - n-дифференцируема на Р, =>

=>

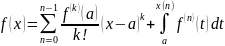
Доказательство по методу математической индукции.

61. Формула Тейлора с остаточным членом в интегральной форме. Формы Шлемильха-Роша, Коши и Лагранжа остаточного члена формулы Тейлора.

Теорема 3. Остаточная формула Тейлора.

-диф на Р =>

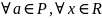
Теорема 4. Формула Тейлора с остаточным членом в форме Шлемильха-Роша.

-диф на Р =>

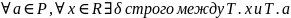
Cледствие. ( Ост Лагранжа)

Следствие 2. (Форма Коши)

62. Формула Тейлора с остаточным членом в форме Пеано.

f-n диф. в Т.а => ,при

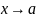
63. Достаточное условие локального экстремума.

f- n диф. в Т. , Т. - внутри D(f)

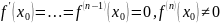
Тогда, если n четное, то

1) 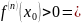Т. - точка локального минимума.

2) Т. - точка локального максимума.

Если n- нечетное, то

1) Т. - точка роста.

2) Т. - точка убывания.

64. Выпуклые функции, дифференциальные св-ва выпуклых ф-ий

Опр. Ф-ция явл. выпуклой (вогнутой) на (a,b) если кассат. к граф-ку ф-ции в любой т-ке интервала, лежит ниже (выше) гр. ф-ции.

y=y0+f‘(x0)(x-x0)=f(x0)+f‘(x0)(x-x0) – линейная ф-ция х, который не превосходит f(x) и не меньше f(x) в случае вогнутости неравенства хар-щие выпуклость (вогнутость) через диф. f(x)f(x0)+ f‘(x0)(x-x0)  x,x0(a;b) f вогнута на (а,b). Хорда выше (ниже), чем график для вып. ф-ций (вогн.) линейная ф-ция kx+b, в частности постоянна, явл. вып. и вогнутой.

f- выпуклая на (a,b) <=> множество точек располагающихся выше(ниже) графика есть выпуклое(вогнутое) множество.

65. Критерий выпуклости дифференцируемой функции.

Пусть f дифференцируема на (a,b) => f выпуклая <=> f ' неубывает и сходится

66. Критерий выпуклости дважды дифференцируемой функции.

Пусть f - 2диф на (a,b), тогда f-выпуклая <=>