
- •1.Равномощные множества. Счетные множества и их свойства.
- •2 . Верхняя и нижняя грани числовых множеств. Теорема о существовании верхней грани. Несчетность множества действительных чисел.
- •3.Ограниченные и бесконечно малые последовательности.Действия над ними
- •4 . Предел последовательности, единственность предела.
- •5.Арифметические действия над сходящимися последовательностями
- •6 .Порядковые свойства предела и порядковый признак существования предела.
- •7.Монотонные последовательности. Теорема Вейерштрасса о монотонных последовательностях.
- •8.Частичные пределы последовательности. Теорема Больцано – Вейерштрасса.
- •9.Верхний и нижний пределы последовательности, связь со сходимостью.
- •10.Фундаментальные последовательности и критерий Коши сходимости последовательности.
- •11.Числовой ряд, сумма ряда, сходящийся числовой ряд. Критерий Коши сходимости числового ряда.
- •12.Необходимое условие сходимости числового ряда.
- •18. Теорема коши для рядов с убывающей последовательностью членов
- •20.Признак Абеля.
- •21.Признаки Дирихле и Лейбница.
- •26.Непрерывность функции в точке.Определение гейне и коши, их равносильность
- •27.Арифметические действия над непрерывными функциями
- •28.Непрерывность композиции
- •29.Локальная ограниченность непрерывной в точке функции
- •30.Устойчивость неравенств для непрерывной в точке функции
- •31.Предел функции в точке. Критерий Коши сходимости функции в точке.
- •32.Свойства предела.
- •33.Порядковый признак существования предела.
- •34.Односторонняя непрерывность функции и односторонние пределы функции в точке. Точки разрыва функции и их классификация.
- •35.Монотонные функции и их свойства.
- •36.Компактное числовое множество. Критерий компактности.
- •37.Теорема о непрерывном образе компакта. Две теоремы Вейерштрасса о непрерывных функциях.
- •38.Теорема Коши о промежуточных значениях непрерывной функции.
- •40.Равномерная непрерывность функции на множестве. Теорема Кантора.
- •41. Дифференцируемость функции в точке, производная функции в точке. Геометрический и физический смысл производной.
- •42.Непрерывность дифференцируемой функции
- •43.Дифференцируемости композиций
- •44. Арифметические действия над дифференцируемыми функциями
- •47. Локальный экстремум и теорема Ферма.
- •48. Теоремы Роля и Лагранжа.
- •49. Первообразная. Теорема о первообразной.
- •50. Интегрируемость в смысле Ньютона – Лейбница и интеграл Ньютона - Лейбница.
- •51. Простейшие свойства интеграла.
- •52.Формулы замены переменной и интегрирование по частям
- •53. Обобщенная теорема о реднем и формула конечных приращений Коши.
- •54. Правила Лопиталя раскрытия неопределенностей.
- •57. Непрерывность, дифференцируемость и интегрируемость предела функциональной последовательности.
- •58. Приближение непрерывной функции ломаными. Интегрируемость в смысле Ньютона-Лейбница непрерывной функции.
- •59. Определение n-производной и n-интеграла.
- •65. Критерий выпуклости дифференцируемой функции.
- •66. Критерий выпуклости дважды дифференцируемой функции.
1.Равномощные множества. Счетные множества и их свойства.
Множество
Х равномощно ( )
множеству У, если существуют взаимно
однозначные отображения Х на У.
)
множеству У, если существуют взаимно
однозначные отображения Х на У.
Множество, равномощное множеству натуральных чисел, называют счетным.
Если
 х
х Х
ставится в соответствие единственный
элемент y,
y
Х
ставится в соответствие единственный
элемент y,
y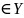 ,
то говорят, что дано отображение множества
Х на У(функция).
,
то говорят, что дано отображение множества
Х на У(функция).
Теорема 1. множество содержит счетное подмножество.
Док-во.
Выберем элемент a1A (A не пусто, так как оно бесконечно);
выберем элемент a2A\{a1} (A\{a1} не пусто, так как A бесконечно);
и т.д. В результате получим множество, каждому элементу которого сопоставлено натуральное число n.
Всякое бесконечное подмножество счетного множества является счетным или конечным множеством
Теорема 2. подмножество B счетного множества A счетно.
Д-во. Согласно Т1 из множества B можно выделить счетное C.
Тогда CBA. В силу определения мощности |C||B||A|. Так как A и C — счетные, то |A|=|C|. Т. е. |A||B||A|. Отсюда следует, что |B|=|A|.
Тем самым, счетное множество равномощно своей части.
(теорема
Кантора) пусть при
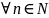 ,
,
 – счетное множество, Х=
– счетное множество, Х=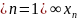 , то Х - счетное (счетное (или
конечное) объединение
счетных множеств является счетным
множеством)
, то Х - счетное (счетное (или
конечное) объединение
счетных множеств является счетным
множеством)
Доказательство. Пусть
A1={a11,a12,…},
A2={a21,a22,…},
A3={a31,a32,a33,…},
………………..
An={an1,an2,an3,…,ann,…},
………………..
Расположим элементы A в следующем порядке
a11,a12,a21,a31,a22, a13,a14,a23,a32,a41,…
Тем самым, получили взаимно однозначное отображение N на A.
Множество рациональных чисел счетно.
Любое подмножество счётного множества не более чем счётно (т.е. конечно или счётно).[1]
Объединение конечного или счётного числа счётных множеств счётно.[1]
Прямое произведение конечного числа счётных множеств счётно.
Множество всех конечных подмножеств счётного множества счётно.
Множество всех подмножеств счётного множества континуально и, в частности, не является счётным.
2 . Верхняя и нижняя грани числовых множеств. Теорема о существовании верхней грани. Несчетность множества действительных чисел.
Пусть Х={x} – ограниченное множество вещественных чисел. Число m=inf {x} называется нижней гранью множества Х, если :
Каждое
х
Х
(икс из множества икс большое) удовлетворяет
неравенству х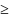 m;
m;
Какого
бы ни было
 >0,
существует х’
Х
такое, что х’<m+
,
>0,
существует х’
Х
такое, что х’<m+
,
Аналогично число М=sup{x} называется верхней гранью множества Х, если :
Каждое
х
Х
(икс из множества икс большое) удовлетворяет
неравенству х ;
;
Для любого >0, существует x” Х такое, что х’>M- .
---------------------------------------------------
Пусть
X R
(Х – подмножество действительных чисел)
и
R
(Х – подмножество действительных чисел)
и
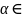 R.
Тогда
R.
Тогда
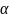 -
мажоранта Х, если
х
Х,
х
-
мажоранта Х, если
х
Х,
х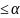 ;
;
-
миноранта Х, если
х
Х,
х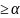 ;
;
Множество называют ограниченным сверху, если у него есть мажоранта, снизу – миноранта. Если ограниченно и сверху, и снизу, то просто ограниченным.
Пусть Х – множество, ограниченное сверху. Верхней гранью множества Х называют наименьшую мажоранту.(sup X)
Пусть Х – множество, ограниченное снизу. Нижней гранью множества Х называют наибольшую миноранту. (inf X)
------------------------------------------
Пусть
Х 0
(не пустое) и ограниченно сверху,
0
(не пустое) и ограниченно сверху,
 sup
X
(существует верхняя грань). (лист
4)
sup
X
(существует верхняя грань). (лист
4)
Множество х=(0,1) не является счетным множеством. (лист 9)
