
- •1.Определения и вычисление 2 и 3го порядка. Свойства определителей.
- •2.Матрицы,основные определения. Действия над матрицами.
- •3.Определение минора элемента, алгебраического дополнения.
- •4.Понятие обратной матрицы. Теорема об ее вычислении.
- •5.Понятие о ранге матрицы.
- •6.Системы линейных уравнений. Основные понятия.
- •7.Системы линейных однородных уравнений. Методы решения.
- •8.Правило Крамера.
- •Если система (2.3) имеет единственное решение, определяемое по формулам: .
- •9.Метод Гаусса.
- •10) Решение линейных систем с помощью обратной матрицы.
- •11)Векторы. Основные определения. Сложение и вычитание векторов.
- •12)Умножение вектора на скаляр. Коллинеарные вектора. Необходимое и достаточное условия коллинеарности векторов.
- •13)Определение проекции вектора на ось. Теоремы о проекциях. Вектор в трехмерном пространстве. Направляющие косинусы. Разложение вектора по ортам.
- •14) Линейная зависимость и независимость векторов.
- •15)Скалярное произведение векторов. Геометрический и механический смысл. Свойства. Таблица умножения ортов. Угол между векторами.
- •16)Понятие тройки векторов. Левая, правая тройка, Определение векторного произведения. Геометрический смысл. Свойства. Векторное произведение в декартовых координатах.
- •17) Смешанное произведение векторов. Свойства и геометрический смысл. Компланарные векторы.
- •18) Полярная система координат
- •19) Прямая на плоскости. Общее уравнение прямой. Частные случаи. Расположение двух прямых на плоскости.
- •20)Эллипс.
- •21)Гипербола.
- •22)Парабола.
- •23)Уравнение линии и поверхности в пространстве.
- •24)Плоскость. Общее уравнение. Случаи расположения 2-х плоскостей в пространстве. Уравнение плоскости, проходящей через 3 точки.
- •25.Уравнение прямой в пространстве. Случаи расположения двух прямых. Угол между прямой и плоскостью. Формула расстояния от точки до плоскости.
- •26. Поверхности второго порядка. Построение методом сечений.
- •27.Определение функции. Способы задания. Классификация.
- •28.Предел числовой последовательности. Основные определения. Теорема об ограниченной последовательности.
- •29. Основные теоремы о пределах.
- •30.Определение множества и ограниченного множества. Супремум. Инфимум.
- •Ограниченное числовое множество.
- •Ограниченное множество в метрическом пространстве
- •Ограниченность в частично упорядоченном множестве
- •31.Определение предела числовой последовательности. Признаки существования предела, теорема о зажатой последовательности.
- •32.Предел функции. Теоремы о пределах. Способы вычисления пределов.
- •Алгоритм решения.
- •33.Определение предела функции. 1 и 2 замечательный предел.
- •Бесконечно большие f(X) и g(X) считаются величинами одного порядка, если
- •Если , то f(X) считается бесконечно большой более высокого порядка, чем g(X).
- •Бесконечно большая f(X) называется величиной k-го порядка относительно бесконечно большой g(X), если .
- •35.Односторонние пределы функции. Определение. Непрерывность функции в точке.
- •36.Непрерывность функции в точке.
- •37.Понятие проивзодной,ее физический и геометрический смысл.
- •38. Определение производной. Правило дифференцирования суммы и частного функции, разности и произведения функций.
- •39.Правило дифференцирования сложной функции. Теорема о производной обратной функции. Дифференцирование функции, заданной неявно. Понятие логарифмической производной.
- •40.Нахождение производной функции, заданной параметрически.
- •41.Дифференциал. Определение ,свойства, геометрический смысл.
- •42.Дифференциалы и производные высших порядков.
- •43.Теоремы Ферма, Ролля, Лагранжа и Коши и их геометрический смысл.
- •44.Правило Лопиталя. Следствие о раскрытии неопределенностей разных видов.
- •45.Формула Тейлора.
- •46.Выпуклость и вогнутость кривых. Определение. Определение точки перегиба.
- •47.Асимпоты. Определение. Классификация.
- •48.Комплескные числа.
- •49.Функции нескольких переменных.
- •50.Предел функции двух переменных. Непрерывные функции, частные производные.
- •51.Полный дифференциал. Производные сложной функции.
- •52.Неявные функции и их дифференцирование.
- •53.Касательная плоскость и нормаль к поверхности. Частные производные.
- •54.Дифференциалы высших порядков.
- •55.Первообразная функция и неопределенный интеграл .Свойства неопределенного интеграла.
- •56.Интегрирование методом замены и внесения под знак дифференциала.
- •57.Интегрирование по частям.
- •58. Интегрирование рациональных функций.
- •59.Интегрирование иррациональных функций.
- •1. Сделаем замену , тогда , а . Следовательно,
- •2. . Так как , а , выберем в качестве новой переменной . Тогда . Поэтому
- •60.Интегрирование тригонометрических функций.
47.Асимпоты. Определение. Классификация.
Прямая называется асимптотой графика функции y = f(x) , если расстояние от переменой точки этого графика до прямой стремится к нулю при удалении точки в бесконечность.
Рассмотрим три вида асимптот и определим способы их нахождения.
Вертикальные асимптоты – прямые, задаваемые уравнениями вида х = а. В этом случае определение асимптоты подтверждается, если хотя бы один из односторонних пределов функции в точке а бесконечен. Пример. Вертикальной асимптотой графика функции y = 1/x является прямая х = 0, то есть ось ординат.
Горизонтальные асимптоты – прямые вида у = а. Такие асимптоты имеет график функции, предел которой при
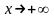 или при
или при
 конечен, т.е.
конечен, т.е.
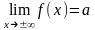 .
.Наклонные асимптоты – прямые вида y = kx + b. Найдем k и b. Поскольку при
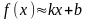 ,
,
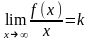 ,
если этот предел существует, конечен
и не равен нулю. Однако даже при выполнении
этих условий наклонная асимптота может
не существовать. Для ее существования
требуется, чтобы имелся конечный предел
при
разности
f(x)
– kx.
Этот предел будет равен b
, так как при
,
если этот предел существует, конечен
и не равен нулю. Однако даже при выполнении
этих условий наклонная асимптота может
не существовать. Для ее существования
требуется, чтобы имелся конечный предел
при
разности
f(x)
– kx.
Этот предел будет равен b
, так как при
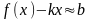 .
.
Замечание. Число вертикальных асимптот графика функции не ограничено, а наклонных и горизонтальных в сумме может быть не более двух (при и при ).
Примеры.
Функция y = tgx имеет разрывы 2-го рода при
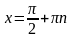 ,
причем односторонние пределы в этих
точках бесконечны. Следовательно,
- вертикальные асимптоты графика.
,
причем односторонние пределы в этих
точках бесконечны. Следовательно,
- вертикальные асимптоты графика.Функция
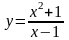 имеет бесконечный разрыв при х
= 1, то есть
х = 1
– вертикальная асимптота.
имеет бесконечный разрыв при х
= 1, то есть
х = 1
– вертикальная асимптота.
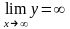 ,
поэтому горизонтальных асимптот график
не имеет. Проверим наличие наклонных
асимптот. Для этого вычислим
,
поэтому горизонтальных асимптот график
не имеет. Проверим наличие наклонных
асимптот. Для этого вычислим
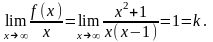 Тогда
Тогда
 Заметим, что оба предела не зависят от
знака бесконечности, поэтому прямая
y
= x
+ 1 является
асимптотой графика на обоих концах оси
Ox.
Заметим, что оба предела не зависят от
знака бесконечности, поэтому прямая
y
= x
+ 1 является
асимптотой графика на обоих концах оси
Ox.
48.Комплескные числа.
Комплексным числом z называется упорядоченная пара действительных чисел (а,b) : z = (a,b) (термин «упорядоченная» означает, что в записи комплексного числа важен порядок чисел а и b: (a,b)≠(b,a) ). При этом первое число а называется действительной частью комплексного числа z и обозначается a = Re z, а второе число b называется мнимой частью z: b = Im z.
Два комплексных числа z1 = (a1 , b1) и z2 = (a2 , b2 ) равны тогда и только тогда, когда у них равны действительные и мнимые части, то есть a1 = a2, b1 = b2.
Действия над комплексными числами.
1. Суммой комплексных чисел z1 = (a1 , b1) и z2 = (a2 , b2 ) называется комплексное число z = (a,b) такое, что a = a1 + a2 , b = b1 + b2 . Свойства сложения: а) z1 + z2 = z2 + z1; б) z1 + (z2 + z3 ) = (z1 + z2 ) + z3; в) существует комплексное число 0 = (0,0): z + 0 = z для любого комплексного числа z.
2. Произведением комплексных чисел z1 = (a1 , b1) и z2 = (a2 , b2 ) называется комплексное число z = (a,b) такое, что a = a1a2 – b1b2 , b = a1b2 + a2b1 . Свойства умножения: а) z1z2 = z2z1 ; б) z1 (z2 z3) = (z1 z2) z3, в) (z1 + z2) z3 = z1 z3 + z2 z3 .
Замечание. Подмножеством множества комплексных чисел является множество действительных чисел, определяемых как комплексные числа вида (а,0). Можно убедиться, что при этом определение операций над комплексными числами сохраняет известные правила соответствующих операций над действительными числами. Кроме того, действительное число 1 = (1,0) сохраняет свое свойство при умножении на любое комплексное число: 1∙ z = z.
Определение 7.3. Комплексное число (0, b) называется чисто мнимым . В частности, число (0,1) называют мнимой единицей и обозначают символом i.
Свойства мнимой единицы:
1) i∙i=i² = -1; 2) чисто мнимое число (0,b) можно представить как произведение действительного числа (b,0) и i : (b,0) = b∙i.
Следовательно, любое комплексное число z = (a,b) можно представить в виде: (a,b) = (a,0) + (0,b) = a + ib.
Определение 7.4. Запись вида z = a + ib называют алгебраической формой записи комплексного числа.
Замечание. Алгебраическая запись комплексных чисел позволяет производить операции над ними по обычным правилам алгебры.
Определение
7.5.
Комплексное число
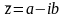 называется
комплексно
сопряженным
числу z
= a
+ ib.
называется
комплексно
сопряженным
числу z
= a
+ ib.
3. Вычитание комплексных чисел определяется как операция, обратная сложению: z =(a,b) называется разностью комплексных чисел z1 = (a1 , b1) и z2 = (a2 , b2 ), если a = a1 – a2 , b = b1 – b2.
4. Деление комплексных чисел определяется как операция, обратная умножению: число z = a + ib называется частным от деления z1 = a1 + ib1 и z2 = a2 + ib2 (z2 ≠ 0), если z1 = z∙z2. Следовательно, действительную и мнимую части частного можно найти из решения системы уравнений: a2 a – b2 b = a1 , b2 a + a2 b = b1.
