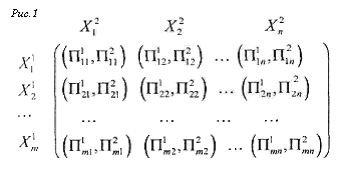3. Элементы теории игр Платежная матрица

Математическую дисциплину, исследующую ситуации, в которых принятие решения зависит от нескольких участников, называют теорией игр. Предметом теории игр являются такие ситуации, в которых важную роль играют конфликты и совместные действия.

В теории игр "лиц, принимающих решения", называют игроками, а целевую функцию - платежной функцией. Каждый игрок располагает конечным или бесконечным набором допустимых решений, называемых стратегиями. Выигрыш каждого игрока определяется его платежной функцией, значения которой зависят от стратегий всех участников игр.

Фактически игра представляет собой совокупность правил, известных всем игрокам. Эти правила, с одной стороны, определяют множества стратегий игроков, а с другой - последствия и выигрыши в результате выбора каждой из стратегий. Заметим, что в теории игр понятие стратегии является одним из центральных.

Классификацию игр проводят по различным признакам:

а) по числу игроков;

б) по числу стратегий;

в) по свойствам платежных функций;

г) по характеру предварительной договоренности между игроками.

Игру, в которой участвуют n игроков, называют игрой с п участниками. Количество п участников может быть равным 2, 3, и т.д. При наличии двух игроков могут возникать и конфликтные ситуации, и необходимость в координированных действиях (кооперация). Если в игре участвует не менее трех игроков, то могут создаваться коалиции, т.е. группы из двух или более игроков, имеющих общую цель и координирующих свои стратегии.

По количеству стратегий различают игры конечные и бесконечные. Если хотя бы один из игроков располагает бесконечным множеством стратегий, то игру взывают бесконечной. Если же каждый из игроков располагает конечным множеством стратегий, то игру называют конечной.

Еще один способ классификации игр - по свойствам платежной функции. В игре с нулевой суммой общая сумма выигрышей всех игроков равна нулю. В игре с нулевой суммой и двумя участниками выигрыш одного из них равен проигрышу другого. Таким образом, в играх с нулевой суммой существует конфликт между сроками, и поэтому их называют также антагонистическими играми. Прямой Противоположностью играм с нулевой суммой являются игры двух игроков с постоянной разностью, в которых оба игрока выигрывают или проигрывают одновременно. Поэтому игрокам выгодно действовать согласованно.

В зависимости от характера предварительной договоренности между игроками различают кооперативные и некооперативные игры. Игра кооперативная, если до ее начала игроки образуют коалиции и принимают взаимообязывающие соглашения о координации своих стратегий. В противном случае игра будет некооперативной.

Прежде чем переходить к рассмотрению основных способов описания и анализа любой конкретной игры, введем еще два понятия, широко используемых в теории игр.

Ход - это момент игры, когда игроки должны выбрать один из возможных вариантов действий, т.е. принять одно из допустимых решений.

Партия игры - это определенная совокупность ходов и выборов возможных вариантов действий.

Существуют два способа описания и анализа любой конкретной игры.

Первый способ предполагает следующее:

1. перечисление ходов, которые могут сделать игроки,

2. определение информации, которой располагают игроки в процессе игры;

3. определение возможных вариантов действий игроков;

4. указание предельных размеров платежей в конце игры.

Игру, описанную подобным образом, называют игрой в развернутой или экстенсивной форме, а само описание, как правило, составляют в виде дерева игры, аналогичного дереву решений. Игры в развернутой форме также называют позиционными играми.

Игру в развернутой форме называют игрой с полной информацией, если в ней нельзя делать одновременно несколько ходов, и если участникам известны выборы, сделанные при предшествующих ходах, включая и случайные ходы. Примером игры с полной информацией являются шахматы. Покер представляет собой игру_с неполной информацией, так как игрокам неизвестно, какие карты находятся на руках у противника.

Второй способ описания игры предполагает рассмотрение всех возможных стратегий каждого игрока и определение платежей, соответствующих любым возможным комбинациям стратегий всех игроков. Игру, описанную вторым способом, обычно называют игрой в нормальной форме.

Нормальная форма игры двух участников состоит из двух платежных матриц, содержащих суммы выигрышей и проигрышей каждого из игроков для любой из возможных пар стратегий. Обычно эти две матрицы объединяются в одну, как изображено на рис 1. Если первый игрок располагает множеством стратегий , а второй игрок - множеством стратегий , то на пересечении i-ой строки и j-ro столбца объединенной платежной матрицы находится пара чисел , представляющих собой выигрыши первого и второго игроков при выборе ими стратегий и соответственно.

Единая платежная матрица состоит из m строк и n столбцов, где m - число стратегий первого игрока, a n- второго (имеется в виду конечная игра). Считается, ч_То каждому из игроков известны все элементы единой платежной матрицы игры.