
- •Содержание
- •Раздел 1. Рабочая программа дисциплины
- •График учебного процесса
- •Самостоятельная работа
- •Раздел 2. Краткое содержание основных тем
- •1. Линейное и дискретное программирование
- •1.1. Модели линейного программирования
- •Геометрический метод решения задачи линейного программирования
- •Симплексный метод решения злп
- •Двойственные задачи
- •1. 2. Модели целочисленного линейного программирования
- •Методы отсечения
- •Метод ветвей и границ
- •1. 3. Транспортная задача Классическая транспортная задача
- •Симплексный метод решения задач транспортного типа (метод потенциалов)
- •2. Модели динамического программирования Динамическое программирование
- •3. Элементы теории игр Платежная матрица
- •Игры двух участников с нулевой суммой
- •Решение игр двух участников с нулевой суммой в смешанных стратегиях
- •Игры двух участников с ненулевой суммой
- •4. Элементы теории массового обслуживания Марковские процессы
- •Уравнения Колмогорова. Предельные вероятности состояний
- •Смо с отказами
- •Смо с ожиданием (очередью)
- •5. Сети Эйлеровы и гамильтоновы графы. Деревья
- •Минимальное порождающее дерево
- •Кратчайший маршрут
- •Максимальный поток
- •Сетевой график. Критический путь
- •6. Модель Леонтьева многоотраслевой экономики (дополнительно)
- •Раздел 3. Рекомендуемая литература
- •Раздел 4. Типовые расчеты
- •Раздел 5. Методические указания по выполнению типовых расчетов
- •1. В целях единообразного оформления типовых расчетов в орагс принят следующий титульный лист:
- •2. Вместо а подставьте третью справа цифру в номере зачетной книжки. Если по плану один типовой расчет, то произвольно выбираются 8 задач из предложенных 14.
- •Раздел 6. Практические и лабораторные работы
- •Раздел 7. Контроль знаний студентов
- •Отметка "незачтено"
Раздел 5. Методические указания по выполнению типовых расчетов
1. В целях единообразного оформления типовых расчетов в орагс принят следующий титульный лист:
ОРЛОВСКАЯ РЕГИОНАЛЬНАЯ АКАДЕМИЯ ГОСУДАРСТВЕННОЙ СЛУЖБЫ»
Тульский филиал ________________________________________________________________________
Факультет: «Государственное и муниципальное управление»
Кафедра: «Гуманитарных и социально-экономических дисциплин»
Факультет: «Государственное и муниципальное управления»
Кафедра: «Гуманитарных и социально-экономических дисциплин»
ТИПОВОЙ РАСЧЕТ
по дисциплине «Экономико-математические модели в управлении»
Выполнил Проверил
Студент 1 курса группы № 40 Руководитель (преподаватель)
Заочной формы обучения К. физ.-мат. наук, доцент И.В. Добрынина
Факультет ГМУ
Иванова Людмила Юрьевна Оценка (зачтено, не зачтено)
Дата, подпись Дата, подпись
Тула - 2010
2. Вместо а подставьте третью справа цифру в номере зачетной книжки. Если по плану один типовой расчет, то произвольно выбираются 8 задач из предложенных 14.
3. При оформлении задач типового расчета необходимо записать условие, экономико-математическую модель, решение задачи и ответ. При использовании Microsoft Ехсеl оформление может выглядеть следующим образом.
Задача. Организация арендует баржу грузоподъёмностью 200 т. На этой барже предполагается перевозить груз 4 типов. Вес и стоимость единицы груза соответственно равны 20, 15, 20, 14 и 100, 80, 40, 30. Необходимо погрузить на баржу груз максимальной стоимости.
Экономико-математическая модель:
Пусть xj (j=1,2,3,4) – число предметов j-го типа, которое следует погрузить на баржу. Тогда ЭММ задачи запишется следующим образом:
max f(x1, x2, x3, x4) =100x1+80x2+40x3+30x4, 20x1+15x2+20x3+14x4 ≤ 200, xj (j=1, 2, 3, 4) – целые неотрицательные.
Решение.
1.
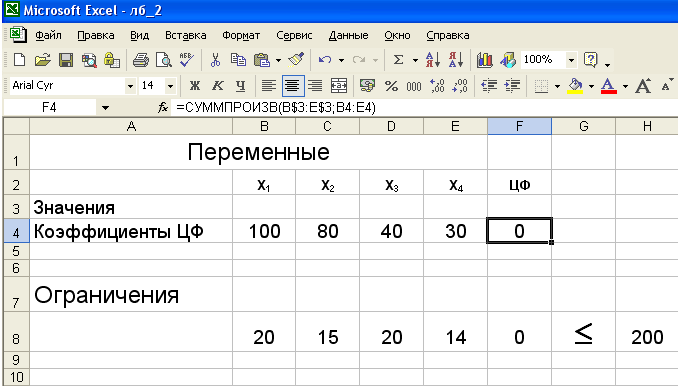
2.
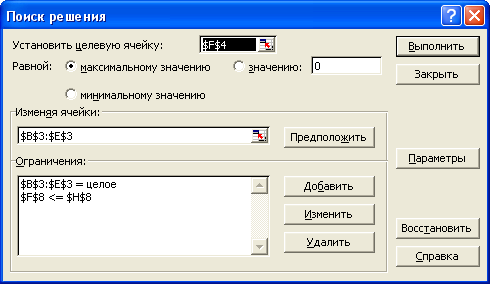
3.
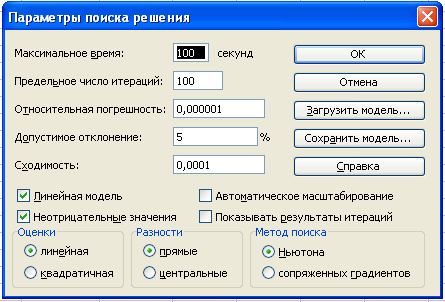
4.
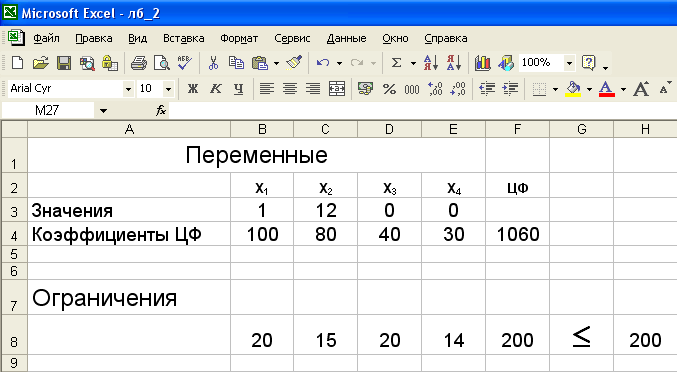
Таким образом, рекомендуемое управленческое решение с позиций принятого критерия оптимизации – следует погрузить 1 предмет первого типа и 12 предметов второго типа. В этом случае стоимость груза составит 1060 у. е., и грузоподъёмность будет использована полностью.
Раздел 6. Практические и лабораторные работы
ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
Задача. Планируется деятельность четырех промышленных предприятий (системы) на очередной год. Начальные средства: S0=5 условных единиц. Размеры вложения в каждое предприятие кратны 1 условной единице. Средства Х, выделенные k–му предприятию (k=1, 2, 3, 4), приносит в конце года прибыль fk(X). Функции fk(X) заданы таблично:
-
Х
f1(X)
f2(X)
f3(X)
f4(X)
1
2
3
4
5
8
10
11
12
18
6
9
11
13
15
3
4
7
11
18
4
6
8
13
16
Принято считать, что:
а) прибыль fk(X) не зависит от вложенных средств в другие предприятия;
б) прибыль от каждого предприятия выражается в одних условных единицах;
в) суммарная прибыль равна сумме прибылей, полученных от каждого предприятия.
Определить, какое количество средств нужно выделить каждому предприятию, чтобы суммарная прибыль наибольшей.
Решение.
Обозначим
через Xk
количество средств, выделенных k-му
предприятию. Суммарная прибыль равна
![]() .
Переменные X
удовлетворяют ограничениям:
.
Переменные X
удовлетворяют ограничениям:
![]() Требуется найти переменные X1,
X2,
X3,
X4,
удовлетворяющие данным ограничениям
и обращающие в максимум функцию Z.
Требуется найти переменные X1,
X2,
X3,
X4,
удовлетворяющие данным ограничениям
и обращающие в максимум функцию Z.
Рассмотрим особенности модели. Ограничения линейные, но переменные целочисленные, а функции fk(Xk) заданы таблично, поэтому нельзя применить методы целочисленного линейного программирования.
Схема решения задачи методом ДП имеет следующий вид: процесс решения распределения средств S0=5 можно рассматривать как 4-шаговый, номер шага совпадает с номером предприятия; выбор переменных X1, X2, X3, X4 – уравнения соответственно на I, II, III, IV шагах; Ŝ - конечное состояние процесса распределения – равно нулю, так как все средства должны быть вложены в производство, Ŝ=0. Покажем схему распределения:
У равнения
состояний в данной задаче имеют вид:
равнения
состояний в данной задаче имеют вид:
Sk=Sk-1-X,
(k=![]() ),
),
где Sk-параметр состояния – количество средств, оставшихся после k-го шага, т.е. средства, которые остается распределить между оставшимися 4-k предприятиями.
Введем в рассмотрение функцию Zk* (Sk-1) – условно оптимальную прибыль, полученную от k-го, (k+1)-го, ..., 4-го предприятий, если между ними распределялись оптимальным образом средства Sk-1 (0 Sk-1 5). уравнения на k-ом шаге удовлетворяют условию: 0 XkSk-1 (либо k-му предприятию ничего не выделяем, Xk=0, либо не больше того, что имеем к k-му шагу, Xk Sk-1 ).
Уравнения (1) и (4) имеют вид:
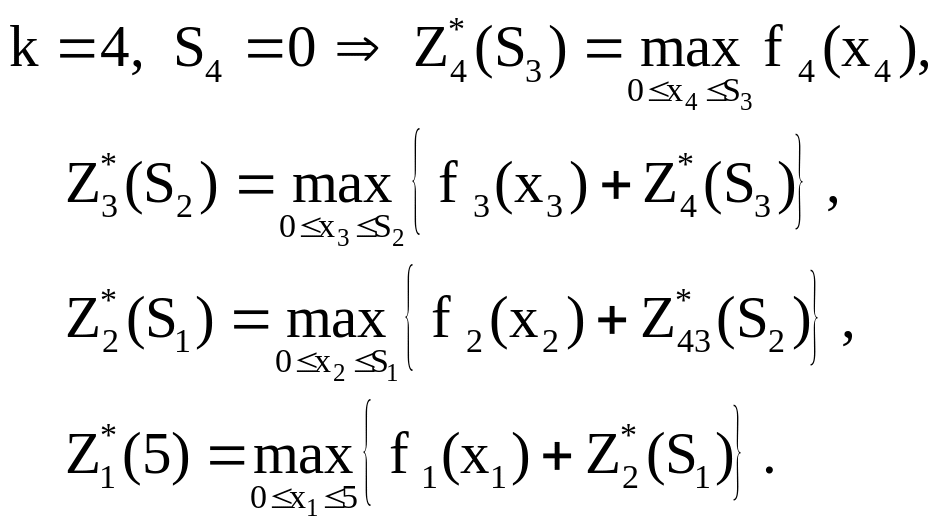
Последовательно решаем данные уравнения, проводя последовательную оптимизацию каждого шага.
IV шаг. Из таблицы условия видно, что f4(x) прибыли монотонно возрастают, поэтому все средства, оставшиеся к IV шагу, следует вложить в 4-е предприятие. При этом для возможных значений S3=0,1, ..., 5 получим: Z4*(S3)=f4(S3) и X4*(S3)=S3.
III шаг. Делаем все предположения относительно остатка средств S2 к III шагу: S2 может принимать значение 0, 1, 2, 3, 4, 5 (например, S2=0, если все средства отданы 1-му и 2-му предприятиям, S2=5, если 1-е и 2-е предприятие ничего не получили и т.д.). В зависимости от этого выбираем 0 X3S2 и сравниваем для разных X3, при фиксированном S2 значения суммы f3(X3)+Z4*(S3). Для каждого S2 наибольшее из этих значений есть Z3*(S2)- условная оптимальная прибыль, полученная при оптимальном распределении средств S2 между 3-м и 4-м предприятиями. Оптимизация дана в таблице при k=3. Для каждого значения S2 Z3*(S2) и Х3*(S2) помещены в графах 5 и 6 соответственно.
Sk-1 |
Xk |
Sk |
k=3 |
k=2 |
k=1 |
|||||||||||||||||
f3(X3)+ Z4*(S3) |
Z3* (S2) |
X3* (S2) |
f2(X2)+ Z3*(S2) |
Z2* (S1) |
X2* (S1) |
f1(X1)+ Z2*(S1) |
Z1* (S0) |
X1* (S0) |
||||||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|||||||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||||||
1 |
0 1 |
1 0 |
0+1=1 3+0=3 |
4 |
0 |
0+4=4 6+0=6 |
6 |
1 |
0+6=6 8+0=8 |
8 |
1 |
|||||||||||
2 |
0 1 2 |
2 1 0 |
0+6=6 3+4=7 4+0=4 |
7 |
1 |
0+7=7 6+4=10 9+0=9 |
10 |
1 |
0+10=10 8+6=14 10+0=10 |
14 |
1 |
|||||||||||
3 |
0 1 2 3 |
3 2 1 0 |
0+8=8 3+6=9 4+4=8 7+0=7 |
9 |
1 |
0+9=9 6+7=13 9+4=13 11+0=11 |
13 |
1 2 |
0+13=13 8+10=18 10+6=16 11+0=11 |
18 |
1 |
|||||||||||
4 |
0 1 2 3 4 |
4 3 2 1 0 |
0+13=13 3+8=11 4+6=10 7+4=11 11+0=11 |
13 |
0 |
0+13=13 6+9=15 9+7=16 11+4=15 13+0=13 |
16 |
2 |
0+16=16 8+13=21 10+10=20 11+6=17 12+0=12 |
21 |
1 |
|||||||||||
5 |
0 1 2 3 4 5 |
5 4 3 2 1 0 |
0+16=16 3+13=16 4+8=12 7+6=13 11+4=15 18+0=18 |
18
|
5 |
0+18=18 6+13=19 9+9=18 11+7=18 13+4=17 15+0+15 |
19 |
1 |
0+19=19 8+16=24 10+13=23 11+10=21 12+6=18 18+0=18 |
24 |
1
|
|||||||||||
 II
шаг. Условная оптимизация проведена в
таблице при k=2.
Для всех возможных значений S1
значения Z2*(S1)
и X2*(S1)
находятся в столбцах 8 и 9 соответственно;
первые слагаемые в столбце 7 – значения
f2(X2)
взяты из условия, а вторые слагаемые
взяты из столбца 5 при S2=S1–X2.
II
шаг. Условная оптимизация проведена в
таблице при k=2.
Для всех возможных значений S1
значения Z2*(S1)
и X2*(S1)
находятся в столбцах 8 и 9 соответственно;
первые слагаемые в столбце 7 – значения
f2(X2)
взяты из условия, а вторые слагаемые
взяты из столбца 5 при S2=S1–X2.
I шаг. Условная оптимизация проведена в таблице при k=1 для S0=5. Если X1=0, то S1=5, прибыль, полученная от четырех предприятий при условии, что S1=5 ед. средств между оставшимися тремя предприятиями будут распределены оптимально, равна f1(0)+ Z2*(5)=0+19=19. Если X1=1, то S2 =4. Суммарная прибыль при условии, что S2 =4 ед. средств между оставшимися тремя предприятиями будут распределены оптимально, равна f1(1)+Z2*(4)=8+16=24. Аналогично при X1=2, S2 =3 и f1(2)+ Z2*(3)=10+13=23; при X1=3, S2 =2 и f1(3)+ Z2*(2)=11+10=21; при X1=5, S2 =0 и f1(5)+ Z2*(0)=18+0=18. Сравнивая полученные значения, получим Z1*(5)=24 усл. ед. = Zmax при X1*= X1*(5)=1.
Вычисляя, получим S1* = 5 - 1 = 4, а по таблице в столбце 9 находим X2* = X2* (4) = 2. Далее находим S2* = 4-2 = 2, а в столбце 6 X3* = X3*(2) = 1. Наконец, S3* = 2-1 = 1 и X4* = X4*(1) = 1, т. е. X*(1; 2; 1; 1).
Максимум суммарной прибыли равен 24 усл. ед. средств при условии, что 1-му предприятию выделено 1 усл. ед.; 2-му предприятию – 2 усл. ед.; 3-му предприятию – 1 усл. ед.; 4-му предприятию – 1 усл. ед.
ТЕОРИЯ ИГР |
||||||||||||||||||||||||||||
Задача. В новом жилом микрорайоне создается ателье для ремонта в стационарных условиях |
||||||||||||||||||||||||||||
заявок на ремонт телеаппаратуры выражается (примерно) числами 2, 5, 8, 10 тысяч заявок |
|
|||||||||||||||||||||||||||
в год. Накопленный опыт работы аналогичных предприятий показывает, что прибыль от ремонта одного телевизора |
||||||||||||||||||||||||||||
в условиях ателье (ремонт на дому не учитывается) составляет |
||||||||||||||||||||||||||||
9 денежных единиц; потери, вызванные отказом в ремонте ввиду недостатка мощностей - 5 |
||||||||||||||||||||||||||||
денежных единиц; убытки от простоя специалистов и оборудования при отсутствии заявок |
||||||||||||||||||||||||||||
6 денежных единиц. |
||||||||||||||||||||||||||||
Составить матрицу эффективности работы создаваемого ателье при любом стечении об- |
||||||||||||||||||||||||||||
стоятельств. Дать рекомендации о мощности нового ателье. Решение. |
||||||||||||||||||||||||||||
Составим матрицу эффективности работы создаваемого ателье. |
||||||||||||||||||||||||||||
Обозначим множество стратегий X = {2,5,8,10} - мощности ателье, которые могут быть |
||||||||||||||||||||||||||||
выбраны для ремонота телевизоров в микрорайоне. Обозначим S = {0,2,5,8,10}- состояния |
||||||||||||||||||||||||||||
среды, возможная потребность в ремонте телеаппаратуры в микрорайоне. |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
Заполним ячейку таблицы, выделенную цветом. |
|||||||||||||||||||||
X S |
0 |
2 |
5 |
8 |
10 |
|
Мощность ателье 8 тыс. |
|||||||||||||||||||||
2 |
-12 |
18 |
3 |
-12 |
-22 |
|
телевизоров в год. Потребность - 5 |
|||||||||||||||||||||
5 |
-30 |
0 |
45 |
30 |
20 |
|
тыс. в год. Доход составит 9х5=45 тыс |
|||||||||||||||||||||
8 |
-48 |
-18 |
27 |
72 |
62 |
|
Убыток из-за простоя составит 6х3=18 |
|||||||||||||||||||||
10 |
-60 |
-30 |
15 |
60 |
90 |
|
тыс. Вписываем в эту клеточку 45 - 18= |
|||||||||||||||||||||
|
|
|
|
|
|
|
27 тыс. единиц в год. Возьмем сосед- |
|||||||||||||||||||||
нюю клеточку: мощность ателье 5 тыс. а потребность - 8 тыс. телевизоров в год. Доход соста- |
||||||||||||||||||||||||||||
вит 9х5=45 тыс. единиц. Потери, вызванные отказом в ремонте, составят 5х3=15 тыс. Вписы- |
||||||||||||||||||||||||||||
ваем в эту клеточку 45 - 15 = 30 тыс. единиц. Действуя аналогичным образом, заполним все |
||||||||||||||||||||||||||||
клеточки таблицы. |
||||||||||||||||||||||||||||
Приступаем к принятию решения в условиях неопределенности. |
||||||||||||||||||||||||||||
Критерий Вальда (критерий осторожного наблюдателя). |
||||||||||||||||||||||||||||
Этот критерий оптимизирует полезность в предположении, что среда находится в самом |
||||||||||||||||||||||||||||
невыгодном для наблюдателя состоянии. Обозначим lij значение, стоящее в клеточке на пере- |
||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Критерий в таком виде называется максиминным и используется в случае поиска наилучшей |
||||||||||||||||||||||||||||
стратегии в наихудших условиях, когда речь идет, как в данном случае, о выигрыше. Если выбирается |
||||||||||||||||||||||||||||
наилучшая стратегия в случае оценки потерь, то применяется минимаксный критерий |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
X S |
0 |
2 |
5 |
8 |
10 |
min |
|
|
|
|
|||||||||||||||||
opt |
2 |
-12 |
18 |
3 |
-12 |
-22 |
-22 |
|
|
|
|
|||||||||||||||||
|
5 |
-30 |
0 |
45 |
30 |
20 |
-30 |
|
|
|
|
|||||||||||||||||
|
8 |
-48 |
-18 |
27 |
72 |
62 |
-48 |
|
|
|
|
|||||||||||||||||
|
10 |
-60 |
-30 |
15 |
60 |
90 |
-60 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
-22 |
max |
|
|
|
|||||||||||||||||
Сначала определяем минимальное значение по каждой строке с помощью функции МИН. |
||||||||||||||||||||||||||||
Затем определяем максимальное значение из них с помощью функции МАКС. Таким образом, |
||||||||||||||||||||||||||||
по критерию Вальда следует строить телеателье с мощностью 2 тыс. телевизоров в год. |
||||||||||||||||||||||||||||
Критерий Лапласа |
||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
В данном случае число состояний среды равняется J=5 по числу столбцов изучаемой таблицы |
||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
X S |
0 |
2 |
5 |
8 |
10 |
|
|
|
|
|
|||||||||||||||||
|
2 |
-12 |
18 |
3 |
-12 |
-22 |
-5 |
|
|
|
|
|||||||||||||||||
|
5 |
-30 |
0 |
45 |
30 |
20 |
13 |
|
|
|
||||||||||||||||||
opt |
8 |
-48 |
-18 |
27 |
72 |
62 |
19 |
|
|
|
||||||||||||||||||
|
10 |
-60 |
-30 |
15 |
60 |
90 |
15 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
max |
19 |
|
|
|
|
|||||||||||||||||
По критерию Лапласа следует строить телеателье с мощностью 8 тыс. ремонтов телевизоров в год. |
||||||||||||||||||||||||||||
Критерий Гурвица |
||||||||||||||||||||||||||||
Критерий основан на следующих предположениях: среда может находится в самом невы- |
||||||||||||||||||||||||||||
годном состоянии с вероятностью 1 - α и в самом выгодном с вероятностью α, где α - коэффи- |
||||||||||||||||||||||||||||
циент доверия. Тогда решающее правило записывается так:
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
Если α = 1, то приходим к решающему правилу вида |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
X S |
0 |
2 |
5 |
8 |
10 |
|
|
||||||||||||||||||||
|
2 |
-12 |
18 |
3 |
-12 |
-22 |
|
|
||||||||||||||||||||
|
5 |
-30 |
0 |
45 |
30 |
20 |
|
|
|
|
|
|||||||||||||||||
|
8 |
-48 |
-18 |
27 |
72 |
62 |
|
|
|
|
|
|||||||||||||||||
|
10 |
-60 |
-30 |
15 |
60 |
90 |
|
|
|
|
|
|||||||||||||||||
|
X α |
0,1 |
0,2 |
0,5 |
0,9 |
max |
min |
|
|
|
|
|||||||||||||||||
|
2 |
-18 |
-14 |
-2 |
14 |
18 |
-22 |
|
|
|
|
|||||||||||||||||
|
5 |
-22,5 |
-15 |
7,5 |
37,5 |
45 |
-30 |
|
|
|
|
|||||||||||||||||
|
8 |
-36 |
-24 |
12 |
60 |
72 |
-48 |
|
|
|
|
|||||||||||||||||
|
10 |
-45 |
-30 |
15 |
75 |
90 |
-60 |
|
|
|
|
|||||||||||||||||
|
max |
-18 |
-14 |
15 |
75 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Оптимальная мощность телеателье в зависимости от α представлена в таблице |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
α |
0,1 |
0,2 |
0,5 |
0,9 |
|
|
|
|
|
|
|||||||||||||||||
|
Xopt |
2 |
2 |
10 |
10 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Критерий Сэвиджа (минимизации "сожалений"). |
||||||||||||||||||||||||||||
"Сожаление" или риск есть разность между наилучшим значением в столбце j и всеми осталь- |
||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
Вычитаем это значение из всех остальных в этом столбце:
|
|
|
|
|||||||||||||||||||||||||
Строим матрицу "сожалений". |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
X S |
0 |
2 |
5 |
8 |
10 |
|
|
||||||||||||||||||||
|
2 |
-12 |
18 |
3 |
-12 |
-22 |
|
|
||||||||||||||||||||
|
5 |
-30 |
0 |
45 |
30 |
20 |
|
|
||||||||||||||||||||
|
8 |
-48 |
-18 |
27 |
72 |
62 |
|
|
||||||||||||||||||||
|
10 |
-60 |
-30 |
15 |
60 |
90 |
|
|
||||||||||||||||||||
|
max |
-12 |
18 |
45 |
72 |
90 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
X S |
0 |
2 |
5 |
8 |
10 |
min |
|
|
|||||||||||||||||||
|
2 |
0 |
0 |
-42 |
-84 |
-112 |
-112 |
|
|
|||||||||||||||||||
|
5 |
-18 |
-18 |
0 |
-42 |
-70 |
-70 |
|
|
|||||||||||||||||||
Xopt |
8 |
-36 |
-36 |
-18 |
0 |
-28 |
-36 |
|
|
|||||||||||||||||||
|
10 |
-48 |
-48 |
-30 |
-12 |
0 |
-48 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
max |
-36 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
В случае, если речь идет о потерях, то используется минимаксный критерий. |
||||||||||||||||||||||||||||
Подведем итог нашего исследования: |
||||||||||||||||||||||||||||
Инвестиции вкладываются по критерию Вальда в сторительство телеателье на 2 тыс.ремон- |
||||||||||||||||||||||||||||
тов в год. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
По критерию Лапласа следует строить телеателье на 8 тыс. ремонтов телевизоров в год. |
||||||||||||||||||||||||||||
По критерию Гурвица следует строить телеателье на 2 тыс. ремонтов телевизоров в год, если. |
||||||||||||||||||||||||||||
обстановка не внушает доверия, и 10 тыс. - если обстановка благоприятная. |
||||||||||||||||||||||||||||
По критерию Сэвиджа следует строить телеателье на 8 тыс. ремонтов телевизоров в год. |
||||||||||||||||||||||||||||
Резюме. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Если даже минимальный риск недопустим, следует применять критерий Вальда. |
||||||||||||||||||||||||||||
Если наоборот, определенный риск вполне приемлем и заказчик намерен вложить в предпри- |
||||||||||||||||||||||||||||
ятие столько средств, чтобы потом не сожалеть, что вложено слишком мало, то выбирают |
||||||||||||||||||||||||||||
СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ
Задача. В вычислительный центр коллективного пользования с тремя ЭВМ поступают заказы от предприятий на вычислительные работы. Если работают все три ЭВМ, то вновь поступающий заказ не принимается, и предприятие вынуждено обратиться в другой вычислительный центр. Среднее время работы с одним заказом составляет 3 ч. Интенсивность потока заявок 0,25 (1/ч). Найти предельные вероятности состояний и показатели эффективности работы вычислительного центра.
Решение. По условию n=3, λ=0,25(1/ч), об.=3 (ч). Интенсивность потока обслуживаний μ=1/ об.=1/3=0,33. Интенсивность нагрузки ЭВМ по формуле (24) ρ=0,25/0,33=0,75. Найдем предельные вероятности состояний:
по формуле (25) p0=(1+0,75+0,752/2!+0,753/3!)-1=0,476;
по формуле (26) p1=0,75∙0,476=0,357; p2=(0,752/2!)∙0,476=0,134; p3=(0,753/3!)∙0,476=0,033 т.е. в стационарном режиме работы вычислительного центра в среднем 47,6% времени нет ни одной заявки, 35,7% — имеется одна заявка (занята одна ЭВМ), 13,4% — две заявки (две ЭВМ), 3,3% времени — три заявки (заняты три ЭВМ).
Вероятность отказа (когда заняты все три ЭВМ), таким образом, Pотк.=p3=0,033.
По формуле (28) относительная пропускная способность центра Q = 1-0,033 = 0,967, т.е. в среднем из каждых 100 заявок вычислительный центр обслуживает 96,7 заявок.
По формуле (29) абсолютная пропускная способность центра A= 0,25∙0,967 = 0,242, т.е. в один час в среднем обслуживается 0,242 заявки.
По формуле (30) среднее число занятых ЭВМ =0,242/0,33 = 0,725, т.е. каждая из трех ЭВМ будет занята обслуживанием заявок в среднем лишь на 72,5/3 =24,2%.
При оценке эффективности работы вычислительного центра необходимо сопоставить доходы от выполнения заявок с потерями от простоя дорогостоящих ЭВМ (с одной стороны, у нас высокая пропускная способность СМО, а с другой стороны — значительный простой каналов обслуживания) и выбрать компромиссное решение.
Задача. В порту имеется один причал для разгрузки судов. Интенсивность потока судов равна 0,4 (судов в сутки). Среднее время разгрузки одного судна составляет 2 суток. Предполагается, что очередь может быть неограниченной длины. Найти показатели эффективности работы причала, а также вероятность того, что ожидают разгрузки не более чем 2 судна.
Решение. Имеем ρ = λ/μ = μ об.=0,4∙2=0,8. Так как ρ = 0,8 < 1, то очередь на разгрузку не может бесконечно возрастать и предельные вероятности существуют. Найдем их.
Вероятность того, что причал свободен, по (33) p0 = 1 - 0,8 = 0,2, а вероятность того, что он занят, Pзан. = 1—0,2 = 0,8. По формуле (34) вероятности того, что у причала находятся 1, 2, 3 судна (т.е. ожидают разгрузки 0, 1, 2 судна), равны p1 = 0,8(1-0,8) = 0,16; p2 = 0,82∙(1-0,8) = 0,128; p3 = 0,83∙(1-0,8) = 0,1024.
Вероятность того, что ожидают разгрузку не более чем 2 судна, равна
![]()
По формуле (40) среднее число судов, ожидающих разгрузки
![]()
а среднее время ожидания разгрузки по формуле (15.42)
![]() (сутки).
(сутки).
По формуле (36) среднее число судов, находящихся у причала, Lсист. = 0,8/(1-0,8) = 4 (сутки) (или проще по (37) Lсист. = 3,2+0,8 = 4 (сутки), а среднее время пребывания судна у причала по формуле (41) Tсист = 4/0,8 = 5 (сутки).
Очевидно, что эффективность разгрузки судов невысокая. Для ее повышения необходимо уменьшение среднего времени разгрузки судна об. либо увеличение числа причалов п.
Задача
. В универсаме к
узлу расчета поступает поток покупателей
с интенсивностью
= 81 чел. в час. Средняя продолжительность
обслуживания контролером-кассиром
одного покупателя
![]() = 2 мин.
Определить:
= 2 мин.
Определить:
а. Минимальное количество контролеров-кассиров пmin, при котором очередь не будет расти до бесконечности, и соответствующие характеристики обслуживания при n=nmin.
б.
Оптимальное количество nопт.
контролеров-кассиров, при котором
относительная величина затрат Сотн.,
связанная с издержками на содержание
каналов обслуживания и с пребыванием
в очереди покупателей, задаваемая,
например, как
![]() ,
будет минимальна, и сравнить характеристики
обслуживания при n=nmin
и n=nопт.
,
будет минимальна, и сравнить характеристики
обслуживания при n=nmin
и n=nопт.
в. Вероятность того, что в очереди будет не более трех покупателей.
Решение.
а. По условию = 81(1/ч) = 81/60 = 1,35 (1/мин.). По формуле (24) = / = = 1,352 = 2,7. Очередь не будет возрастать до бесконечности при условии /n < 1, т.е. при n > = 2,7. Таким образом, минимальное количество контролеров-кассиров nmin = 3.
Найдем характеристики обслуживания СМО при п = 3.
Вероятность того, что в узле расчета отсутствуют покупатели, по формуле (45) p0 = =(1+2,7+2,72/2!+2,73/3!+2,74/3!(3-2,7))-1 = 0,025, т.е. в среднем 2,5 времени контролеры-кассиры будут простаивать.
Вероятность того, что в узле расчета будет очередь, по (48) Pоч.= (2,74/3!(3-2,7))0,025 = 0,735
Среднее число покупателей, находящихся в очереди, по (50) Lоч. = (2,74/3∙3!( 1-2,7/3)2)0,025 = 7,35.
Среднее время ожидания в очереди по (42) Tоч.= 7,35/1,35 = 5,44 (мин).
Среднее число покупателей в узле расчета по (51) Lсист.= 7,35+2,7 = 10,05.
Среднее время нахождения покупателей в узле расчета по (41) Tсист. = 10,05/1,35 = 7,44 (мин).
Характеристика обслуживания |
Число контролеров-кассиров |
||||
3
|
4
|
5
|
6
|
7
|
|
Вероятность простоя контролеров-кассиров p0
|
0,025
|
0,057
|
0,065
|
0,067
|
0,067
|
Среднее число покупателей в очереди Tоч.
|
5,44
|
0,60
|
0,15
|
0,03
|
0,01
|
Относительная величина затрат Сотн.
|
18,54
|
4,77
|
4,14
|
4,53
|
5,22
|
Среднее число контролеров-кассиров, занятых обслуживанием
Таблица 1
покупателей, по (49) = 2,7.
Коэффициент (доля) занятых обслуживанием контролеров-кассиров
= ρ/n = 2,7/3 = 0,9.
Абсолютная пропускная способность узла расчета А = 1,35 (1/мин), или 81 (1/ч), т.е. 81 покупатель в час.
Анализ характеристик обслуживания свидетельствует о значительной перегрузке узла расчета при наличии трех контролеров-кассиров.
б. Относительная величина затрат при n = 3
Cотн.
=
![]() =
3/1,35+3∙5,44 = 18,54.
=
3/1,35+3∙5,44 = 18,54.
Рассчитаем относительную величину затрат при других значениях п (табл. 1).
Как видно из табл. 2, минимальные затраты получены при n = nопт. = 5 контролерах-кассирах.
Определим характеристики обслуживания узла расчета при n = nопт. = 5 . Получим Pоч. = 0,091; Lоч. = 0,198; Точ. = 0,146 (мин); Lсист. = 2,90; Tснст. = 2,15 (мин); = 2,7; k3 = 0,54.
Как видим, при n = 5 по сравнению с n = 3 существенно уменьшились вероятность возникновения очереди Pоч., длина очереди Lоч. и среднее время пребывания в очереди Tоч. и соответственно среднее число покупателей Lсист. и среднее время нахождения в узле расчета Tсист., а также доля занятых обслуживанием контролеров k3. Но среднее число занятых обслуживанием контролеров-кассиров и абсолютная пропускная способность узла расчета А естественно не изменились.
в. Вероятность того, что в очереди будет не более 3 покупателей, определится как
-
P(r ≤ 3) = p1+ p2+ p3+ p4+ p5+
p5+1+ p5+2+ p5+3 =
(когда заняты от 1 до 5
контролеров-кассиров)
(когда в очереди стоят
от 1 до 3 покупателей)
= 1- Pоч.+ p5+1+ p5+2+ p5+3, где каждое слагаемое найдем по формулам (45) – (48). Получим при n=5:
![]()
(Заметим, что в случае n=3 контролеров-кассиров та же вероятность существенно меньше: P(r ≤ 3) =0,464).
СЕТЕВОЕ ПЛАНИРОВАНИЕ И УПРАВЛЕНИЕ
З адача.
Найти кратчайший маршрут, ведущий от А
к В
на графе, изображенном на рис.28.
адача.
Найти кратчайший маршрут, ведущий от А
к В
на графе, изображенном на рис.28.
Решение. Оформляем решение в виде таблицы.
Делаем вывод, что кратчайшим является маршрут А А2 А1 А4 А3 В, и его вес равен 14.
З адача.
Построить сетевой график работы по
данным, приведенным на рис.2.
адача.
Построить сетевой график работы по
данным, приведенным на рис.2.

Решение. Заполняем сначала левые сектора. Результат приведен на рис.3.
З атем
заполняем правые сектора. Определяем
цепь, задающую жесткий график работ.
Окончательный результат приведен на
рис.4.
атем
заполняем правые сектора. Определяем
цепь, задающую жесткий график работ.
Окончательный результат приведен на
рис.4.

Задача.Построить максимальный поток по транспортной сети, изображенной на рис. 5.
Решение. На транспортной сети задан нулевой поток. Выполняем пункты 1.2 – 1.4. Возьмем сначала следующий путь от начала к концу: x0 x1 x2 z (этот неестественный на первый взгляд путь лучше проиллюстрирует работу алгоритма). Поток по этому пути можно увеличить на 1, в результате все ребра станут насыщенными, и мы их условно разрываем.
Следующий возможный путь x0 x2 x1 z. Поток по этому пути также можно увеличить на 1, в результате станет насыщенным ребро x2 x1, которое мы условно разрываем.
Больше путей от начала к концу сети не существует. Мы получили насыщенную сеть, изображенную на рис. 6 а).
П ереходим
к пометке вершин. Сначала помечаем –0
вершину x0.
Вершину x1
пока
пометить не можем, так как от x0
к ней идет насыщенное ребро. Но от x0
к x2
идет
ненасыщенное ребро, поэтому x2
помечаем
+0. Вершину z
пока пометить не можем, но зато помечаем
x1,
так как от x1
к x2
идет
непустое ребро. Поэтому x1
помечаем
–2. Теперь вершину z
можно пометить +1, так как от x1
к z
идет
ненасыщенное ребро. Соответствующие
пометки показаны на рис. 6 б).
ереходим
к пометке вершин. Сначала помечаем –0
вершину x0.
Вершину x1
пока
пометить не можем, так как от x0
к ней идет насыщенное ребро. Но от x0
к x2
идет
ненасыщенное ребро, поэтому x2
помечаем
+0. Вершину z
пока пометить не можем, но зато помечаем
x1,
так как от x1
к x2
идет
непустое ребро. Поэтому x1
помечаем
–2. Теперь вершину z
можно пометить +1, так как от x1
к z
идет
ненасыщенное ребро. Соответствующие
пометки показаны на рис. 6 б).
Так
как вершина
z
оказалась помеченной, то выполняем
следующее. Движение от х0
к z,
определяемое пометкой вершин (начиная
от z
и двигаясь в обратную сторону),
соответствует цепочке
![]() .
В этой цепочке поток по ребрам,
ориентированным в направлении движения,
можно увеличивать, а против движения –
уменьшать на одно и то же число. Заключаем,
что это число 1, после перераспределения
потока ребро x2
x1
станет пустым. Новый поток изображен
на рис. 6в).
.
В этой цепочке поток по ребрам,
ориентированным в направлении движения,
можно увеличивать, а против движения –
уменьшать на одно и то же число. Заключаем,
что это число 1, после перераспределения
потока ребро x2
x1
станет пустым. Новый поток изображен
на рис. 6в).
Снова
переходим к пометке вершин. Опять
помечаем –0 вершину x0
и +0 вершину x2.
Но ни x1,
ни z
пометить нельзя, так как к ним от
помеченных вершин ведут насыщенные
ребра, а от x1
к x2
пустое. Значит, работа алгоритма
завершена. а.
Поток на рис. 6 в) является максимальным.
а.
Поток на рис. 6 в) является максимальным.
Задача.Построить минимальное остовное дерево для графа, изображенного на рис.7.
Решение. Действуя по жадному алгоритму, получим минимальное остовное дерево, изображенное на рис.8. Оно выделено жирными линиями. Штриховыми линиями выделены ребра, которые в процессе решения исключались из рассмотрения, так как образовывали циклы с ранее включенными в дерево ребрами. Вес построенного минимального остовного дерева равен 24.


При выполнении лабораторных работ целесообразно использовать средства Microsoft Ехсеl. Для этого необходима надстройка Поиск решения, которая позволяет реализовывать модели линейной, нелинейной и дискретной оптимизации.
Если в меню Сервис отсутствует команда Поиск решения необходимо выполнить следующие действия:
– выбрать команду Сервис Надстройки;
– в диалоговом окне Надстройки установить флажок Поиск решения;
– щелкнуть ОК.
После этого в меню Сервис появится новая команда Поиск решения.
Рассмотрим решение некоторых задач.
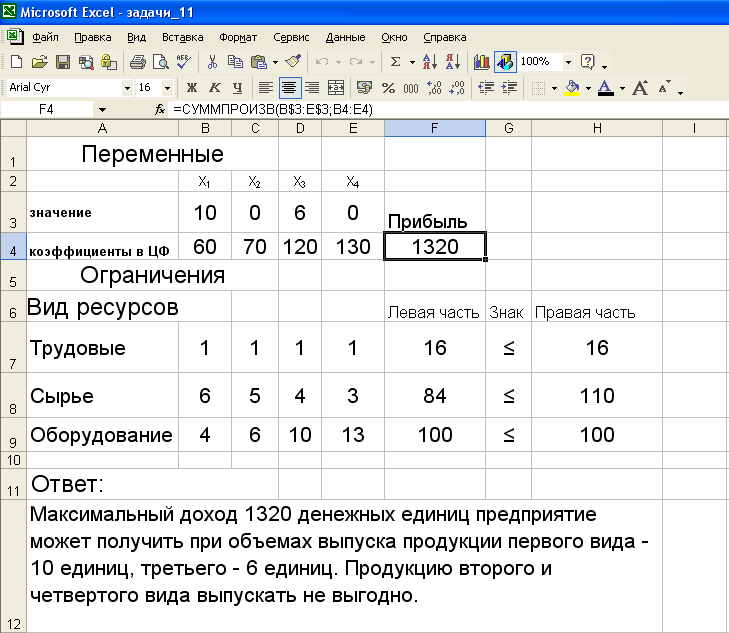
Задача1. Предприятие выпускает продукцию четырех видов П1, П2, П3, П4 с использованием для этого ресурсов, виды и нормы расхода по которым, а также уровень получаемой от их реализации прибыли приведены в таблице. Составьте оптимальный план производства продукции, дающий максимальную прибыль.
Вид ресурса |
Вид продукции |
Запас ресурса |
|||
П1 |
П2 |
П3 |
П4 |
||
Трудовые |
1 |
1 |
1 |
1 |
16 |
Сырье |
6 |
5 |
4 |
3 |
110 |
Оборудование |
4 |
6 |
10 |
13 |
100 |
Прибыль |
60 |
70 |
120 |
130 |
|
Экономико-математическая модель:
Введём необходимые обозначения: пусть xj (j=1,2,3,4) – объемы каждого вида продукции. Тогда ЭММ задачи запишется следующим образом:
max f(x1, x2, x3, x4) =60x1+70x2+120x3+130x4,

Решение.
1. Создадим форму для ввода условий задачи. Для этого запустим Excel, выбрав Microsoft Excel из подменю Программы главного меню Windows. Создадим текстовую форму – таблицу для ввода условий задачи.
2. Укажем адреса ячеек, в которые будет помещен результат решения (изменяемые ячейки). Значения компонент вектора X=(x1, x2, x3, x4) поместим в ячейках ВЗ:ЕЗ, оптимальное значение целевой функции – в ячейку F4.
3. Введем исходные данные задачи в созданную форму-таблицу:
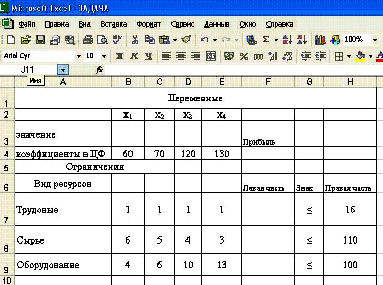
4.Введем зависимость для целевой функции:
установить курсор в ячейку F4.
кликнуть по кнопке Мастер функций, расположенной на панели инструментов.
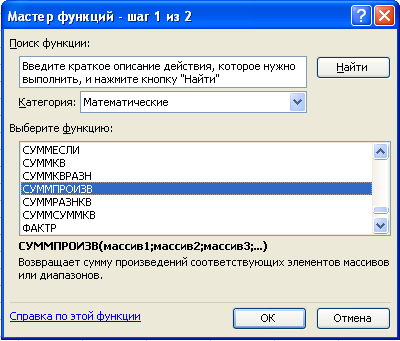
на экране появляется диалоговое окно Мастер функций – шаг 1 из 2.
выбрать категорию Математические;
выбрать функцию СУММПРОИЗВ
на экране появляется диалоговое окно СУММПРОИЗВ;
в строку Массив 1 введем В$3:Е$3;
в строку Массив 2 введем В4:Е4;
кликнуть по кнопке ОК. На экране в ячейку F4 введена функция.
5. Ввести зависимости для ограничений:
курсор в ячейку F4; кнопка Копировать;
курсор в ячейку F7; кнопка Вставить;
курсор в ячейку F8; кнопка Вставить;
курсор в ячейку F9; кнопка Вставить.
В строке Меню установить указатель мыши на имя Сервис. В развернутом меню выбрать команду Поиск решения.
6. Назначим целевую функцию (установим целевую ячейку):
курсор в строку Установить целевую ячейку;
введем адрес ячейки $F$4;
введем направление целевой функции в зависимости от условия задачи – Максимальному значению;
курсор в строку Изменяя ячейки;
введем адреса искомых переменных В$3:E$3.
7. Введем ограничения:
кнопка Добавить. Появляется диалоговое окно Добавление ограничения;
в строке Ссылка на ячейку введем адрес $F$7: $F$9 (или укажем на листе, т.е. щелкнуть на маленькой красной стрелке рядом с этим полем, выйти в таблицу, выделить ячейки F7:F9, нажать клавишу F4, при этом ссылка станет абсолютной $F$7: $F$9, щелкнуть на красной стрелке и вернуться в блок Поиска решения, при этом нужный адрес будет введен);
выберем знак ограничения <=;
в строке Ограничения введем адрес $Н$7: $Н$9;
после введения ограничения кнопка ОК.

8. Введем параметры для решения ЗЛП:
в диалоговом окне Поиск решения кнопка Параметры.
на экране диалоговое окно Параметры поиска решения
установим флажки:
Линейная модель (это обеспечит применение симплекс-метода)
Неотрицательные значения;
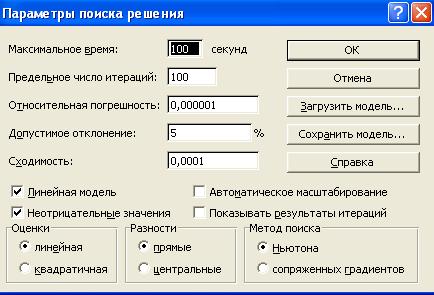
кнопка ОК. На экране диалоговое окно Поиск решения;
кнопку Выполнить.
в диалоговом окно Результаты поиска решения
выбрать Сохранить найденное решение
кнопка OK
На экране представлена исходная таблица с заполненными ячейками ВЗ:ЕЗ для значений X и ячейка F4 с максимальным значением целевой функции. Введем экономическую интерпретацию полученных результатов: «Максимальный доход 1320 денежных единиц предприятие может получить при объемах выпуска продукции первого вида – 10 единиц, третьего вида – 6 единиц. Продукцию второго и четвертого вида выпускать не выгодно.»
Задача 2. Перед менеджером нефтяной компании «Магнум» стоит задача создания схемы поставки нефтепродуктов от четырех нефтеперерабатывающих комплексов компании к пяти регионам страны. Одним из основных условий поставленной задачи является минимизация стоимости перевозок, при этом все мощности нефтеперерабатывающих комплексов должны бьть реализованы и все потребности регионов должны быть удовлетворены.
Мощности поставщиков и мощности потребителей, а также стоимость перевозок нефтепродуктов представлены в следующей таблице (в условных единицах).
Мощности поставщиков |
Мощности потребителей |
||||
600 |
400 |
700 |
500 |
1000 |
|
700 |
4 |
8 |
5 |
1 |
6 |
800 |
3 |
5 |
2 |
3 |
4 |
900 |
2 |
6 |
5 |
4 |
3 |
800 |
1 |
4 |
3 |
5 |
3 |
Решение.
В данном случае мощности поставщиков нефтепродуктов и потребности регионов в них совпадают, т.е. имеем дело с закрытой моделью транспортной задачи.
Ввод условий задачи состоит из следующих основных этапов.
1. Создание формы для решения задачи.
2. Ввод граничных условий.
3. Ввод исходных данных.
4. Назначение целевой функции.
5. Ввод зависимостей из математической модели.
6. Ввод ограничений.
7. Просмотр результатов и печать отчета.
Рассмотрим более подробно каждый из этих этапов.
1. Создание формы для решения задачи предполагает создание матрицы перевозок. Для этого необходимо выполнить резервирование изменяемых ячеек: в блок ячеек ВЗ:F6 заполняется значением 1. Таким образом, резервируется место, где после решения задачи будет находиться распределение поставок, обеспечивающее минимальные затраты на перевозку груза (нефтепродуктов).
2. Ввод граничных условий.
Введение условия реализации мощностей поставщиков, т.е.
![]()
где ai – мощность i-го поставщика;
xi, j – объем поставки груза от i-го поставщика к j-му потребителю;
п – количество потребителей.
Для этого необходимо выполнить следующие операции:
курсор в ячейку АЗ;
кнопка Автосумма;
выделить необходимые для суммирования ячейки ВЗ:FЗ;
нажать ENTER – подтверждение ввода формулы для суммирования.
Аналогичные действия выполнить для ячеек А4, А5, А6, т.е. ввести условия реализации мощностей всех поставщиков (для всех строк). Эти действия можно реализовать иначе:
курсор в АЗ;
кнопка Копировать;
выделить ячейки А4:А6;
кнопка Вставить.
Введение условия удовлетворения запросов потребителей, т.е.
![]()
где bj – мощность j-го потребителя;
т – количество поставщиков.
Для этого необходимо выполнить следующие операции:
курсор в В7;
кнопка Автосумма. При этом автоматически выделятся весь столбец ВЗ:В6;
ЕNTER – подтверждение суммирования показателей выделенного столбца.
Последовательность этих действий выполнить для ячеек С7:F7, или же:
курсор в В7;
кнопка Копировать;
выделить С7:F7;
кнопка Вставить.
Таким образом, введены ограничения для всех поставщиков и всех потребителей.
3. Ввод исходных данных.
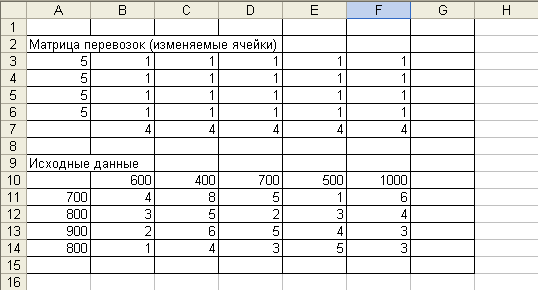
В конкретном примере осуществляется ввод мощностей четырех нефтеперерабатывающих предприятий (ячейки А11:А14), потребности регионов в их продукции (В10:F10), а также удельные затраты по доставке нефтепродуктов от конкретного поставщика потребителю (блок В11:F14).
4. Назначение целевой функции.
Для вычисления значения целевой функции, соответствующей минимальным суммарным затратам на доставку груза, необходимо в определенную ячейку ввести формулу для ее вычисления:
![]()
где cij – стоимость доставки единицы груза от i-го поставщика к j-му потребителю;
хij - объем поставки груза от i-го поставщика к j-му потребителю.
Для этого:
курсор в ячейку В15. В данную ячейку будет помещаться значение целевой функции после решения задачи;
кнопка Мастер функций;
На экране появится диалоговое окно Мастер функции шаг - 1 из 2
выбрать категорию Математические;
выбрать функцию СУММПРОИЗВ;
В задаче целевая функция представляет собой произведение удельных затрат на доставку груза (расположенных в блоке ячеек В11:F14) и объемов поставок для каждого потребителя (содержимое ячеек ВЗ:F6). Для этого:
в строку Массив 1 ввести В11:F14;
в строку Массив 2 ввести ВЗ:F6;
кнопка ОК.
В поле ячейки В15 появится некоторое числовое значение, равное произведению единичных поставок на удельные коэффициенты затрат по доставке грузов (число 77 в данной задаче).
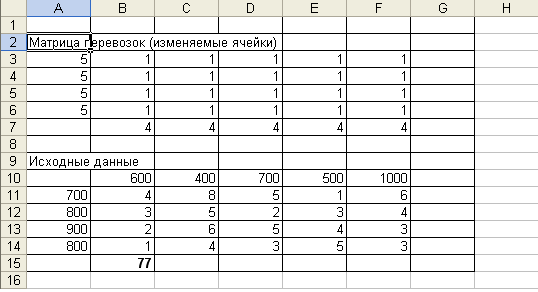
5. Ввод зависимостей из математической модели:
выбрать Сервис Поиск решения;
курсор в Установить целевую ячейку;
ввести (выбрать) адрес $В$15.
Таким образом, производится указание ячейки, куда при решении задачи помещается значение целевой функции.
Или:
поставить курсор в В15
выбрать Сервис Поиск решения.
При этом осуществится автоматический ввод адреса $В$15 в поле адреса целевой ячейки;
установить направление изменения целевой функции: минимальному значению.
Ввести адреса изменяемых ячеек ВЗ:F6. Для этого:
щелкнуть в поле Изменяя ячейки;
ввести адреса $В$3:$F$6 (или укажем на листе).
Ввести ограничение задачи. В матрицу перевозок, содержащую исходные данные по задаче, необходимо ввести условие реализации мощностей всех поставщиков. Для этого:
кнопка Добавить. Появляется диалоговое окно Добавление ограничения;
в строке Ссылка на ячейку введем адреса (или укажем на листе) $А$3:$А$6;
выберем знак ограничения =;
в строке Ограничение введем адреса (или укажем на листе) $А$11:$А$14;
кнопка OK
На экране появится диалоговое окно Поиск решения с введённым условием.
Далее вводится ограничение, которое реализует условие удовлетворения мощностей всех потребителей. Для этого:
кнопка Добавить. Появляется диалоговое окно Добавление ограничения;
в строке Ссылка на ячейку введем адреса (или укажем на листе) $В$7:$F$7;
выберем знак ограничения =;
в строке Ограничение введем адреса (или укажем на листе) $В$10:$F$10;
кнопка OK
6. Ввод ограничений.
Далее необходимо установить ограничения на решение задачи. Для этого:
кнопка Параметры.
на экране диалоговое окно Параметры поиска решения:
установим флажки:
Линейная модель (это обеспечит применение симплекс-метода)
Неотрицательные значения, так как объемы поставок груза отрицательной величиной быть не могут;;
кнопка ОК.
на экране появится диалоговое окно Поиск решения;
кнопка Выполнить.
7. Просмотр результатов и печать отчета. После выполнения всех вышеуказанных действий на экран выводится окно Результаты поиска решения
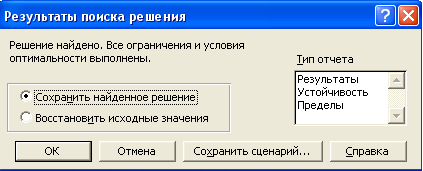
В окне Тип отчета выбрать интересующий вид отчета.
кнопка ОК.
Внизу страницы экрана содержится сообщение Отчет по результатам 1. Щелкнуть на этом сообщении, на экран выводятся результаты решения задачи, которые можно распечатать.
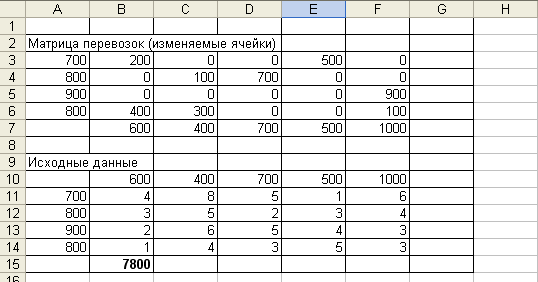
При нажатии Лист 1 происходит возврат в программу к исходным данным.
В матрице перевозок содержатся оптимальные объемы поставок грузов от поставщика потребителям, дающие минимум затрат на доставку. Значение целевой функции содержится в ячейке В15 и для конкретной задачи равно 7800. Из вышеизложенного можно сделать следующий вывод: минимум затрат на доставку нефтепродуктов, равный 7800 условных денежных единиц, будет обеспечен при следующем плане поставок:
от первого поставщика первому потребителю в объеме 2 (единиц и четвертому в объеме 500 единиц (условных);
от второго поставщика второму потребителю в объеме 18 единиц и третьему потребителю в объеме 700 единиц (условных);
от третьего поставщика пятому потребителю в объеме 900 единиц (условных);
от четвертого поставщика первому потребителю в объеме 400 единиц и второму потребителю в объеме 300 единиц (условных).
При данной схеме поставок мощности всех поставщиков будут реализованы и спросы всех потребителей будут удовлетворены.
Замечание. Задача о назначении сводится к транспортной при граничных условиях (вместо мощностей поставщиков и потребителей).
Введение условия назначения работника только на одну должность, т.е.
![]() ,
где хij–
назначение i-го
работника на j-ую
должность; т – количество
вакантных должностей
,
где хij–
назначение i-го
работника на j-ую
должность; т – количество
вакантных должностей
Введение условия заполнения вакантной должности, т.е.
![]()
Задача 3. Необходимо сформировать оптимальный портфель Марковица (минимального риска) трех ценных бумаг с эффективностями и рисками: (4,10), (10,40), (40,80). Нижняя граница доходности портфеля задана равной 15.
Экономико-математическая модель
Пусть xj, j= 1,2,3 – доля капитала, потраченная на покупку ценных бумагу j-го вида (весь выделенный капитал принимается за 1)
![]()

Решение. Приведенная ЭММ является моделью задачи нелинейного программирования. Специальный (рабочий) лист может быть подготовлен в виде:
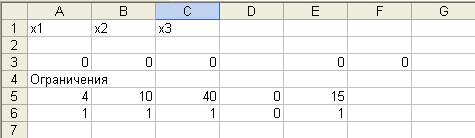
формулы этого листа приведены в ячейках.

Диалоговое окно Поиск решения с введенными ограничениями, соответствующее приведенному выше рабочему листу:

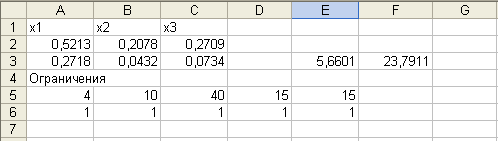
Реализуя приведенную модель средствами MS Excel, будем иметь оптимальный портфель Марковица:
х1 = 0,5213, х2 = 0,2078, х3 = 0,2709,
т.е. доли ценных бумаг оказались равными 52,13%; 20,78% и 27,09%. При этом минимальный риск – 23,79, доходность портфеля оказалась равной заданной – 15.
Задача 4. Планируется деятельность четырех промышленных предприятий (системы) на очередной год. Начальные средства: S0=5 условных единиц. Размеры вложения в каждое предприятие кратны 1 условной единице. Средства Х, выделенные k–му предприятию (k=1, 2, 3, 4), приносит в конце года прибыль fk(X). Функции fk(X) заданы таблично:
-
Х
f1(X)
f2(X)
f3(X)
f4(X)
1
2
3
4
5
8
10
11
12
18
6
9
11
13
15
3
4
7
11
18
4
6
8
13
16
Определить, какое количество средств нужно выделить каждому предприятию, чтобы суммарная прибыль наибольшей.
Решение.
Создадим текстовую форму – таблицу для ввода условий задачи. Введем исходные данные задачи в созданную форму-таблицу:

В ячейку E15 введем формулу
=ИНДЕКС($B$3:$F$8; ПОИСКПОЗ($C15;$B$3:$B$8); G$12+1), скопируем формулу с ячейки E15 до ячейки Е35.
В ячейку F15 введем формулу
=ИНДЕКС($B$3:$F$8;ПОИСКПОЗ($D15;$B$3:$B$8);5), скопируем формулу с ячейки F15 до ячейки F35.
В ячейку G15 введем формулу =E15+F15, скопируем формулу с ячейки G15 до ячейки G35.
Находим максимальное значение для каждого состояния от 0 до 5, для этого в ячейку Н15 введем формулу =МАКС(G15), после копирования формулы в ячейку H16, необходимо изменить диапазон с G16 на G16:G17, для этого стоя в строке формул необходимо растянуть выделенный прямоугольник на одну ячейку вниз. Затем копируем формулу из H16 в ячейку H18 и проводим такие же операции по увеличению диапазона, и т.д. до ячейки H30.
Находим значение управления Хk, которому соответствует максимальное значение функции Zk, для этого в ячейку I15 введем формулу =ИНДЕКС($C15:G15;ПОИСКПОЗ(H15;G15;0);1), скопируем формулу в ячейки I16, I18, I21, I25, I30 постепенно увеличивая диапазон, аналогично тому, как это делалось в пункте 5. В результате получим следующую таблицу:
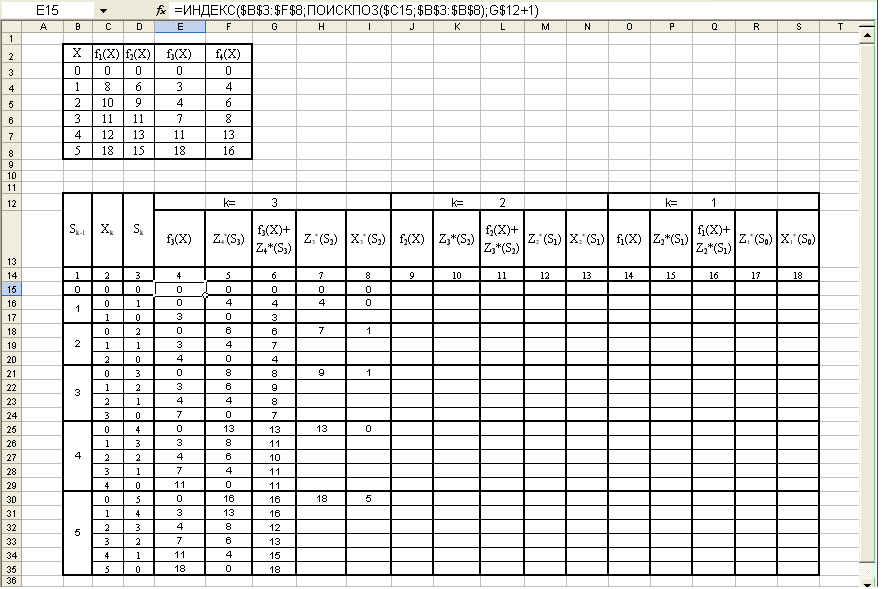
Выделяем диапазон ячеек E15:I35 выполняем команду Копировать, устанавливаем курсор в ячейку J15 выполняем команду Вставить.
Изменим формулу функции Z3*(S2). В ячейки K15, K16, K18, K21, K25, K30, введем соответственно максимальные значения предыдущего шага, находящиеся в ячейках H15, H16, H18, H21, H25, H30. В остальные ячейки поместим значения, стоящие в этом же столбце и соответствующие предыдущим Sk. В ячейку K17 копируем значение ячейки K15; в ячейки K19 и K20 – значения K16 и K17; в K22:K24 – K18:K20 и т. д. до ячейки K35. В результате получим:
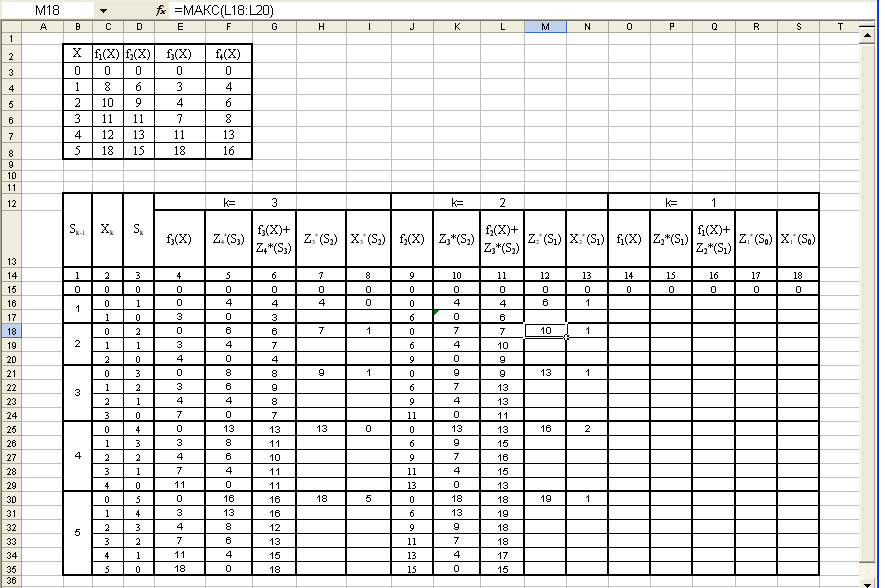
Выделяем диапазон ячеек J15:N35 выполняем команду Копировать, устанавливаем курсор в ячейку O15 выполняем команду Вставить. В результате получаем заполненную таблицу:
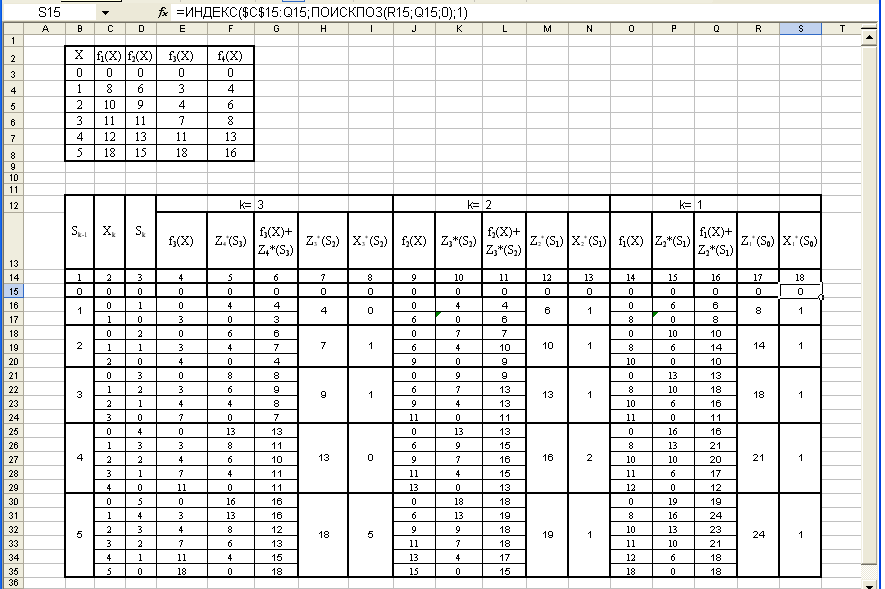
Сравнивая полученные значения, получим Z1*(5)=24 усл. ед. = Zmax при X1*= X1*(5)=1. Вычисляя, получим S1* = 5 - 1 = 4, а по таблице в столбце 12 находим X2* = X2* (4) = 2. Далее находим S2* = 4-2 = 2, а в столбце 6 X3* = X3*(2) = 1. Наконец, S3* = 2-1 = 1 и X4* = X4*(1) = 1, т. е. X*(1; 2; 1; 1).
Максимум суммарной прибыли равен 24 усл. ед. средств при условии, что 1-му предприятию выделено 1 усл. ед.; 2-му предприятию – 2 усл. ед.; 3-му предприятию – 1 усл. ед.; 4-му предприятию – 1 усл. ед.
ГЛОССАРИЙ
-
ЭММ
– экономико-математическая модель
ЛП
– линейное программирование
ЗЛП
– задача линейного программирования
ЗЦЛП
– задача целочисленного линейного программирования
ЭТ
– электронные таблицы
НЛП
– нелинейное программирование
ВП
– выпуклое программирование
ЦФ
ТИ
– целевая функция
– теория игр



– копировать
– вставить
– мастер функций
– автосумма
СМО – система массового обслуживания
СПУ – сетевое планирование и управление

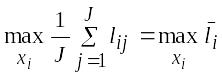 Если неизвестны
состояния среды, то все состояния
среды считают равновероятными:
Если неизвестны
состояния среды, то все состояния
среды считают равновероятными: