
- •5 Усилители радиосигналов (урс)
- •Качественные показатели урч
- •Коэффициент устойчивого усиления
- •Урс на полевых и биполярных транзисторах
- •Каскодная схема урс.
- •Многокаскадные урс.
- •Урс с одиночными настроенными контурами
- •Урс с попарно-расстроенными контурами
- •Многокаскадные урс с двухконтурными фильтрами
- •Бесконтурные урс
- •Узкополосные урс с сосредоточенной избирательностью
- •Урс диапазона свч
- •Общая теория урс свч
- •Внешние параметры урс
- •Усилители свч на биполярных и полевых транзисторах
- •Урс отражательного типа.
- •Усилители радиосигналов на туннельных диодах
- •Цепи с переменными параметрами (параметрические цепи)
- •Емкостные параметрические усилители
Урс с попарно-расстроенными контурами
Структурная схема УРС
соответствует рис.5.18. Входной и выходной
контуры в отличие от предыдущего случая
принудительно расстраиваются относительно
центральной частоты вверх и вниз на
некоторую величину, соответствующую
изменению обобщенной расстройки на
![]() .
Коэффициенты передачи каскадов одной
такой пары равны
.
Коэффициенты передачи каскадов одной
такой пары равны
![]() (5.37)
(5.37)
![]() .
(5.38)
.
(5.38)
Суммарный коэффициент передачи одной пары представляет собой произведение (5.37) и (5.38):
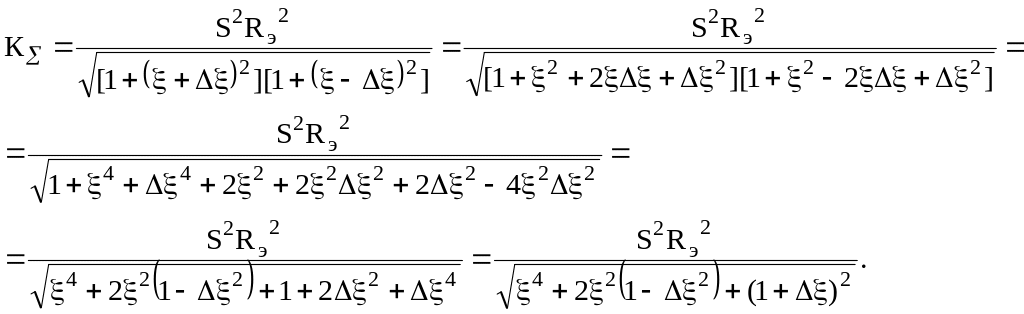
Анализ суммарной АЧХ одной такой пары показывает наличие нескольких характерных точек (рис.5.23), для которых
![]() .
(5.39)
.
(5.39)
Решением уравнения (5.39) являются следующие значения обобщенной расстройки:
![]()
Значение Δξ=1 соответствует критической расстройке, при которой провал на АЧХ отсутствует (максимально плоская АЧХ). При расстройке больше критической из-за деформации частотных характеристик (АЧХ и ФЧХ) происходит появление линейных искажений полезного сигнала.
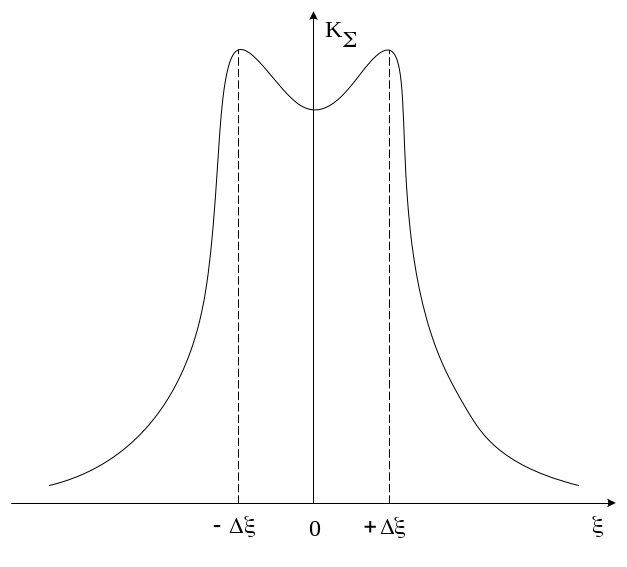
Рис.5.23
При Δξ=1 для суммарного коэффициента передачи одной пары получаем
 .
.
Фиксированный уровень γ для УРС, состоящего из n пар каскадов, равен
![]() ,
(5.40)
,
(5.40)
откуда значение обобщенной расстройки , которая необходима для получения уровня γ равно
![]()
Для уровня 0,707
![]() ,
,
следовательно, коэффициент прямоугольности многокаскадного УРС равен
 .
(5.41)
.
(5.41)
При
n=∞
и γ=0,01 предельное значение
![]() (рис.5.24).
(рис.5.24).

Рис.5.24
График зависимости резонансного коэффициента передачи многокаскадного УРС, который определяется в соответствии с выражением
 (5.42)
(5.42)
также имеет экстремальный характер при некотором значении числа каскадов m. При этом в отличие от резонансного многокаскадного УРС коэффициент передачи с ростом числа каскадов возрастает значительно быстрее: при m=4 (m=2n) и К1 =4 суммарный коэффициент передачи равен примерно 106, а экстремум имеет место при nopt=65 (рис.5.25).
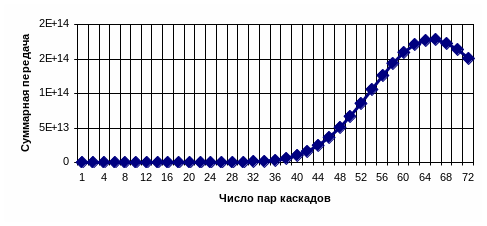
Рис.5.25
Многокаскадные урс с двухконтурными фильтрами
В усилительных каскадах УРС данного типа в качестве нагрузки применяются системы связанных колебательных контуров (рис.5.26).
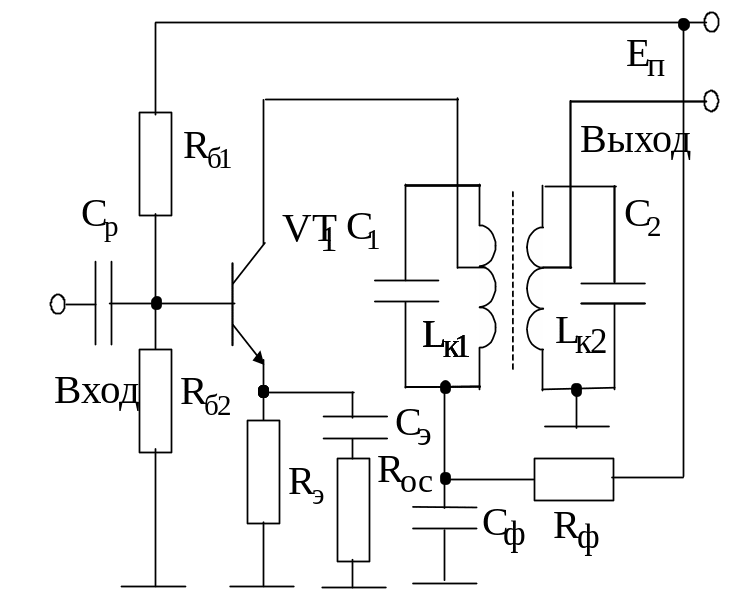
Рис.5.26
На рис.5.27 приведены контуры с различными видами связи.
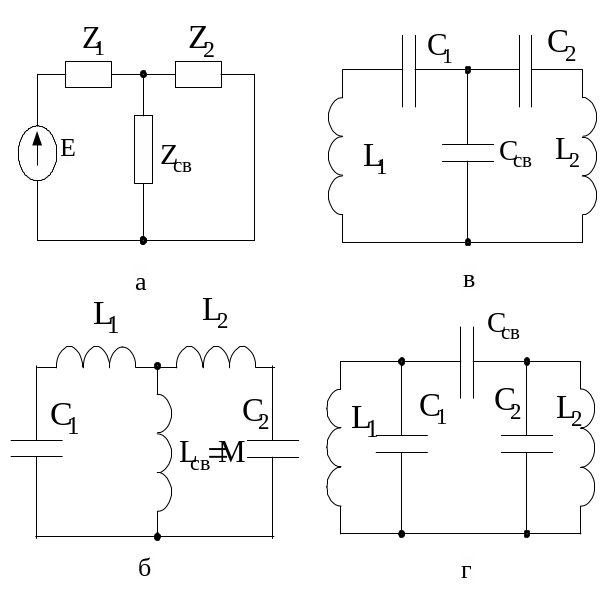
Рис.5.27. Обобщенная эквивалентная схема двух связанных контуров (а), контуры с индуктивной (б), внутриемкостной (в) и внешнеемкостной (г) связями
Наличие реактивного элемента
связи
![]() приводит к появлению дополнительных
активных и реактивных составляющих,
вносимых в первый контур из второго и
во второй контур из первого. Величина
этих дополнительных составляющих
определяется в соответствии с выражениями:
приводит к появлению дополнительных
активных и реактивных составляющих,
вносимых в первый контур из второго и
во второй контур из первого. Величина
этих дополнительных составляющих
определяется в соответствии с выражениями:
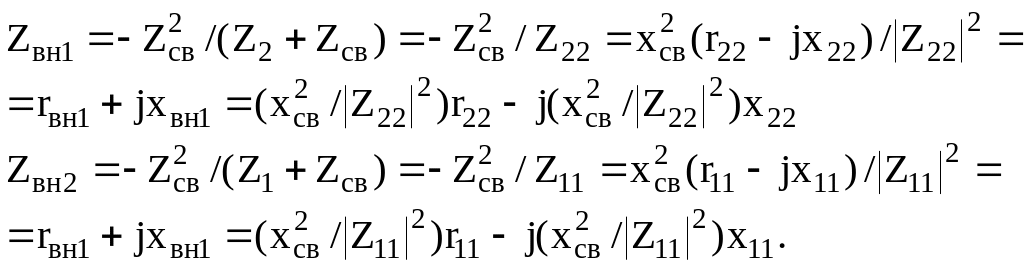
Из одного контура в другой
всегда вносится положительное активное
сопротивление и реактивное сопротивление
противоположного знака по сравнению с
реактивным сопротивлением контура, из
которого сопротивление вносится. Связь
между контурами оценивается коэффициентом
связи
![]() ,
где
,
где
![]() - степени связи:
- степени связи:
![]()
Следовательно
![]()
При индуктивной связи
(рис.5.27,б)
![]() .
При внутриемкостной связи (рис.5.27,в)
.
При внутриемкостной связи (рис.5.27,в)
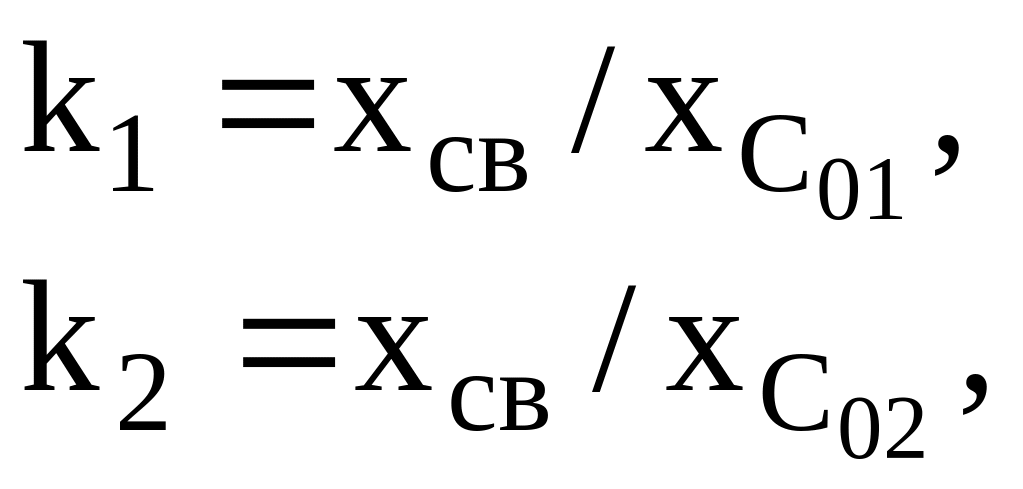
где
![]()
Тогда при слабой внутриемкостной
связи (![]() )
)
![]() .
При слабой внешнеемкостной связи
(рис.5.27,г)
.
При слабой внешнеемкостной связи
(рис.5.27,г)
![]() .
.
Для УРС с нагрузкой в виде индуктивно-связанных контуров (рис.5.26) комплексный коэффициент усиления равен:
![]()
где
![]() - обобщенная расстройка,
- обобщенная расстройка,
![]() - параметр связи между
контурами,
- параметр связи между
контурами,
![]() - коэффициент связи,
- коэффициент связи,
M - взаимная индуктивность между катушками контуров.
При равных эквивалентных
затуханиях контуров
![]() выражение принимает вид
выражение принимает вид
 (5.43)
(5.43)
Фазовая характеристика рассматриваемого усилителя равна:
![]() (5.44)
(5.44)
В зависимости от степени связи контуров различают:
слабую
связь,
![]() ,
при которой наблюдается один максимум
на нормированной АЧХ на частоте
,
при которой наблюдается один максимум
на нормированной АЧХ на частоте
![]() ;
;
критическую
связь,
![]() ,
при которой наблюдается максимально
плоская вершина АЧХ и один максимум на
частоте
;
,
при которой наблюдается максимально
плоская вершина АЧХ и один максимум на
частоте
;
сильную
связь,
![]() ,
при которой на АЧХ наблюдаются два
максимума на частотах
,
при которой на АЧХ наблюдаются два
максимума на частотах
![]() и один минимум на частоте
(рис.5.27).
и один минимум на частоте
(рис.5.27).
Вариант УРС с емкостной связью контуров представлен на рис.5.28.
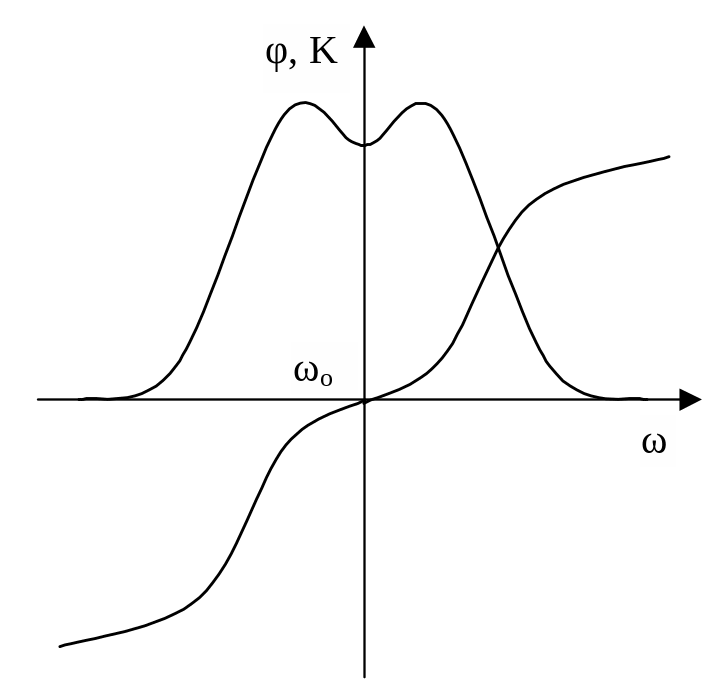
Рис.5.27. АЧХ и ФЧХ УРС со связанной парой контуров

Рис.5.28. УРС с емкостной связью контуров
При критической связи и полном включении контуров (m1=m2=1)
![]() (5.45)
(5.45)
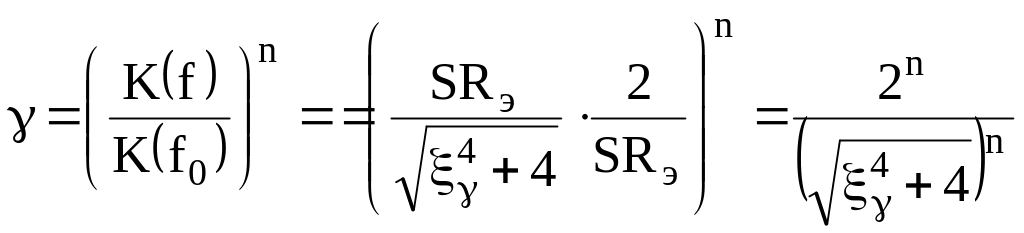 .
(5.46)
.
(5.46)
Выражение (5.46) совпадает с (5.40), следовательно, здесь справедливы рассмотренные ранее соотношения для коэффициента прямоугольности. Суммарный коэффициент передачи определяется в соответствии с выражением

и при К1=4 и n=4 равен примерно 12 (рис.5.29).
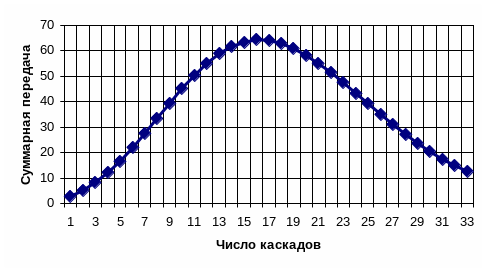
Рис.5.29
