
- •3 Пример расчета лестничной площадки марки лп 25.12-4к по серии 1.152.1-8
- •3.1 Исходные данные
- •3.2 Расчет плиты
- •3.3 Расчет лобового ребра
- •3.3.1 Расчет рабочей арматуры лобового ребра
- •3.3.2 Расчет наклонного сечения лобового ребра на действие поперечной силы
- •3.4 Расчет продольного пристенного ребра
- •3.4.1 Расчет рабочей арматуры пристенного ребра
- •3.4.2 Расчет наклонного сечения пристенного ребра на действие поперечной силы
3.3.2 Расчет наклонного сечения лобового ребра на действие поперечной силы
Поперечная сила от полной расчетной
нагрузки
![]() =25,47
кН с учетом коэффициента
=0,95:
=25,47
кН с учетом коэффициента
=0,95:
![]() =25,47∙0,95=24,20кН.
=25,47∙0,95=24,20кН.
Расчет производится на основе расчетной модели наклонных сечений.
Проверяем прочность ребра по наклонной полосе между наклонными трещинами в соответствии с условием:
![]() (3.13)
(3.13)
где
![]()
![]() ;
;
Отношение модулей упругости

где
![]() =0,9∙31∙103МПа
– модуль упругости бетона класса С
=0,9∙31∙103МПа
– модуль упругости бетона класса С![]() марки П1,П2 по удобоукладываемости,
подвергнутого тепловой обработке.
марки П1,П2 по удобоукладываемости,
подвергнутого тепловой обработке.
![]() =20∙104МПа
– модуль упругости арматуры.
=20∙104МПа
– модуль упругости арматуры.
![]() =20∙104/27,9∙103=7,17;
=20∙104/27,9∙103=7,17;
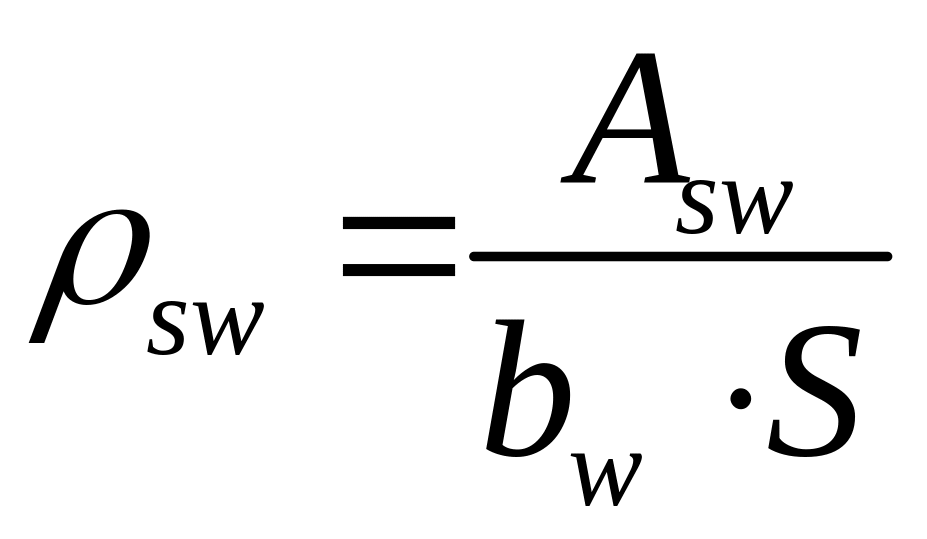 (3.14)
(3.14)
где
![]() =25,1
мм2 – площадь сечения двух
поперечных сечений стержней диаметром
4 мм из арматуры класса S500.
=25,1
мм2 – площадь сечения двух
поперечных сечений стержней диаметром
4 мм из арматуры класса S500.
![]() =115мм
– ширина ребра расчетного сечения.
=115мм
– ширина ребра расчетного сечения.
![]() -
шаг поперечных стержней каркасов Кр-1
лобового ребра.
-
шаг поперечных стержней каркасов Кр-1
лобового ребра.
![]() ,
принимаем S=150мм.
,
принимаем S=150мм.
![]() =25,1/(115∙150)=0,0015>
=25,1/(115∙150)=0,0015>![]() =
=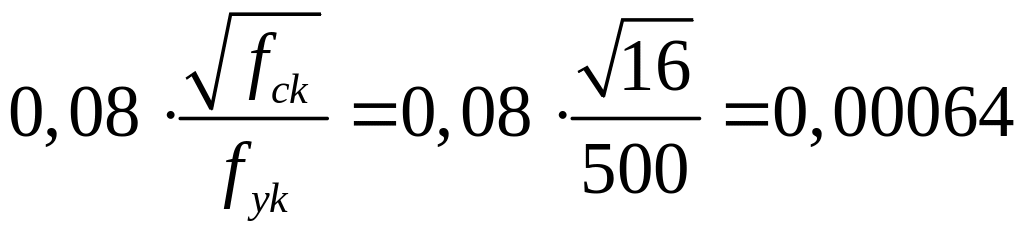 ;
;
![]() определено по пункту 11.2.5 [6].
определено по пункту 11.2.5 [6].
![]() =1+5∙7,17∙0,0015=1,054
< 1,3
=1+5∙7,17∙0,0015=1,054
< 1,3
![]() - коэффициент, определяемый по формуле:
- коэффициент, определяемый по формуле:
![]() (3.15)
(3.15)
где
![]() - коэффициент, принимаемый для тяжелого
бетона равным 0,01;
- коэффициент, принимаемый для тяжелого
бетона равным 0,01;
=1 – 0,01∙10,67=0,893.
Уточняем значение d:
d=300-(25+12/2)=269 мм.
![]() =0,3∙1,054∙0,893∙10,67∙115∙269=93203
Н =93,203 кН.
=0,3∙1,054∙0,893∙10,67∙115∙269=93203
Н =93,203 кН.
![]() =24,20кН
<
=93,203
кН.
=24,20кН
<
=93,203
кН.
Следовательно, прочность по наклонной полосе между наклонными трещинами обеспечена.
Определим поперечную силу, воспринимаемую бетоном и поперечной арматурой:
![]() (3.16)
(3.16)
![]() - коэффициент, принимаемый для тяжелого
бетона равным 2,0, учитывает влияние вида
бетона;
- коэффициент, принимаемый для тяжелого
бетона равным 2,0, учитывает влияние вида
бетона;
![]() - коэффициент, учитывающий влияние
сжатых полок в тавровых и двутавровых
элементах и определяется:
- коэффициент, учитывающий влияние
сжатых полок в тавровых и двутавровых
элементах и определяется:
 (3.17)
(3.17)
При этом
![]() :
550 – 115=435мм > 3∙70=210мм
:
550 – 115=435мм > 3∙70=210мм
Для расчета принимаем
![]() =210
мм;
=210
мм;
![]() =0,75∙210∙70/(115∙269)=0,36
< 0,5.
=0,75∙210∙70/(115∙269)=0,36
< 0,5.
![]() - коэффициент, учитывающий влияние
продольных сил, при отсутствии продольных
сил
=0.
- коэффициент, учитывающий влияние
продольных сил, при отсутствии продольных
сил
=0.
1+ + =1+0,36+0 =1,36 < 1,5
![]() -
усилие в поперечных стержнях на единицу
длины элемента:
-
усилие в поперечных стержнях на единицу
длины элемента:
 (3.18)
(3.18)
где
![]() =333МПа
– расчетное сопротивление поперечной
арматуры по таблице 6.5 [7].
=333МПа
– расчетное сопротивление поперечной
арматуры по таблице 6.5 [7].
![]() ;
;
![]() =66123Н=66,123кН.
=66123Н=66,123кН.
=24,20кН
<
![]() =66,123
кН.
=66,123
кН.
Следовательно, прочность на действие поперечной силы по наклонной трещине обеспечена.
3.4 Расчет продольного пристенного ребра
Подсчет нагрузки на 1м длины пристенного ребра приведен в таблице 3.3.
Таблица 3.3-Нагрузки на 1 м длины пристенного ребра
в кН/м2
Вид нагрузки |
Нормативная нагрузка |
Частный коэффициент безопасности по нагрузке, ,𝛾-𝑓. |
Расчетная нагрузка |
1 |
2 |
3 |
4 |
1. Постоянная 1.1 Собственный вес ребра
|
|
1,35
|
|
1.2 Собственный вес плиты
|
|
1,35 |
|
Итого постоянная
|
|
|
|
2. Переменная
|
1,83 |
1,5 |
2,745 |
Полная |
|
|
|
Расчетная схема пристенного ребра показана на рисунке 3.5:

Рисунок 3.5 – Расчетная схема пристенного ребра
Высота расчетного сечения h=220 – 20=200 мм;
Толщина сжатой полки =90-20=70 мм.
Толщина ребра
![]() ;
;
ширина растянутой полки
![]() .
.
Усилия от полной расчетной нагрузки:
- изгибающий момент:
 (3.19)
(3.19)

- поперечная сила:
![]() (3.20)
(3.20)
![]()


