Глава 4. Системы одновременных уравнений

4.1. Системы одновременных уравнений: основные понятия и примеры

Для описания многих сложных экономических процессов с целью большего приближения к реальности часто используется не одно уравнение, а целая система уравнений, отражающих наиболее существенные взаимосвязи (функциональные или статистические) между отдельными показателями. При этом в различных регрессионных уравнениях системы одни и те же переменные могут одновременно выступать, с одной стороны, в роли результирующих, объясняемых переменных, а с другой стороны - в роли объясняющих переменных. Такие системы уравнений обычно называют системами одновременных уравнений или эконометрическими (в узком смысле) моделями. Приведем примеры таких систем.

Пример 4.1. Модель спроса и предложения.

Как известно, в рыночной экономике спрос и предложение на некоторый продукт зависят от его цены. Силы рыночного механизма формируют цену таким образом, что спрос и предложение уравниваются. В предположении, что спрос и предложение в момент времени t являются линейными функциями от цены p_t в этот же момент времени, мы получаем следующую систему:

(4.1)

где ₀, ₁, ₀, ₁ - параметры модели, причем ₁<0, ₁>0; ₁, ₂ - случайные отклонения, наличие которых связано в первую очередь с отсутствием ряда важных объясняющих переменных, влияющих на спрос и предложение (дохода потребителей, цен сопутствующих товаров, налогов и т.д.).

Модель (4.1) может быть усовершенствована. Например, если в функцию спроса добавить доход потребителей y_t, то получим систему:

(4.2)

Пример 4.2. Модифицированная модель Кейнса.

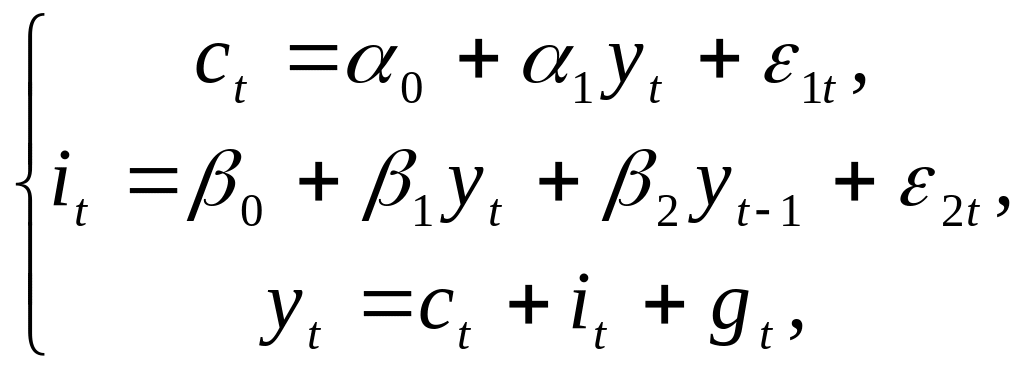(4.3.)

где с - расходы на потребление, y - ВВП, i - инвестиции, g - государственные расходы, t - текущий период, t-1 - предыдущий период.

В любой эконометрической модели в зависимости от конечных прикладных целей ее использования все участвующие в ней переменные подразделяются на:

экзогенные, т.е. задаваемые автономно, вне модели (их называют также независимыми, входными, управляющими переменными);

эндогенные, т.е. такие переменные, значения которых формируются внутри модели (другие названия - зависимые, выходные, результирующие переменные); общее число эндогенных переменных, как правило, совпадает с числом уравнений в системе;

предопределенные, т.е. экзогенные переменные и лаговые эндогенные переменные, значения которых входят в уравнения системы измеренными в прошлые (по отношению к текущему) моменты времени и, следовательно, являются уже известными, заданными.

Предопределенные переменные выступают в уравнениях системы в качестве объясняющих признаков-факторов. Так что, по существу, эконометрическая модель служит для прогнозирования эндогенных переменных в зависимости от значений предопределенных переменных.

Например, в модели спроса и предложения (4.1) эндогенными являются переменные , , p_t, а экзогенных и предопределенных переменных в ней нет. В модели (4.2) эндогенные переменные - те же, а единственной экзогенной переменной является y_t. Наконец, в модели (4.3): c_t, i_t, y_t - эндогенные переменные, g_t - экзогенная переменная, g_t и y_t-1 - предопределенные переменные.

Эконометрическая модель как система одновременных уравнений может быть представлена в структурной или приведенной форме.

В структурной форме ее уравнения имеют исходный вид, отражая непосредственные связи между переменными. При этом сами уравнения подразделяются на поведенческие уравнения и уравнения-тождества. В первых из них описываются взаимодействия между переменными. Во-вторых - соотношения, которые должны выполняться во всех случаях. Тождества не содержат подлежащие оценке параметры и случайные составляющие. Например, в системах (4.1)-(4.3) первые два уравнения поведенческие, а последние уравнения являются тождествами.

Приведенная форма получается после решения исходной модели относительно эндогенных переменных, выраженных только через экзогенные или предопределенные переменные, параметры модели, а также случайные составляющие.

Например, в модели (4.1), подставляя выражения для и в третье уравнение, последовательно получим представления для p_t, и через параметры и случайные составляющие. В результате приведенная форма модели (4.1) примет вид:

где - преобразованные случайные отклонения.

О том, с какой целью используется приведенная форма эконометрической модели, речь пойдет в следующем параграфе.