1.4.4. Определение среднего времени безотказной работы системы

Среднее время безотказной работы можно определить одним из следующих способов.

Способ 1. Найти аналитическое выражение для вероятности безотказной ра-

боты системы P_c(t) и воспользоваться формулой Т₁ = P_c(t)dt. Можно также

найти вероятность безотказной работы системы в преобразовании Лапласа

= P(t)e^-tsdt и воспользоваться соотношением Т₁ = .

Способ 2. Составить систему линейных алгебраических уравнений относи­тельно среднего времени τ₀ и τ₁ пребывания системы в состояниях (0) и (1) соответственно (см. рис. 1.2):

□ для схемы (а):

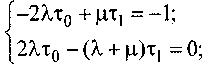(6.5)

□ для схемы (б);

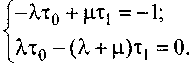(6.6)

Далее нужно решить полученные системы уравнений и определить среднее время безотказной работы по формуле Т₁ = τ₀ + τ₁.

Формулы для среднего времени безотказной работы имеют следующий вид:

□ для схемы (а):

□ для схемы (б):

где Т₀= — среднее время безотказной работы нерезервированной системы.

Сравнивая полученные значения среднего времени безотказной работы и на­работки на отказ, полученной в разд. 1.4.2, видим, что они практически одинаковы при малых значениях , что характерно для высоконадежных

систем.

1.4.5. Определение риска системы

Риском называется возможность потерь вследствие внутренних аномалий в системе или аномалий среды. В частности Техногенным риском называется возможность потерь из-за отказов техники. В большинстве случаев риск оценивается денежными единицами, хотя могут быть случаи, когда потери носят такой характер, что оценить их деньгами трудно или даже невозможно. Из определения следует, что риск является случайной величиной, вызванной двумя причинами: случайностью отказов и случайностью величины потерь. При расчетах используется его характеристика - математическое ожидание риска.

Риск системы определим по приближенной формуле (1.2). Для исходной не­резервированной системы при ρ = 0,01 получим:

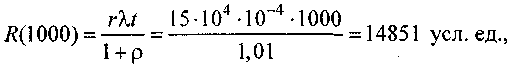
что выше допустимого.

Риск резервированной системы с кратностью m = 1 определяется по фор­мулам:

□ для постоянно включенного резерва:

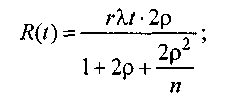
□ для резерва замещением:

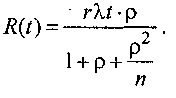
Результаты расчетов техногенного риска системы R(t) при t = 1000 час при различных видах резервирования и дисциплинах обслуживания сведены в

табл. 1.2. Из таблицы видно, что риск может быть меньше допустимого, рав­ного 360 усл. ед., при условии, что использован любой вид резервирования с кратностью т= 1 при ρ ≤ 0,01 и применяется обслуживание с любым при­оритетом. Для нашего случая обеспечить заданный риск можно при условии, что среднее время восстановления не будет превышать 100 часов.

Определим теперь величину риска в течение всего срока службы системы, равного 5 годам. По сравнению с R(1000) техногенный риск системы увеличится в = 43,8 раз и превысит требуемый риск, равный 360 усл. ед.

В заключение можно отметить, что исходная нерезервированная система не­достаточно надежна и не может обеспечить требуемый риск. Вероятность ее безотказной работы в течение 1000 часов равна 0,9, а риск равен 14851 усл. ед., что значительно выше требуемого (360 усл. ед.). В течение этого времени риск будет допустимым, если применить структурное резерви­рование любого вида кратности т = 1 и обеспечить обслуживание со средним временем восстановления не выше 100 часов.