1.3.2. Сравнительный анализ эффективности нагрузочного и структурного резервирования

Вероятность отказа Q_c(t) и среднее время безотказной работы Т_с системы при нагрузочном резервировании выражаются формулами:

Q_с(t) = 1- , Т_с = ,

где n — число, показывающее, во сколько раз уменьшается интенсивность отказа системы при наличии нагрузочного резервирования.

Тогда выигрыш надежности при структурном резервировании по сравнении с нагрузочным будет равен:

G_q(t) = 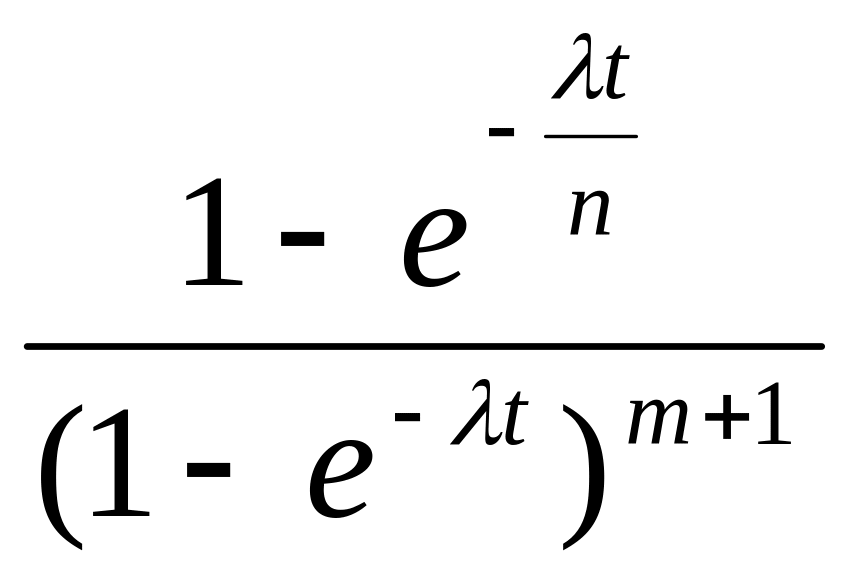(1.6)

Представим эту функцию в виде:

G_q(x,m,n)= (1.7)

Исследование выполним в такой последовательности:

- построить график функции G_q(x,m,n);

- определить критическое значение τ, характеризующее эффективность структурного резервирования по сравнению с нагрузочным.

По аналогии с описанным ранее введем функцию (1.7) и подставив с помощью кнопки SUB значения m=1, a n=2; 5; 10, получим следующие зависимости:

Графики функции G_q(x,m,n) построим с помощью кнопки 2D-plot window панели инструментов предварительно выделив соответствующие зависимости:

Подобрав соответствующий масштаб получим следующие графики:

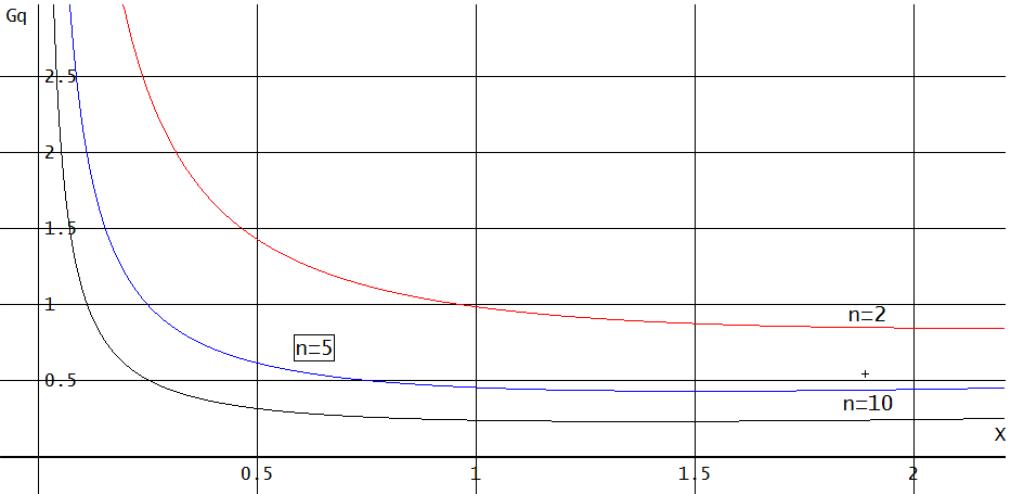
Рис. 1.3. Графики выигрыша надежности

Из графиков можно сделать следующие важные выводы:

- при малом времени работы системы целесообразно использовать струк­турное резервирование;

- область применения структурного резервирования тем шире, чем мень­ше n;

- критическое значение целесообразности структурного резервирования за­висит от его кратности т и величины нагрузочного резервирования п.

Из графика рис. 3.3 видно, что критическое значение τ тем больше, чем меньше п.

3.3.3. Исследование влияния последействия отказов

Рассмотрим следующую задачу: дана дублированная система; интенсивности отказа основной и резервной систем одинаковы и равны λ . При отказе одной из них нагрузка на исправную увеличивается и интенсивность отказа стано­вится равной > λ. Необходимо найти показатели надежности и оценить влияние последействия отказов. Задачу решим с помощью пакета Derive 6 в такой последовательности:

- получим формулы для вероятности и среднего времени безотказной рабо­ты, для чего введем формулу

P_c (t) = P ²(t) + 2 Q'(τ)P(τ)P₁(t-τ)d τ, (1.8)

где P(t) = ; P(τ)= ; Q'(τ)— производная от вероятности отказа

Q(τ)= 1 -Р(τ) ; P₁(t-τ) = .

Рекомендуется ввести первоначально составляющие формулы (1.8), а за­тем образовать подинтегральную формулу, оперируя номерами строк, которые при­своены составляющим:

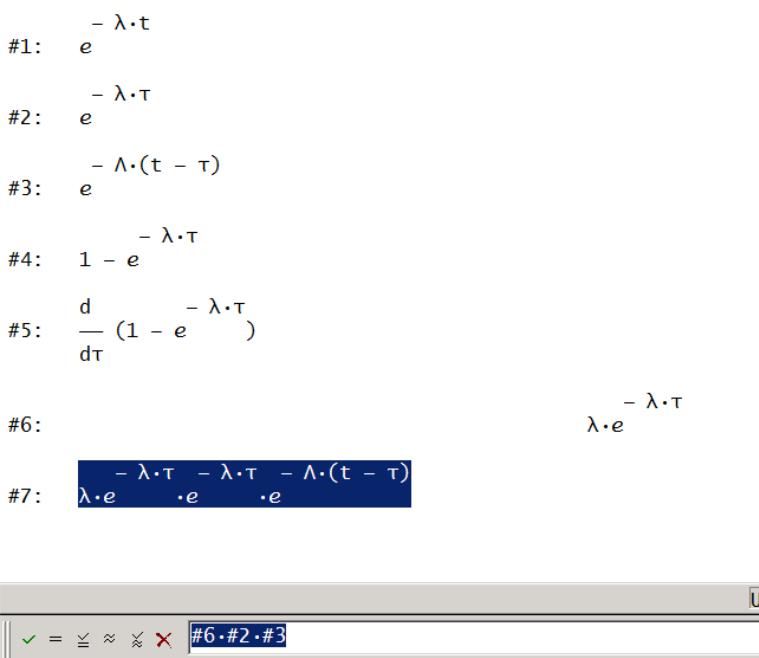
- найдем интеграл с помощью кнопки :

далее сформируем конечную формулу и нажав кнопку , получим формулу:

- найдем среднее время безотказной работы, вычислив интеграл от полу­ченного выражения для P_c(t) :

T= P_c(t)dt .

Для этого введем пределы изменения аргументов λ и Λ:

и используя кнопку получим формулу для Т:

Обратим внимание на формулу для P_c (t). Если Λ=2λ, то формула не имеет смысла;

- найдем аналогично предыдущему решение для (1.8), подставив Λ=2λ в составляющую P₁(t-τ);

- найдем новое значение среднего времени безотказной работы:

В результате решения получим следующие формулы:

P_c(t) = (l + 2λ t), T =

Анализ формул показывает, что последействие отказов может существенно снизить эффективность структурного резервирования. Так, например, если Λ=2λ, то среднее время безотказной работы резервированной системы бу­дет равно среднему времени безотказной работы нерезервированной систе­мы, т. е. резервирование не будет иметь смысла.