
- •Глава 6. Постановки задачи нелинейного программирования (знп) и основные определения…………………………...3
- •Глава 7. Задача одномерной оптимизации…………………………………….13
- •Глава 8. Графический метод решения знп…………………………………...33
- •Глава 10. Выпуклое программирование……………………………………....62
- •Глава 11. Квадратичное программирование…………………………………74
- •Глава 12. Задача безусловной оптимизации (збо)…………………………………………………………………..81
- •Глава 13. Задача условной оптимизации (зуо)……………………….……127
- •Глава 6.
- •6.1. Задача нелинейного программирования (знп) и ее постановки.
- •6.2. Основные определения.
- •6.3. Классификация знп.
- •6.4. Классическая оптимизация.
- •Глава 7. Методы одномерной оптимизации
- •Постановка задачи. Основные понятия
- •7.2. Поиск отрезка, содержащего точку максимума Алгоритм Свенна
- •Методы нулевого порядка.
- •Дихотомический поиск (метод деления отрезка пополам)
- •Метод золотого сечения
- •Метод дск-Пауэлла
- •7.4. Методы первого порядка.
- •Метод средней точки
- •Метод хорд (секущих)
- •Метод кубической аппроксимации
- •7.5. Методы второго порядка. Метод Ньютона-Рафсона
- •Итерация 1
- •Глава 8. Графический метод решения знп.
- •8.1. Алгоритм графического метода решения знп
- •8.2. Решение примеров.
- •Выпуклые и вогнутые функции
- •9.1. Определения
- •9.2. Свойства вогнутых (выпуклых) функций
- •9.3. Критерии вогнутости (выпуклости) гладких функций
- •9.4. Экстремальные свойства вогнутых (выпуклых) функций
- •9.5. Сильно вогнутые (выпуклые) функции
- •9.5.1. Определение. Примеры
- •9.5.2. Свойства сильно вогнутых (выпуклых) функций
- •9.5.3. Критерии сильной вогнутости (выпуклости)
- •9.5.4. Экстремальные свойства сильно вогнутых (выпуклых) функций
- •Глава 10. Выпуклое программирование
- •10.1. Постановка задачи
- •10.2. Функция Лагранжа. Седловая точка функции Лагранжа, условия ее существования Определение 10.1. Функция , (10.10)
- •10.3. Достаточные условия оптимальности
- •10.4. Условия регулярности выпуклого множества
- •10.5. Теорема Куна-Таккера. Общий случай
- •10.6. Теорема Куна-Таккера. Случай линейных ограничений
- •Глава 11. Квадратичное програмирование.
- •11.1. Постановка задачи квадратичного программирования (зкп)
- •11.2. Применение теории Куна-Таккера к решению зкп.
- •11.3. Решение задач.
- •Глава 12. Методы безусловной оптимизации
- •12.1. Постановка задачи
- •Алгоритм метода спуска
- •. Методы нулевого порядка (прямого поиска)
- •Метод Хука-Дживса
- •Алгоритм метода Хука-Дживса, использующий одномерный поиск
- •Метод покоординатного спуска
- •Первый вариант
- •Второй вариант
- •Методы первого и второго порядков
- •Градиентные методы. Метод скорейшего спуска – метод Коши
- •Метод Ньютона
- •Модифицированный метод Ньютона
- •Методы, использующие сопряженные направления
- •Определение сопряженных направлений
- •Оптимизация квадратичной функции. Конечная сходимость алгоритмов, использующих сопряженные направления
- •12.4.4. Метод Дэвидона-Флетчера-Пауэлла Шаг 1.Метод Дэвидона-Флетчера-Пауэлла (дфп) принадлежит к классу квазиньютоновских методов, в которых направление поиска задаётся в виде
- •Алгоритм метода дфп
- •Итерация 1
- •Шаг 2. Вычислим , тогда .
- •Шаг 2. Вычислим , тогда .
- •12.4.5. Метод сопряжённых градиентов Флетчера-Ривса
- •Алгоритм метода Флетчера-Ривса
- •Глава 13. Методы условной оптимизации
- •13.1. Постановка задачи. Классификация методов
- •Общая схема методов условной оптимизации
- •Шаг 2.Шаг 1. Выбрать ( -я итерация) – возможное направление подъёма функции в точке . Если такого направления нет, то - решение задачи. В противном случае перейти к шагу 2.
- •13.2. Методы возможных направлений
- •13.2.1. Метод Зойтендейка
- •Пример 13.2
- •Итерация 3
- •Шаг 4.Рисунок 13.6
- •13.2.2. Метод Топкиса-Вейнотта
- •Пример 13.3
- •Итерация 1
- •Шаг 5.Рисунок 13.7
- •Алгоритм метода Топкиса-Вейнотта
- •13.2.3. Метод Франка-Вульфа
- •Алгоритм метода Франка-Вульфа
- •Шаг 5. Находим шаг в направлении новой точки . Решение этой задачи (одномерной): .
- •Шаг 3. Так как , переходим к шагу 4.
- •Шаг 5. Решаем задачу: .
- •Литература
7.2. Поиск отрезка, содержащего точку максимума Алгоритм Свенна
Запишем
алгоритм для решения задачи
![]() .
.
Исходные
данные:
![]() -
начальная точка,
-
начальная точка,
![]() –
шаг поиска
–
шаг поиска
![]() .
.
Вычислить
 ;
;
 ;
;

 .
.Если
 ,
то
,
то
 ,
перейти к шагу 4.
,
перейти к шагу 4.Если
 ,
то
,
то
 ,
,
 ,
перейти к шагу 4, в противном случае
,
перейти к шагу 4, в противном случае

 ;
;
 ,
конец.
,
конец. ,
вычислить
,
вычислить
 .
.Если
 ,
то
,
то
 ,
перейти к шагу 4.
,
перейти к шагу 4.Если
 ,
то
,
то
 ;
;
 ,
конец, в противном случае
,
конец, в противном случае
 ;
;
 ,
конец.
,
конец.
Заметим,
что случай
![]() (шаг
3) не рассматривается, так как он
противоречит предположению об
унимодальности функции
.
(шаг
3) не рассматривается, так как он
противоречит предположению об
унимодальности функции
.
Для задачи минимизации алгоритм решения аналогичен.
Пример
7.1.
![]() ;
;
![]() ;
;
![]() .
.
K=1,![]() ;
;
![]() ;
;
![]() .
.
Поскольку
![]() ,
,
![]() ,
,![]() .
.
Далее
![]() .
.
K=2,
![]() ,
,
![]() ,
,![]() .
.
K=3,![]() ,
,
![]() ,
,![]() .
.
K=4,![]() ,
,
![]() ,
,![]() .
.
K=5,![]() ,
следовательно
,
следовательно
![]() ,
,![]() ;
;
![]() .
.
Таким
образом, мы получили интервал
![]() ,
в котором лежит точка x*.
,
в котором лежит точка x*.
Заметим, что эффективность поиска граничных точек непосредственно зависит от величины шага h. Если h велико, то получаем грубые оценки координат граничных точек, и построенный интервал оказывается весьма широким. С другой стороны, если h мало, для определения граничных точек может потребоваться достаточно большой объем вычислений.
Уменьшение длины отрезка, содержащего точку максимума, достигается путем последовательного исключения частей этого отрезка. Величина интервала, исключаемого на каждом шаге, зависит от расположения двух пробных точек внутри отрезка. Поскольку координата точки максимума априори неизвестна, целесообразно размещать пробные точки таким образом, чтобы обеспечивать уменьшение длины отрезка в одном и том же отношении.
После того как установлены границы интервала, содержащего точку оптимума, можно применить более сложную процедуру уменьшения интервала поиска с целью получения уточненных оценок координат оптимума. Величина подынтервала, исключаемого на каждом шаге, зависит от расположения пробных точек и внутри интервала поиска. Поскольку местонахождение точки оптимума априори неизвестно, целесообразно предположить, что размещение пробных точек должно обеспечивать уменьшение интервала в одном и том же отношении. Кроме того, в целях повышения эффективности алгоритма необходимо потребовать, чтобы указанное отношение было максимальным. Подобную стратегию иногда называют минимаксной стратегией поиска [4].
Методы нулевого порядка.
Дихотомический поиск (метод деления отрезка пополам)
Рассмотрим
задачу
![]()
Пробные точки y, z на каждом шаге этого метода выбираются следующим образом:
![]() ,
,
![]() ,
где
,
где
![]() -
параметр метода,
-
параметр метода,
![]() .
.
При
малых
каждая из пробных точек делит отрезок
![]() почти пополам, т.е. исключению будет
подлежать почти половина отрезка.
почти пополам, т.е. исключению будет
подлежать почти половина отрезка.
Алгоритм метода дихотомического поиска.
Исходные
данные.
Отрезок
,
содержащий точку максимума; параметр
и параметр окончания счета
![]()
![]() .
.
 ,
,
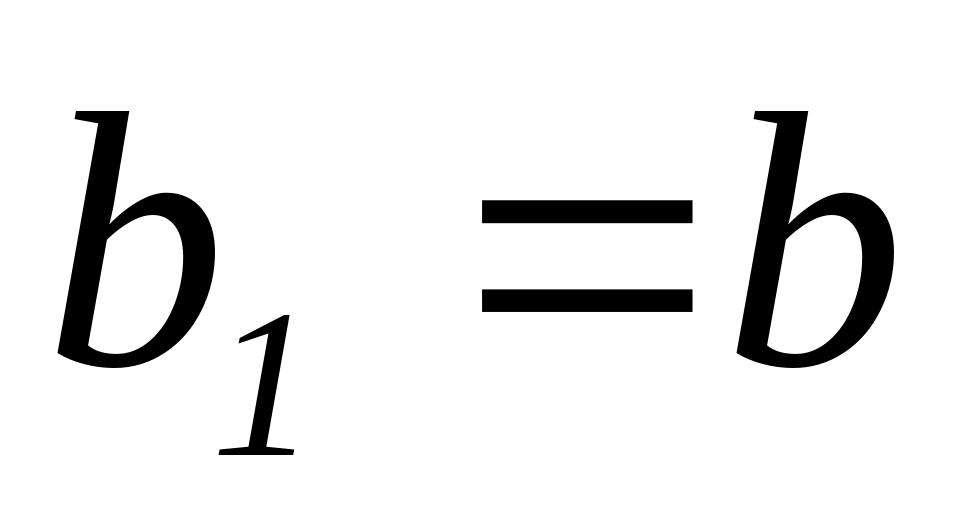 ,
,
 .
.Если
 ,
то
,
то
 ,
конец.
,
конец. ,
,
 ,
,
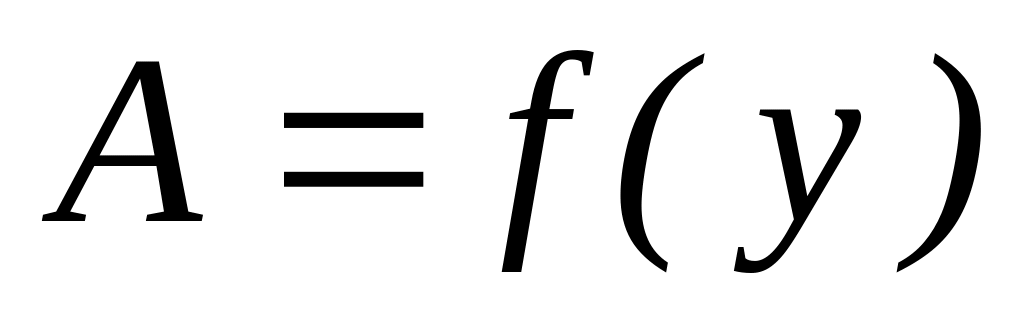 ,
,
 .
.Если
 ,
то
,
то
 ,
,
 ,
в противном случае
,
в противном случае
 ,
,
 .
., перейти к шагу 2.
Пример
7.2.
Найти точку максимума функции
![]() на отрезке
на отрезке
![]() ;
;
![]() ;
;
![]() .
.
Итерация
. k=1,
![]()
![]() ,
,
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
,
![]() ;
;
![]() .
.
Итерация 2
![]() ,
,
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
,
![]() ;
;
![]() .
.
Итерация 3
![]() ,
,
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
,
![]() ;
;
![]() .
.
Итерация 4
![]() ;
;
![]() .
.
Таким
образом, на каждой итерации дихотомического
поиска производится два вычисления
значения функции и после n
вычислений (n/2
итераций), длина начального интервала
уменьшается приблизительно в
![]() раз.
раз.
