1. Определение сопряженных направлений

Пусть – симметричная матрица порядка ; направления (векторы) называются – сопряженными, или просто сопряженными, если они:

1. линейно-независимы,

2. , .

На следующем примере иллюстрируется понятие сопряженности и значение сопряженных направлений для оптимизации квадратичных функций.

Пример 12.7. Найти точку минимума функции , используя сопряженные значения.

Очевидно, что оптимальной является точка , в которой . Построим сопряженные направления. Используя в качестве матрицы матрицу Гессе функции . Пусть . Тогда вектор должен удовлетворять равенству , где – матрица Гессе . Так как , то , или . В частности, если , то . Векторы и – линейно-независимы. Уже из данного примера, очевидно, что сопряженные направления выбираются неоднозначно. Для решения поставленной задачи проделаем две итерации.

Итерация 1

1. Выберем в качестве начальной точки произвольную точку, например .

2. Определим ; .

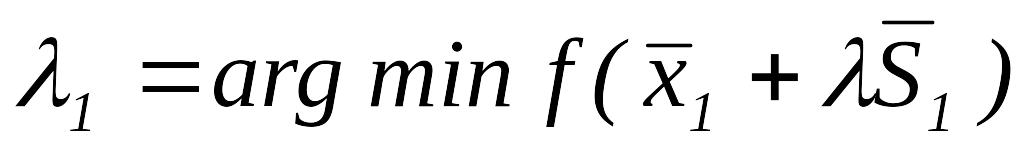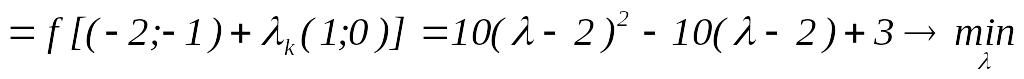Очевидно, что , следовательно, .

Итерация 2

2. Определим ; .

Очевидно, что .

Данный пример показывает, что оптимум квадратичной функции может быть не более чем за шагов ( одномерных поисков, в примере ) при условии, что поиск ведется вдоль направлений, сопряженных относительно матрицы Гессе данной функции.

Пример 12.8. Привести квадратичную функцию из примера 12.7 к каноническому виду (к сумме полных квадратов).

.

Рассмотрим преобразование

, или , .

В матричной форме .

В преобразованном виде квадратичная функция принимает вид .

Рассмотрим матрицу преобразований .

Очевидно, что ее столбцы и с точностью до множителя совпадают с построенными в примере 12.7 сопряженными относительно матрицы Гессе направлениями и .

Таким образом, если известна матрица – преобразования исходной квадратичной функции, то оптимум квадратичной функции может быть найден не более чем за шагов ( одномерных поисков), при условии, что поиск ведется вдоль направлений, задаваемых столбцами матрицы .

2. Оптимизация квадратичной функции. Конечная сходимость алгоритмов, использующих сопряженные направления

Рассмотрим задачу безусловной оптимизации квадратичной функции

, (12.11)

где , , – симметричная матрица порядка .

Задачи оптимизации квадратичных функций занимают важное место в теории оптимизации в силу следующих причин:

1. Квадратичная функция представляет собой простейший тип нелинейной функции, для которой может быть поставлена задача безусловной оптимизации.

2. Решение задачи безусловной оптимизации может быть получено не более чем за шагов при условии, что поиск ведется вдоль сопряженных относительно матрицы направлений.

3. Поскольку в окрестностях точки оптимума произвольную нелинейную функцию можно достаточно хорошо аппроксимировать квадратичной функцией, то естественно ожидать, что алгоритмы, использующие сопряженные направления, будут эффективны и для оптимизации неквадратичных функций.

Основная идея алгоритмов, использующих сопряженные направления, заключается в связи между построением указанных направлений и преобразованием квадратичных функций к виду полных квадратов.

Действительно, пусть известна матрица преобразований , которая приводит квадратичную функцию (12.12)

к каноническому виду.

Тогда , (12.13)

, (12.14)

где – соответствующая квадратичная форма,

– диагональная матрица и

. (12.15)

Пусть – -й столбец матрицы . Тогда в силу (2.15)

, (12.16)

так как – диагональная матрица. Таким образом, столбцы матрицы представляют собой искомые сопряженные направления. Если матрица известна, то матрица может быть найдена с помощью метода Жордана-Гаусса. Однако практически такой подход малопригоден и вообще невозможен, если речь идет о методах нулевого порядка, использующих только функции (матрица может быть неизвестна).

В данном разделе будут описаны несколько методов построения сопряженных относительно матрицы (или матрицы Гессе, если функция неквадратичная) направлений.

Прежде чем переходить к изложению конкретных методов, сформулируем теорему о конечной сходимости этих методов в случае квадратичных функций.

Теорема 12.1. Пусть задача (12.11) решается с помощью следующего алгоритма:

Начальный этап. Задать – произвольную начальную точку, – – сопряженные направления, положить .

Основной этап.

1. Определить , .

2. Положить ;

3. Если , то положить и перейти к шагу 1, иначе положить и остановится.

Тогда , где .

12.4.3. Метод Пауэлла – метод сопряжённых направлений нулевого порядка

Рассмотрим задачу (12.11) и метод её решения, предложенный Пауэллом в 1964 году. Метод Пауэлла представляет собой алгоритм построения системы сопряжённых направлений с использованием только значений целевой функции. Построение сопряжённых направлений основано на следующем свойстве квадратичных функций.

Теорема 12.2. Пусть - квадратичная функция, - две произвольные точки, - произвольное направление. Далее пусть и , . Тогда направление сопряжено с , т.е.

.

Пример 12.9. Найти точку минимума функции

,

используя теорему 12.2.

Пусть заданы точки и , и направление .

Шаг 1. Определим , .

Шаг 2. Определим , .

Шаг 3. Определим , где .

Шаг 4. Определим .

В данном случае минимум функции был найден с помощью трёх одномерных поисков (см. рис. 12.8).

Рисунок 12.8

На основании теоремы 12.2 можно строить сопряжённые направления, исходя из одной начальной точки и линейно-независимых направлений, например единичных координатных векторов . Так, в случае процедура оптимизации будет содержать одномерным поискам.

Шаг 1. Вычислить , .

Шаг 2. Вычислить , .

Шаг 3. Вычислить , .

Шаг 4. Определить - направление - сопряжённое в силу теоремы 2.2 с .

Шаг 5. Вычислить , .

Приведённый алгоритм построения сопряжённых направлений и нахождения оптимума квадратичных функций для легко обобщается.

Теорема 12.3. Пусть - точка, найденная в результате поиска из точки вдоль каждого из - сопряжённых направлений , а точка получена в результате поиска из точки вдоль те же направлений. Тогда направление сопряжено со всеми направлениями .

На рис. 12.9 показано построение системы сопряжённых направлений в случае , осуществлённое на основании теоремы 12.3.

Рисунок 12.9

Сначала осуществляется поиск вдоль трёх координатных направлений и снова вдоль (в общем случае - поиск). По теореме 12.3 направление сопряжено с . Затем проводятся опять четыре одномерных поиска вдоль и снова . По теореме 2.3 направление сопряжено с и . Таким образом, за две итерации ( в общем случае) построена система сопряжённых направлений . По направлениям и одномерный поиск уже сделан, осталось провести один поиск вдоль направления , в результате которого будет найдена точка - оптимальная. В общем случае алгоритм требует

(12.17)

одномерных поисков ( - итерация, состоящая из одномерного поиска, плюс последний одномерный поиск вдоль -го сопряжённого направления). Одна итерация отвечает построению одного направления, сопряжённого со всеми предыдущими направлениями.

Алгоритм метода сопряжённых направлений Пауэлла для оптимизации квадратичных функций

Начальный этап. Задать начальную точку и систему линейно-независимых направлений , (например, ), положить , .

Основной этап.

Шаг 1. Положить , , .

Шаг 2. Вычислить , .

Шаг 3. Если , то положить и перейти к шагу 2.

Шаг 4. Положить , .

Шаг 5. Если , то положить , , , , , и перейти к шагу 1.

Шаг 6. Вычислить , положить и остановиться.

Из теоремы 12.3 следует, что приведённый алгоритм генерирует сопряжённые направления. Для того чтобы воспользоваться теоремой 12.1, необходимо дополнить алгоритм Пауэлла процедурой проверки линейной независимости генерируемых алгоритмом направлений.

Пример 12.10. Найти точку минимума функции

методом Пауэлла.

Начальный этап. Пусть , , , , .

Основной этап.

Шаг 1. Положим , , .

Шаг 2. Вычислим , .

Шаг 3. Так как , то полагаем и переходим к шагу 2.

Шаг 2. Вычислим , .

Шаг 3. Так как , то полагаем и переходим к шагу 2.

Шаг 2. Вычислим , .

Шаг 3. Так как , то переходим к шагу 4.

Шаг 4. Положим , .

Шаг 5. Так как , то переходим к шагу 6.

Шаг 6. Вычислим , .

Последовательные шаги алгоритма представлены на рис. 12. 10. Легко также проверить, что направления и сопряжены по матрице

Рис. 12.10

Кроме того, очевидно, что преобразование, задаваемое матрицей

; ,

должно приводить исходную квадратичную функцию к каноническому виду. Действительно, , , тогда .

Метод Пауэлла, дополненный процедурой проверки сходимости и линейной независимости генерируемых направлений, можно применять для оптимизации неквадратичных функций, но при этом он не будет конечным.

2. Алгоритм метода Пауэлла для оптимизации неквадратичных функций

Начальный этап. Задать начальную точку , - параметр окончания счёта и систему линейно-независимых направлений , , положить , .

Основной этап.

Шаг 1. Положить , , .

Шаг 2. Вычислить , .

Шаг 3. Если , то положить и перейти к шагу 2.

Шаг 4. Положить , , , , .

Шаг 5. Если , то положить , , , перейти к шагу 1.

Шаг 6. Вычислить , .

Шаг 7. Если , то и остановиться, иначе положить , , и перейти к шагу 1.