
- •44. Фракталы, определение и примеры
- •43. Моделирование и подобие. Получение критериев подобия с помощью метода интегральных аналогов (пример с уравнением Навье-Стокса)
- •42. Моделирование и подобие; динамические аналогии; критерии подобия. Пи-теорема.
- •Компьютерные модели в автоматизированном управлении
- •40. Прямой метод Ляпунова
- •39. Подход к оценке устойчивости по линеаризованным уравнениям.
- •38. Определение устойчивости, устойчивость по Ляпунову
- •37. Инвариантность систем.
- •36. Управляемость и наблюдаемость
- •35.Представление в пространстве состояний и модель «вход-выход»
- •34. Единый подход к линеаризации.
- •33. Общая схема нечеткого вывода.
- •32. Нечеткое представление информации; типовые функции принадлежности, мера нечеткости.
- •31. Факторный анализ
- •30. Метод главных компонент
- •1.Среднее арифметическое переменных
- •7. Считаем дискриминантные функции
- •24. Непараметрическая статистика Манна-Уитни.
- •23. Составление статистических оценок ; анализ наиболее часто используемых законов распределения.
- •22. Составление статистической оценки на основе распределения Колмогорова – Смирнова.
- •21. Составление статистической оценки на основе распределения Фишера.
- •20. Составление статистических оценок ; анализ наиболее часто используемых законов распределения.
- •19. Общий подход к составлению статистических оценок
- •18. Проблема оценки адекватности моделей
- •17. Матричная форма мнк при построении модели (этап проверки адекватности полученной модели).
- •16. Матричная форма мнк при построении модели (этап проверки значимости коэффициентов модели).
- •15. Матричная форма мнк при построении модели (этап оценки коэффициентов модели).
- •13. Метод ранговой корреляции по Спирмэну.
- •12. Виды зависимостей. Корр анализ; коэффициенты частной и множественной корреляции.
- •11. Виды зависимостей. Корр анализ; коэфф парной корр-ии.
- •10.Метод наименьших квадратов - базовый метод получения коэффициентов регрессионных уравнений.
- •9.Виды зависимостей. Регрессионный анализ.
- •8. Классификация задач управления; задача оценивания.
- •Классификация задач управления; задача адаптивного управления
- •Классификация задач управления; задача детерминированного и стохастического управления.
- •Классификация задач управления. Задача идентификации.
- •3.Методология построения детерминированных моделей.
- •4.Основные виды зависимостей.
- •2. Общие подходы к построению моделей с учетом характера исходной информации.
- •Классификация моделей.
- •1. Дискретно - детерминированные модели
- •2. Непрерывно - детерминированные модели
- •3. Дискретно - стохастические модели
- •4. Непрерывно - стохастические модели
35.Представление в пространстве состояний и модель «вход-выход»
П редставление
в пространстве состояний.
dx/dt
=
Ax + Bu + Гd;
x(0)
– начальные условия
y
= Cx
x
- n-мерный вектор состояний; u
-
m-мерный вектор управления; d
-
k-мерный вектор возмущений; y
- l-мерный
вектор выхода;
А=[n´n]
Г=[n´k]
В=[n´m]
С=[l´n]
редставление
в пространстве состояний.
dx/dt
=
Ax + Bu + Гd;
x(0)
– начальные условия
y
= Cx
x
- n-мерный вектор состояний; u
-
m-мерный вектор управления; d
-
k-мерный вектор возмущений; y
- l-мерный
вектор выхода;
А=[n´n]
Г=[n´k]
В=[n´m]
С=[l´n]
Модель «выход-вход»

![]() -
частотная область
-
частотная область
L - преобразование Лапласа
Преобразование Лапласа - представление в частотной области . Обозначим: f(t) – оригинал; F(s)- изображение.
![]() -
одностороннее преобразование
Лапласа.
Условия, необходимые для
использования преобразования Лапласа:
1.
f(t)
непрерывна на интервале t
³
0,
непрерывность может быть нарушена
только лишь конечным числом разрывов
1-го рода.
2.
f(t) = 0
при t
< 0
3.
f(t)
не должна иметь неограниченного роста
-
одностороннее преобразование
Лапласа.
Условия, необходимые для
использования преобразования Лапласа:
1.
f(t)
непрерывна на интервале t
³
0,
непрерывность может быть нарушена
только лишь конечным числом разрывов
1-го рода.
2.
f(t) = 0
при t
< 0
3.
f(t)
не должна иметь неограниченного роста
По одной и той же передаточной функции можно построить целое семейство уравнений в пространстве состояний. Это происходит потому, что передаточная функция - это рациональная дробь, а числитель и знаменатель ее представлены в виде полиномов, часто имеющих общие корни. При сокращении нарушается эквивалентность представления. Условиям однозначного перехода от частотной области к временной является выполнение условий управляемости и наблюдаемости.
34. Единый подход к линеаризации.

Ф(x) - нелинейный элемент; Примеры нелинейных элементов.
1. Логистическая кривая, сигмоидальная
2.Характеристика зоны нечувствительности.
3. Гистерезис.
у=
Ф(x) -
нелинейная характеристика
![]() -
линеаризованная характеристика
1.
K(s)
- коэффициент статической линеаризации
2. K(d)
- коэффициент динамической (дифференциальной)
линеаризации
3. K(h)
- коэффициент гармонической линеаризации
4.
K(st)
- коэффициент статистической
линеаризации
Коэффициенты типа 1, 2
(k(s),
k(d))
y
= Ф(x)
-
линеаризованная характеристика
1.
K(s)
- коэффициент статической линеаризации
2. K(d)
- коэффициент динамической (дифференциальной)
линеаризации
3. K(h)
- коэффициент гармонической линеаризации
4.
K(st)
- коэффициент статистической
линеаризации
Коэффициенты типа 1, 2
(k(s),
k(d))
y
= Ф(x)
![]()
![]()
![]()
![]()
Коэффициенты типа 3 (k(h)) x(t) = Asin(wt) y =Ф(x)=Ф(Asin(wt))
![]()
![]()
а)
![]()
б)
![]()
![]()
![]()
а)
![]() ;
б)
;
б)
![]()
![]()
![]()
![]()
Используется при создании нелинейных систем уравнений. Коэффициент k(st)

![]() где
x(t)
- случайный процесс
где
x(t)
- случайный процесс
![]()
![]()
![]()
![]()
![]()
![]()
33. Общая схема нечеткого вывода.
Нечеткие правила вывода.
Базовое правило вывода типа "если - то" (англ.: if - then rule) называется также нечеткой импликацией, принимающей форму если x это A, то y это B , где А и В - это лингвистические значения, идентифицированные нечетким способом через соответствующие функции принадлежности для переменных х и у. Часть "х это А" называется условием (предпосылкой), а "у это В" - следствием (заключением).
Нечеткое рассуждение - это процедура, которая позволяет определить заключение, вытекающее из множества правил "если - то".
Такое множество при N переменных Xi может принять вид: если X1 это A1 и X2 это A2 …. и Xn это An, то y это B ,
Структура нечеткой системы с фуззификатором и дефуззификатором.
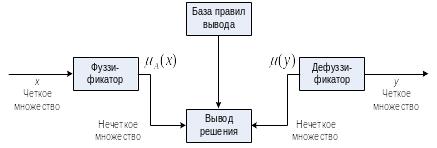
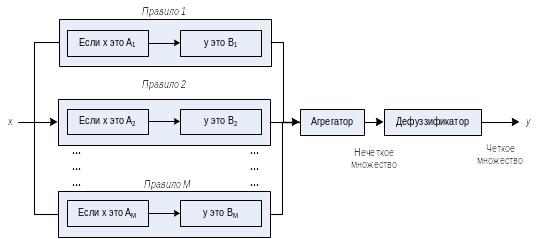
Организация вывода в нечеткой системе при наличии M правил вывода.
Основные этапы нечеткого вывода
Диаграмма деятельности процесса нечеткого вывода.
 =>
формирование базы правил => фаззификация
входных переменных => агрегирование
подусловий => активизация подзаключений
=> аккумулирование заключений =>
=>
формирование базы правил => фаззификация
входных переменных => агрегирование
подусловий => активизация подзаключений
=> аккумулирование заключений =>
Формирование базы правил систем нечеткого вывода.
База правил систем нечеткого вывода предназначена для формального представления эмпирических знаний или знаний экспертов в той или иной проблемной области.
В системах нечеткого вывода используются правила нечетких продукций, в которых условия и заключения сформулированы в терминах нечетких лингвистических высказываний рассмотренных выше видов.
Совокупность таких правил называется базами правил нечетких продукций.
