
- •44. Фракталы, определение и примеры
- •43. Моделирование и подобие. Получение критериев подобия с помощью метода интегральных аналогов (пример с уравнением Навье-Стокса)
- •42. Моделирование и подобие; динамические аналогии; критерии подобия. Пи-теорема.
- •Компьютерные модели в автоматизированном управлении
- •40. Прямой метод Ляпунова
- •39. Подход к оценке устойчивости по линеаризованным уравнениям.
- •38. Определение устойчивости, устойчивость по Ляпунову
- •37. Инвариантность систем.
- •36. Управляемость и наблюдаемость
- •35.Представление в пространстве состояний и модель «вход-выход»
- •34. Единый подход к линеаризации.
- •33. Общая схема нечеткого вывода.
- •32. Нечеткое представление информации; типовые функции принадлежности, мера нечеткости.
- •31. Факторный анализ
- •30. Метод главных компонент
- •1.Среднее арифметическое переменных
- •7. Считаем дискриминантные функции
- •24. Непараметрическая статистика Манна-Уитни.
- •23. Составление статистических оценок ; анализ наиболее часто используемых законов распределения.
- •22. Составление статистической оценки на основе распределения Колмогорова – Смирнова.
- •21. Составление статистической оценки на основе распределения Фишера.
- •20. Составление статистических оценок ; анализ наиболее часто используемых законов распределения.
- •19. Общий подход к составлению статистических оценок
- •18. Проблема оценки адекватности моделей
- •17. Матричная форма мнк при построении модели (этап проверки адекватности полученной модели).
- •16. Матричная форма мнк при построении модели (этап проверки значимости коэффициентов модели).
- •15. Матричная форма мнк при построении модели (этап оценки коэффициентов модели).
- •13. Метод ранговой корреляции по Спирмэну.
- •12. Виды зависимостей. Корр анализ; коэффициенты частной и множественной корреляции.
- •11. Виды зависимостей. Корр анализ; коэфф парной корр-ии.
- •10.Метод наименьших квадратов - базовый метод получения коэффициентов регрессионных уравнений.
- •9.Виды зависимостей. Регрессионный анализ.
- •8. Классификация задач управления; задача оценивания.
- •Классификация задач управления; задача адаптивного управления
- •Классификация задач управления; задача детерминированного и стохастического управления.
- •Классификация задач управления. Задача идентификации.
- •3.Методология построения детерминированных моделей.
- •4.Основные виды зависимостей.
- •2. Общие подходы к построению моделей с учетом характера исходной информации.
- •Классификация моделей.
- •1. Дискретно - детерминированные модели
- •2. Непрерывно - детерминированные модели
- •3. Дискретно - стохастические модели
- •4. Непрерывно - стохастические модели
13. Метод ранговой корреляции по Спирмэну.
Для определения взаимозависимости между переменными, имеющими произвольное двумерное непрерывное распределение, можно пользоваться коэффициентов ранговой корреляции спирмена. Ряды измерений xi и yi I = 1,2,3…n , преобразуется с помощью рангов следующим образом. Каждому значению x1 ставится в соответствии ранг R1 , т.е. номер элемента x1 в вариационном ряду; аналогичным образом определяется ранги остальных элементов.

12. Виды зависимостей. Корр анализ; коэффициенты частной и множественной корреляции.
Зависимость:1) Функциональная (функция, функционал, оператор)
2) Стохастическая (регрессия, корреляция)
Функционал совокупности функций ставит в соответствие совокупность чисел
Оператор Если заданы два произвольных множества Sx и Sy и дан закон, в соответствии с которым любому x будет соответствовать вполне определенный y , то говорят, что задан оператор. Функция, Функционал и Оператор – отражают действие причинно-следственной связи. Стохастическая связь - это такая зависимость, при которой определенному значению x будет соответствовать множество y. Корреляционный момент (ковариация) или момент связи Кху называют второй смешанный центральный момент, т.е. матем. ожидание произведения центрированных в-н
х°=x-mx и y°=y-my. Kxy=M[(x-mx)(y-my)] Коэффициентом корреляции случайных величин Х и У называется мат. ожидание произведения стандартных случайных величин rxy=M[((x-mx)/σx)((y-my)/σy)] rxy=Kxy/(σxσy) коэффициент корреляции характеризует степень тесноты линейной стохастической связи между случайными величинами
Корреляционный анализ изучает на основании выборки стохастическую зависимость между случайными переменными. Для коэффициента корреляции ρ двух случайных величин х и у справедливо: 1) -1≤ρ≤1 2) при ρ=±1 имеется функциональная связь, т.е. все точки лежат на прямой 3) если ρ=0, то х и у –некоррелированы (но это не говорит об отсутствии связи. Две независимые случайные переменные всегда некоррелированы, но некоррелированные переменные необязательно независимы) Параметр ρ оценивается с помощью: 1) выборочного коэффициента корреляции 2) частного коэффициента корреляции 3) множественного коэффициента корреляции 4) коэффициента корреляции по Спирмэну 5) квадратного коэффициента корреляции и углового критерия 6) коэффициента сопряженности 7) корреляционного отношения
Частные (парциальные) коэф. корреляции характеризуют тесноту связи между двумя случайными величинами системы при исключении влияния остальных случайных величин. Частный коэф. корреляции в-н Х1 и Х2, входящих в систему {Х1,Х2…Хn} относительно в-н Х3, Х4, …Хn обозначается через r12,34…n
![]()
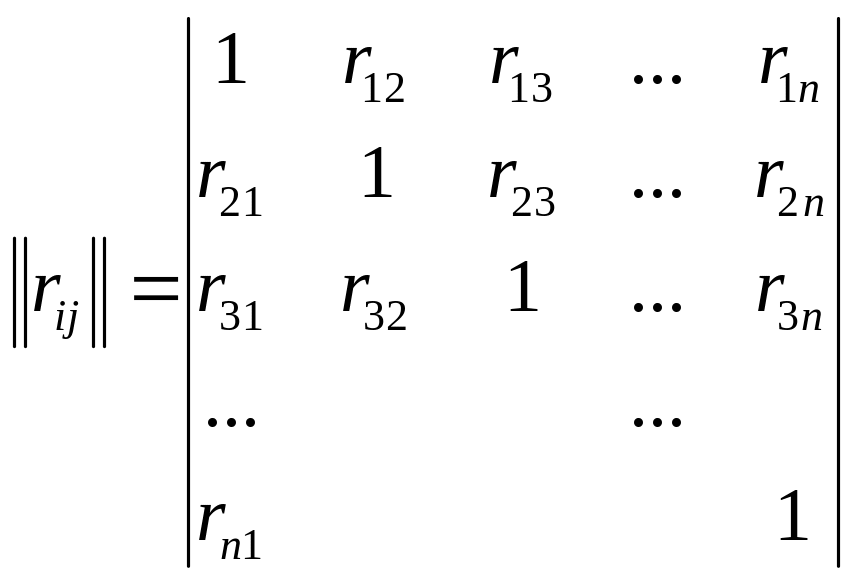 где
Р12-
минор детерминанта квадратной матрицы
(матрицы
коэф. корреляции), получаемой путем
вычеркивания 1ой
строки и 2го
столбца, умноженной на (-1)1+2=-1
где
Р12-
минор детерминанта квадратной матрицы
(матрицы
коэф. корреляции), получаемой путем
вычеркивания 1ой
строки и 2го
столбца, умноженной на (-1)1+2=-1
В отличие от коэф. множеств. корреляции коэф. частной корреляции как коэф. парной корреляции меняется в пределах от -1 до +1. Пи наличии корреляции частный коэф. корреляции r12,34…n в общем случае не равен коэф. парной корреляции r12.
Коэффициент множественной корреляции.
(сводный коэф. корреляции)
Используется
для описания системы сл. в-н {Х1,Х2…Хn}.
Служит характеристикой корреляции
между величиной Х1
с одной стороны и всей совокупностью
величин (Х2,Х3…Хn)
с другой.
![]() Р – детерминант квадратной матрицы
коэф. коррел.
Р – детерминант квадратной матрицы
коэф. коррел.
Р11 – минор этого детерминанта
При
n=3
 Свойства
1.
всегда является положительным числом
0≤r1(23..n)
≤1
2. при r1(23..n)=1
случайная величина Х1
почти наверное равна линейной комбинации
Х2,Х3…Хn.
3.
равенство r1(23..n)=0
имеет место тогда, когда r12,r13,…r1n=0,
т.е. случайная величина Х1
не коррелированна со всеми остальными
случайными величинами системы.
Свойства
1.
всегда является положительным числом
0≤r1(23..n)
≤1
2. при r1(23..n)=1
случайная величина Х1
почти наверное равна линейной комбинации
Х2,Х3…Хn.
3.
равенство r1(23..n)=0
имеет место тогда, когда r12,r13,…r1n=0,
т.е. случайная величина Х1
не коррелированна со всеми остальными
случайными величинами системы.
