
- •44. Фракталы, определение и примеры
- •43. Моделирование и подобие. Получение критериев подобия с помощью метода интегральных аналогов (пример с уравнением Навье-Стокса)
- •42. Моделирование и подобие; динамические аналогии; критерии подобия. Пи-теорема.
- •Компьютерные модели в автоматизированном управлении
- •40. Прямой метод Ляпунова
- •39. Подход к оценке устойчивости по линеаризованным уравнениям.
- •38. Определение устойчивости, устойчивость по Ляпунову
- •37. Инвариантность систем.
- •36. Управляемость и наблюдаемость
- •35.Представление в пространстве состояний и модель «вход-выход»
- •34. Единый подход к линеаризации.
- •33. Общая схема нечеткого вывода.
- •32. Нечеткое представление информации; типовые функции принадлежности, мера нечеткости.
- •31. Факторный анализ
- •30. Метод главных компонент
- •1.Среднее арифметическое переменных
- •7. Считаем дискриминантные функции
- •24. Непараметрическая статистика Манна-Уитни.
- •23. Составление статистических оценок ; анализ наиболее часто используемых законов распределения.
- •22. Составление статистической оценки на основе распределения Колмогорова – Смирнова.
- •21. Составление статистической оценки на основе распределения Фишера.
- •20. Составление статистических оценок ; анализ наиболее часто используемых законов распределения.
- •19. Общий подход к составлению статистических оценок
- •18. Проблема оценки адекватности моделей
- •17. Матричная форма мнк при построении модели (этап проверки адекватности полученной модели).
- •16. Матричная форма мнк при построении модели (этап проверки значимости коэффициентов модели).
- •15. Матричная форма мнк при построении модели (этап оценки коэффициентов модели).
- •13. Метод ранговой корреляции по Спирмэну.
- •12. Виды зависимостей. Корр анализ; коэффициенты частной и множественной корреляции.
- •11. Виды зависимостей. Корр анализ; коэфф парной корр-ии.
- •10.Метод наименьших квадратов - базовый метод получения коэффициентов регрессионных уравнений.
- •9.Виды зависимостей. Регрессионный анализ.
- •8. Классификация задач управления; задача оценивания.
- •Классификация задач управления; задача адаптивного управления
- •Классификация задач управления; задача детерминированного и стохастического управления.
- •Классификация задач управления. Задача идентификации.
- •3.Методология построения детерминированных моделей.
- •4.Основные виды зависимостей.
- •2. Общие подходы к построению моделей с учетом характера исходной информации.
- •Классификация моделей.
- •1. Дискретно - детерминированные модели
- •2. Непрерывно - детерминированные модели
- •3. Дискретно - стохастические модели
- •4. Непрерывно - стохастические модели
16. Матричная форма мнк при построении модели (этап проверки значимости коэффициентов модели).
МНК имеет три этапа: 1 этап Определение коэффициентов а. 2 этап Оценка достоверности коэффициентов а. 3 этап Проверка адекватности модели.
Ошибка
оценивания.
Реально
![]() отличается от
отличается от
![]() .
Дисперсия - мера отличия. Чем больше
дисперсия, тем больше отличие. Дисперсия
будет зависеть как от дисперсии ошибок
наблюдения σ2,
так и от точек постановки опытов.
.
Дисперсия - мера отличия. Чем больше
дисперсия, тем больше отличие. Дисперсия
будет зависеть как от дисперсии ошибок
наблюдения σ2,
так и от точек постановки опытов.
![]()
![]() -
ковариационная матрица.
-
ковариационная матрица.
![]() Поставим вместо а ее оценку и с учетом
условий запишем все необходимые
выражения.
Поставим вместо а ее оценку и с учетом
условий запишем все необходимые
выражения.
![]() Так
как корреляционная матрица симметрична,
то при
Так
как корреляционная матрица симметрична,
то при
![]() - дисперсия коэффициента аi
- дисперсия коэффициента аi
![]() Действует нормальный закон распределения.
Действует нормальный закон распределения.
![]() -
стандартное отклонение
-
стандартное отклонение
![]() , где Ф(ε)
– функция Лапласа
α→Р→ε
α
– уровень значимости
(0,1;0,05;0,01)
1-α=Р
Р-вероятность,ε
–
из таблицы интегралов
Пусть
Р=0,95, следовательно ε=1,96
, где Ф(ε)
– функция Лапласа
α→Р→ε
α
– уровень значимости
(0,1;0,05;0,01)
1-α=Р
Р-вероятность,ε
–
из таблицы интегралов
Пусть
Р=0,95, следовательно ε=1,96
![]() ,
где σ2-
дисперсия ошибки наблюдения.
Если
σ2
задана, то
,
где σ2-
дисперсия ошибки наблюдения.
Если
σ2
задана, то
![]() Если
Если
![]() , то Н0
имеет место (не отвергается)
, то Н0
имеет место (не отвергается)
15. Матричная форма мнк при построении модели (этап оценки коэффициентов модели).
МНК
имеет три этапа:
= (a0...ak)
- вектор- столбец
x
= (x1...xk)
- вектор- столбец
f(x)
= (1, x1,..,
xk)
![]() - наблюдаемые значения,
– оценки,
- истинные значения
- наблюдаемые значения,
– оценки,
- истинные значения
![]() Эксперимент проводится в N
точках, т.о. фиксируем x
и
y.
x1,
x2,...,
xN
- точки экспериментов.
xi
= (xi1,
xi2,...,
xin) 1
i
N
Эксперимент проводится в N
точках, т.о. фиксируем x
и
y.
x1,
x2,...,
xN
- точки экспериментов.
xi
= (xi1,
xi2,...,
xin) 1
i
N
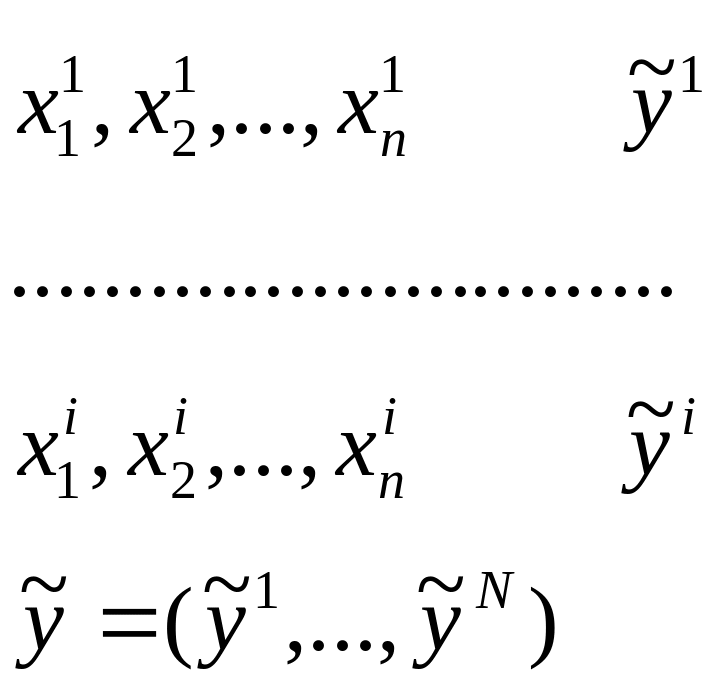 -
вектор наблюдений функции отклика.
-
вектор наблюдений функции отклика.
Для оценки адекватности модели в любой точке xi эксперимент повторяется раз.
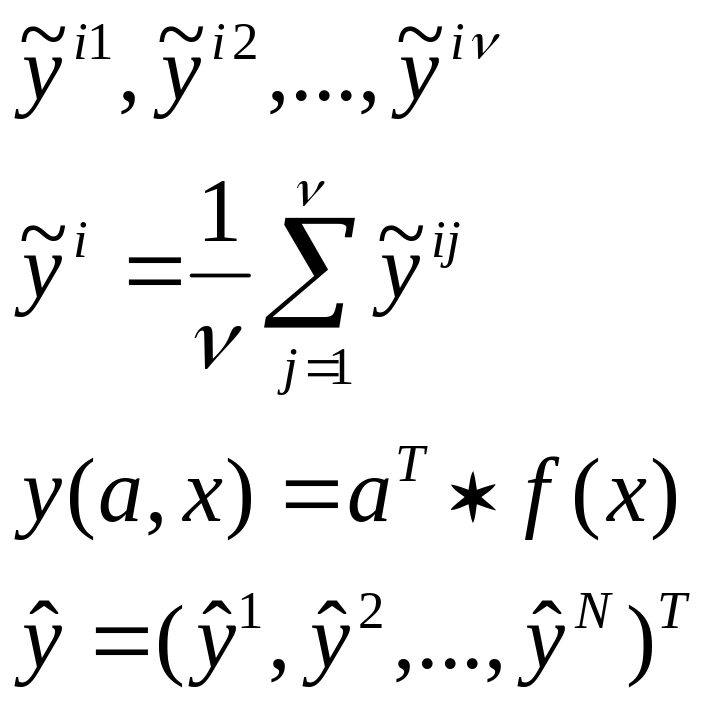
Информационная матрица
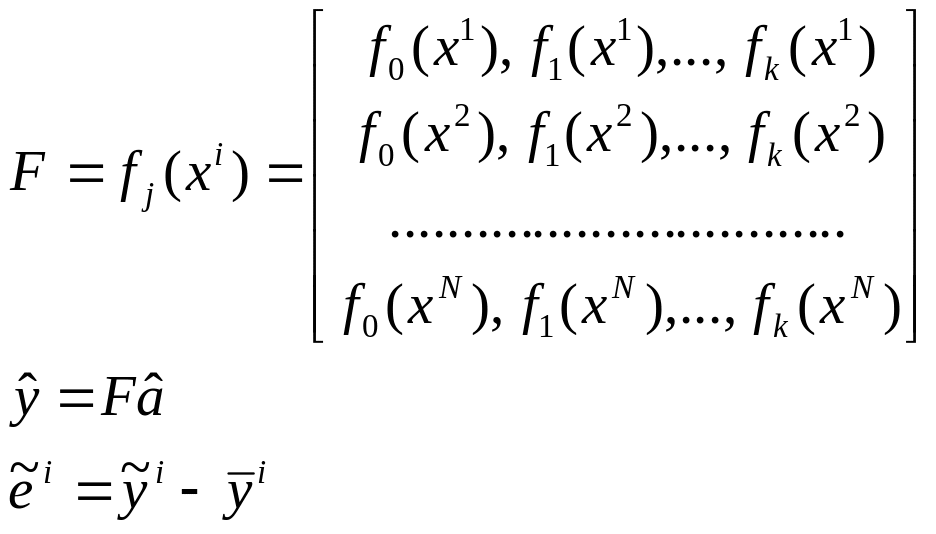
- ошибка, погрешность.
Требуемые
условия.
1.
Результаты наблюдений свободны от
систематических ошибок
![]() E
- математическое ожидание.
2.
Результат наблюдений в точке xj
не зависит от результата наблюдений в
точке xi
.
E
- математическое ожидание.
2.
Результат наблюдений в точке xj
не зависит от результата наблюдений в
точке xi
.
![]() 3.
Дисперсия результатов наблюдений во
всех точках одинакова.
3.
Дисперсия результатов наблюдений во
всех точках одинакова.
![]() для
любых i.
4.
Оценка
является несмещенной
для
любых i.
4.
Оценка
является несмещенной
![]() 5.
Дисперсия оценки
5.
Дисперсия оценки
![]() должна
быть минимальна
должна
быть минимальна
 где
- оценка, которая еще пока не найдена.
где
- оценка, которая еще пока не найдена.
![]()
Так
как S/a
= 0 то
![]() следовательно
следовательно
![]()
x
 i
i
14.
Корреляционное отношение
Применение коэф. корреляции ограничивается
случаем линейной связи. Для оценки
нелинейной связи используют корреляционное
отношение. Корреляционное отношение
требует расчета условных дисперсий.
Зависимость
Dу׀х
=
φ(х)
–
скедастическая
функция. Если φ(х)=const,
то условная дисперсия переменной У
–постоянна, не зависит от х и говорят,
что связь между случайными переменными
у и х гомоскедастическая.
Чтобы получить представление о рассеянии
случайной переменной у во всем диапазоне
изменения переменной Х1
используют вероятностную, называемую
средней условной дисперсией
![]() . По гомоскедастической связи, когда
Dу׀х
=const,
то
ничем не отличается от Dу׀х
.
По
определению
. По гомоскедастической связи, когда
Dу׀х
=const,
то
ничем не отличается от Dу׀х
.
По
определению
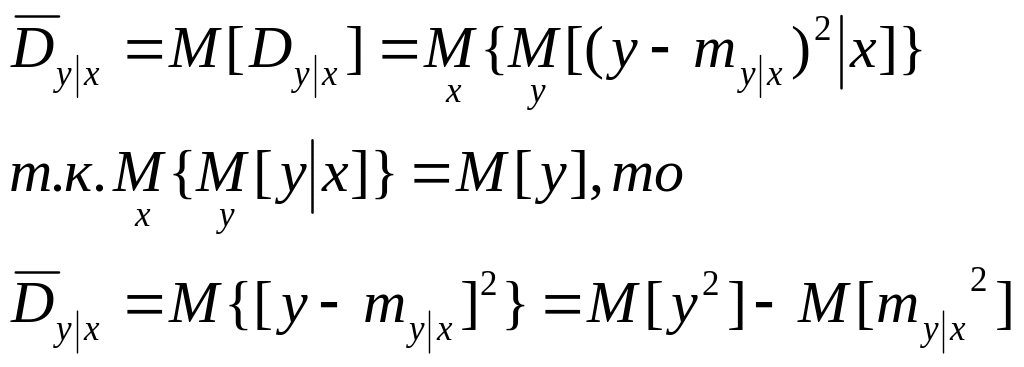 Установим
соотношение между полной дисперсией
Dy
и средней условной дисперсией
. Формула полной дисперсии случайной
переменной у записывается в виде
Dy=
M[
y2
]-m2y,
my=
M[y]
Cделаем
искусственное преобразование. Прибавим
и отнимем от правой части M[m2ylx],
где mylx=
M[y
l
x]
-условное мат.ожидание
Dy=
M[
y2
]
- M[m2ylx]
+ M[m2ylx]
- m2y
Вспомним,
что
= M[
y2
] - M[
m2ylx]
M[m2ylx]
- m2y
= D{M[ylx]}
Это
следует из D{M[ylx]}
= D[mylx]
= M[m2ylx]
- {M[mylx]}2
=
M[m2ylx]-m2y,
т.е.
Dy=
+ D{M[ylx]}
Это
формула разбиения дисперсий.
Установим
соотношение между полной дисперсией
Dy
и средней условной дисперсией
. Формула полной дисперсии случайной
переменной у записывается в виде
Dy=
M[
y2
]-m2y,
my=
M[y]
Cделаем
искусственное преобразование. Прибавим
и отнимем от правой части M[m2ylx],
где mylx=
M[y
l
x]
-условное мат.ожидание
Dy=
M[
y2
]
- M[m2ylx]
+ M[m2ylx]
- m2y
Вспомним,
что
= M[
y2
] - M[
m2ylx]
M[m2ylx]
- m2y
= D{M[ylx]}
Это
следует из D{M[ylx]}
= D[mylx]
= M[m2ylx]
- {M[mylx]}2
=
M[m2ylx]-m2y,
т.е.
Dy=
+ D{M[ylx]}
Это
формула разбиения дисперсий.
Т.е. полная дисперсия является суммой средней условной дисперсии и дисперсии условного математического ожидания. Поясним это. Если х – входная, а у – выходная переменные, то дисперсия условного мат. ожидания D{M[ylx]} представляет собой ту часть полной дисперсии Dy выходной переменной у, которая связана с влиянием входной переменной х. Вторая часть полной дисперсии – средняя условная дисперсия – определяется влиянием совокупности всех остальных переменных, кроме учтенной переменной х. Так как = Dy – D{M[ylx]} , то ≤Dy Равенство имеет место, когда D{M[ylx]} = 0 В качестве меры корреляц. отношения принято η2yx=1 - / Dy ; ηyx – корреляц. отношение
Свойства: 1. 0 ≤ ηyx ≤ 1 ; 0 ≤ ηxy ≤1. Это свойство следует из формул ηyx=1- /Dy ηxy = 1- /Dx
аналогично η2yx= D{ M[ylx] } / Dy η2xy = D{ М[xly] } / Dx 2. Величина η всегда положительна. 3. Равенство ηyx= 0 означает, что переменная y не коррелированна с переменной x. Если x и y – независимы, то ηyx= 0. 4. Равенство ηyx=1 соответствует функциональной связи между y и x. 5. В общем случае ηyx ≠ ηxy, т.е. данная связь несимметрична
6. Если связь между переменными x и y линейна, то ηyx= ηxy. 7. При линейной регресии ηyx= ׀ryx ׀, т.е. корреляционное отношение служит характеристикой и линейной связи. 8. При нелинейной регрессии всегда ηyx> ׀ryx ׀, т.е. коэффициент корреляции при нелинейной стохастической связи дает заниженные оценки. Разность η2yx-r2yx=h2yx – индикатор степени нелинейности стохастической связи.
