
- •44. Фракталы, определение и примеры
- •43. Моделирование и подобие. Получение критериев подобия с помощью метода интегральных аналогов (пример с уравнением Навье-Стокса)
- •42. Моделирование и подобие; динамические аналогии; критерии подобия. Пи-теорема.
- •Компьютерные модели в автоматизированном управлении
- •40. Прямой метод Ляпунова
- •39. Подход к оценке устойчивости по линеаризованным уравнениям.
- •38. Определение устойчивости, устойчивость по Ляпунову
- •37. Инвариантность систем.
- •36. Управляемость и наблюдаемость
- •35.Представление в пространстве состояний и модель «вход-выход»
- •34. Единый подход к линеаризации.
- •33. Общая схема нечеткого вывода.
- •32. Нечеткое представление информации; типовые функции принадлежности, мера нечеткости.
- •31. Факторный анализ
- •30. Метод главных компонент
- •1.Среднее арифметическое переменных
- •7. Считаем дискриминантные функции
- •24. Непараметрическая статистика Манна-Уитни.
- •23. Составление статистических оценок ; анализ наиболее часто используемых законов распределения.
- •22. Составление статистической оценки на основе распределения Колмогорова – Смирнова.
- •21. Составление статистической оценки на основе распределения Фишера.
- •20. Составление статистических оценок ; анализ наиболее часто используемых законов распределения.
- •19. Общий подход к составлению статистических оценок
- •18. Проблема оценки адекватности моделей
- •17. Матричная форма мнк при построении модели (этап проверки адекватности полученной модели).
- •16. Матричная форма мнк при построении модели (этап проверки значимости коэффициентов модели).
- •15. Матричная форма мнк при построении модели (этап оценки коэффициентов модели).
- •13. Метод ранговой корреляции по Спирмэну.
- •12. Виды зависимостей. Корр анализ; коэффициенты частной и множественной корреляции.
- •11. Виды зависимостей. Корр анализ; коэфф парной корр-ии.
- •10.Метод наименьших квадратов - базовый метод получения коэффициентов регрессионных уравнений.
- •9.Виды зависимостей. Регрессионный анализ.
- •8. Классификация задач управления; задача оценивания.
- •Классификация задач управления; задача адаптивного управления
- •Классификация задач управления; задача детерминированного и стохастического управления.
- •Классификация задач управления. Задача идентификации.
- •3.Методология построения детерминированных моделей.
- •4.Основные виды зависимостей.
- •2. Общие подходы к построению моделей с учетом характера исходной информации.
- •Классификация моделей.
- •1. Дискретно - детерминированные модели
- •2. Непрерывно - детерминированные модели
- •3. Дискретно - стохастические модели
- •4. Непрерывно - стохастические модели
18. Проблема оценки адекватности моделей
Имитационное моделирование имеет особые трудности при решении проблемы адекватности модели, т.к. велик информационный фонд и сама модель – это совокупность большого количества моделей.
- методы внешней оценки (эксперт оценивает входы, выходы, структуру, примерные результаты);
- трассировка (анализируется логика моделирования);
- внутренняя оценка (статистические критерии, типа критерия Фишера);
исторические подходы.
Статистические критерии- проблем нет!
Р аспределение
Фишера.
F-
статистика Фишера;
аспределение
Фишера.
F-
статистика Фишера;
F- критерий или критерий Фишера. fF F
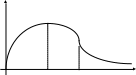
Пусть S12 и S22 - дисперсии независимых случайных выборок объемом n1 и n2. Тогда случайная величина F, равная F = S12 / S22 подчиняется распределению Фишера с параметрами 1 и 2 (при S12 > S22) 1 = n1 – 1 ; 2 = n2 - 1 F-распределение - непрерывная асимметричная функция, определенная на интервале [0, +]. Fкр находим на основе , 1, 2.
Расстояние
Махаланобиса
dM
(Xi
, Xj) =
(Xi
- Xj)т
W
-1
(Xi
- Xj),
где W
-1 - матрица, обратная к матрице рассеяния
dM
(Xi
, Xj) =
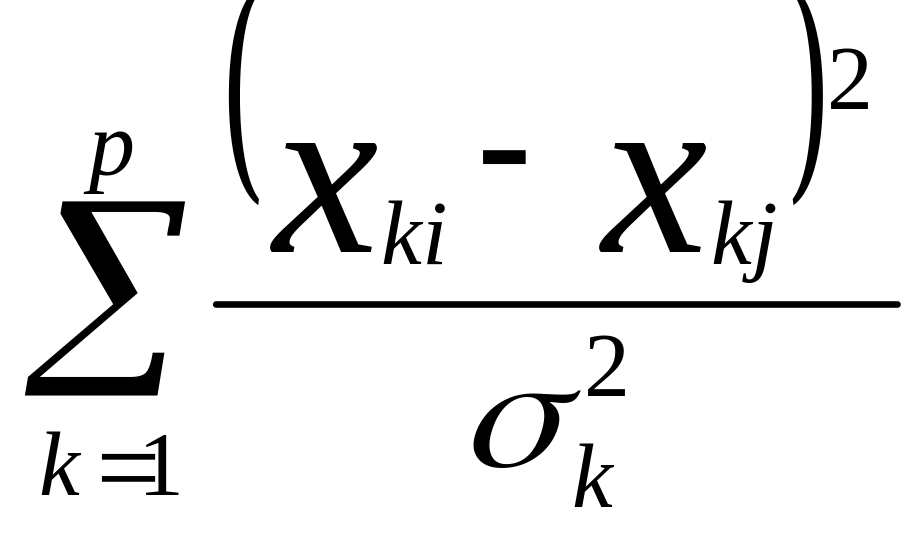
1.Максимальное расхождение между эмпирической и теоретической кривой(Критерий согласия Колмогорова- Смирного)
Алгоритм применения критерия.
Расчет эмпирических кривых распределения: F1n(x), F2n(z).
1-ая выборка х1, х2,…,хn,
2-ая выборка z1, z2,…,zm;
Для этого упорядочим в порядке возрастания каждую последовательность x и z, построим кумулятивную функцию распределения.
Определение верхнего предела (или верхней грани) – Dn,m - модуля эмпирических распределений.
Определение при заданном уровне значимости табличного значения Dα. (Dα – рассчитывается по сложной формуле).
Сравнение значений Dn,m и Dα .Если Dn,m < Dα , то гипотеза о торжественности двух выборок не отвергается.
2. МНК
3. Теория регулирования
17. Матричная форма мнк при построении модели (этап проверки адекватности полученной модели).
Виды
регрессий.
1.
Линейный
одномерный случай
y
= a0
+ a1x
2.
Параболическая
или степенная регрессия
![]()
3 .
Линейная
множественная регрессия
.
Линейная
множественная регрессия
![]() x1,...,xn
y
x1,...,xn
y
 факторы функция
отклика
y(a,x)
= a0
+ a1x1
+...+ anxn
+ an+1x12
+...+ a2nxn2
+ a2n+1x1x2
+...+ akxn-1xn
k+1
= (n+1)(n+2)/2
- число неизвестных
факторы функция
отклика
y(a,x)
= a0
+ a1x1
+...+ anxn
+ an+1x12
+...+ a2nxn2
+ a2n+1x1x2
+...+ akxn-1xn
k+1
= (n+1)(n+2)/2
- число неизвестных
![]() = ?.
= ?.
МНК имеет три этапа: 1 этап Определение коэффициентов а. 2 этап Оценка достоверности коэффициентов а. 3 этап Проверка адекватности модели.
П роверка
адекватности модели.
Н0:
tр
tкр
где tр
- расчетное значение ; tкр
- табличное значение
1- a
= р
роверка
адекватности модели.
Н0:
tр
tкр
где tр
- расчетное значение ; tкр
- табличное значение
1- a
= р
a В основе проверки адекватности модели лежит сопоставление достигнутой точности модели с точностью наблюдения. Для оценки точности используем дисперсию, поэтому необходимо сравнить дисперсию ошибки по модели с дисперсией ошибки наблюдений. Поэтому в каждой точке эксперимент повторяется раз.
![]() отсюда
следует, что
отсюда
следует, что
![]()
1.Дисперсия
ошибки моделирования.
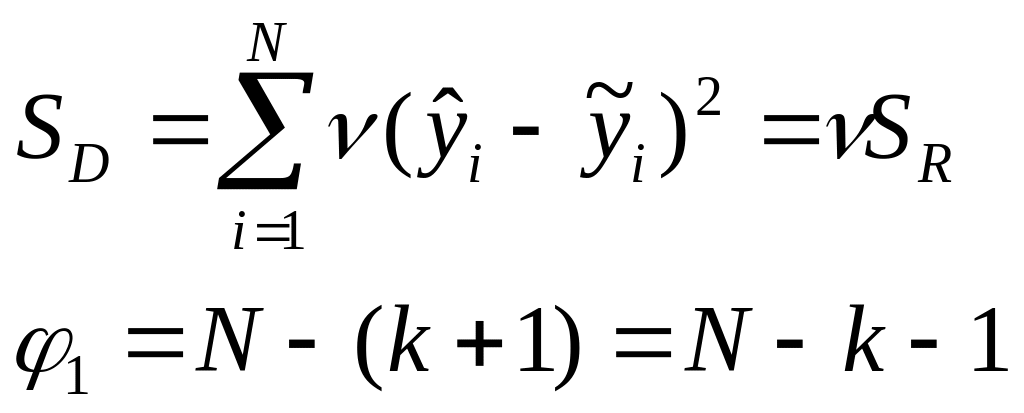
2.
Дисперсия
ошибки наблюдения
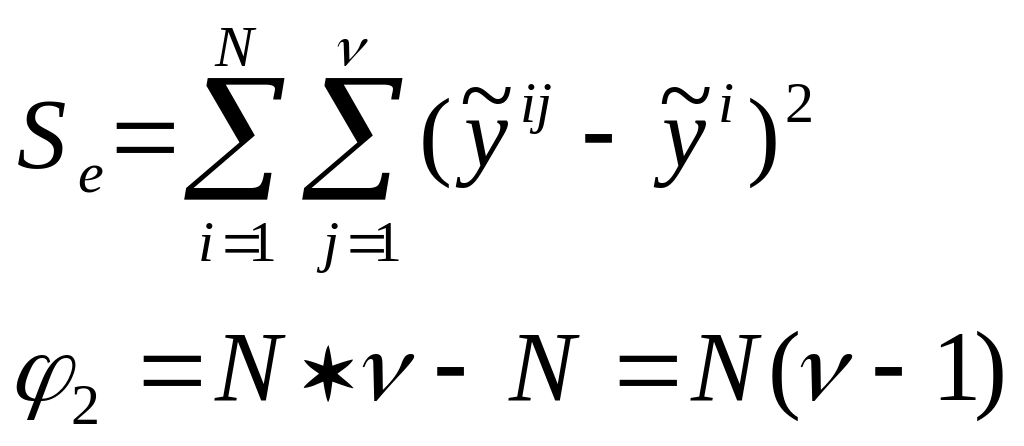
 Далее
рассчитываем статистику Фишера Fр
= (SD/1)/(Se/2).
Если ошибка моделирования меньше ошибки
наблюдения, то модель хорошая. Выдвигается
гипотеза Н0.
Определяется уровень значимости .
В
соответствии с ,
1
и 2
из таблицы находим Fкр.
P{F
< Fкр}
= 1-
fF
F
Fp
Fкр
Если
Fp
Fкр,
то модель адекватна.
Далее
рассчитываем статистику Фишера Fр
= (SD/1)/(Se/2).
Если ошибка моделирования меньше ошибки
наблюдения, то модель хорошая. Выдвигается
гипотеза Н0.
Определяется уровень значимости .
В
соответствии с ,
1
и 2
из таблицы находим Fкр.
P{F
< Fкр}
= 1-
fF
F
Fp
Fкр
Если
Fp
Fкр,
то модель адекватна.
