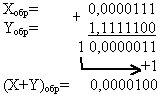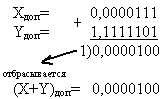3. Машинные коды

2.3.1 Краткая теория вопроса

В вычислительных устройствах операции вычитания, деления, умножения сводятся к операциям сложения и сдвига промежуточных материалов влево или вправо в зависимости от выполняемого действия. Это становится возможным, если в операциях участвуют не сами числа, а их коды. Существуют три вида кодов: прямой, обратный и дополнительный.

При представлении положительных чисел в форме с фиксированной точкой прямой, обратный и дополнительный коды совпадают по изображению. В знаковой части «плюс» кодируется нулем.

Пример: представим число А в прямом, обратном и дополнительном коде в восьмиразрядной сетке.

А = +1001₂

А_пр=А_обр=А_доп=0.0001001

Коды отрицательных чисел не совпадают по изображению. Последовательность и правила кодирования отрицательного числа А = -1010₂, представленного в формате восьмиразрядной сетки, показаны в таблице.

Таблица 2 – Кодирование отрицательного числа

Название кода	Правила кодирования	Вид закодированного числа
Прямой	Изображение кода совпадает с изображением числа. В знаковой части «минус» кодируется единицей	Апр = 1.0001010
Обратный	Обратный код получается из прямого по следующему правилу: значение каждого разряда после точки меняется на обратное – 1 на 0, 0 на 1. Код знака остается без изменений	Аобр = 1.1110101
Дополнительный	Образуется как обратный код с добавлением 1 к младшему разряду	1.1110101 + 1 Адоп = 1.1110110

Правило перевода из обратного/дополнительного кода в прямой код аналогично правилу перевода из прямого кода в обратный/дополнительный.

Примеры

Аобр = 1.1110101 Апр = 1.0001010

Адоп = 1.1110110 Апр = 1.0001001 + 1 1.0001010

Правило сложения чисел с разными знаками в обратных кодах: производится поразрядное сложение чисел, начиная с младшего разряда и включая знаковый разряд. Если образуется единица переноса из знакового разряда, то его добавляют к младшему разряду суммы.	Пример
Правило сложения чисел с разными знаками в дополнительном коде: аналогично сложению в обратных кодах, но единица переноса из знакового разряда отбрасывается.	Пример

2.3.2 Тексты заданий по индивидуальным вариантам

Содержание заданий со ссылкой на таблицу и оценкой за правильное выполнение в баллах приведено ниже:

10) Представить десятичное число со знаком в машинном коде в восьмиразрядной сетке (таблица 5, максимум 5 баллов).

11) Задан 16-ричный машинный код числа со знаком (8-разрядная сетка), определить десятичное значение данного числа (таблица 5, максимум 5 баллов).

12) Даны числа А и В, найти А – В, В – А в двоичных машинных кодах в 8 разрядной сетке, в заданном коде, результат записать в десятичной системе счисления (таблица 5, максимум 20 баллов).