Министерство топлива и энергетики Украины
Севастопольский национальный университет ядерной энергии и промышленности
УТВЕРЖДАЮ:
Заведующий кафедрой ПФНФ
И.И. Марончук
____________________________
«___» __________ 2011 г.
Кафедра прикладной физики и нанофизики
Обработка измерений
Методические указания для студентов всех специальностей
Разработчик:
Доцент кафедры ПФНФ А.Г. Рипп
__________________ « _____» ___________2011 г.
Севастополь
2011
Введение
При выполнении лабораторных работ по физике не достаточно просто провести измерения каких-то величин – важно ещё правильно обработать полученные результаты. В эту обработку входят разные элементы, из которых основными являются следующие.
Оценка погрешностей измерений.
Построение графиков.
Формулировка выводов.
В данном пособии предлагаются рекомендации, как выполнять эти элементы.
Оценка погрешностей измерений
При любом измерении ошибка неизбежна. Эту ошибку называют погрешностью измерения. Величина погрешности зависит, в основном, от трёх факторов: от качества применяемых приборов, от аккуратности экспериментатора и от методики измерения. Точное значение погрешности всегда неизвестно, иначе можно было бы её учесть и, следовательно, устранить. Однако погрешность можно оценить, то есть выяснить, в каких разрядах числа, полученного при измерении, может содержаться ошибка. Например, результат измерения силы тока – пятизначное число 21,356 мА. За какие из этих пяти цифр можно быть на 100% уверенным? Если только за первые две цифры, значит, погрешность составляет десятые доли мА, а если экспериментатор уверен и в десятых долях мА, но сомневается в сотых, то погрешность составляет сотые доли мА. Вот в этом и состоит оценка погрешности – выяснение того, на сколько примерно мог ошибиться экспериментатор при проведении измерения.
Абсолютная и относительная погрешности
Пусть X – некоторая физическая величина, x – результат её измерения, х – истинное значение. Так как не существуют идеальные измерительные приборы и человек, проводящий измерения, тоже далёк от совершенства, то ясно, что x x. Повторное измерение величины X, произведённое в тех же условиях и с помощью тех же измерительных приборов, даст другое значение x, которое тоже не равно истинному значению x.
Область значений, в которой лежат возможные результаты измерения величины X для данной методики измерений и при данных измерительных приборах, называется доверительным интервалом величины X.
Д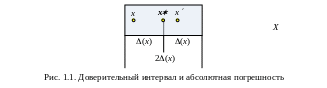
оверительный
интервал изображён на рисунке 1.1.
Чем меньше ширина доверительного интервала 2(x), тем точнее можно измерить величину X, тем меньше погрешность.
Абсолютной погрешностью (x) измерения величины X называется полуширина доверительного интервала.
Относительной погрешностью измерения величины X называется отношение абсолютной погрешности (x) к результату измерения x. Относительная погрешность обозначается буквами (x) или (x).
. (1.1)
Часто относительную погрешность измеряют в процентах. Тогда формулу (1.1) пишут в виде:
. (1.2)
Приборная и случайная погрешности
Погрешность измерения величины X можно разделить на сумму двух составляющих – приборную погрешность п(x) и случайную с(x):
. (1.3)
Приборная погрешность определяется классом точности приборов, применяемых для измерения X, случайная погрешность определяется действием случайных факторов – неточностью действий человека, производящего измерения, и колебаний параметров среды, в том числе параметров измерительной установки (давления, температуры, освещённости, напряжения в сети и т.д.).
Оценка приборной погрешности зависит от того, к какому из двух классов относится способ измерения величины X. Первый класс – это прямые измерения, второй класс – косвенные измерения.