2.2. Задание и примеры решения задач по первой части ргр

На рисунках 2.9 и 2.10 приведены два варианта схем трехфазных цепей. В каждой из них имеется трехфазный генератор (на рисунках 2.9, 2.10 не показан), создающий трехфазную симметричную синусоидальную систему ЭДС частотой 50 Гц, трехфазная линия электрической связи и трехфазная нагрузка. Действующие значения линейного напряжения, параметры, определяющие сопротивления линии и фаз нагрузки схем (рисунок 2.9 и рисунок 2.10), приведены в таблице А.1 (см. приложение А).

Требуется для схем, рис.2.9, 2.10:

1. Рассчитать токи и напряжения на всех элементах трехфазной цепи.

2. Проверить баланс активных и реактивных мощностей.

3. Включить в схему ваттметры для измерения мощности трехфазной цепи и определить их показания.

4. Построить векторную топографическую диаграмму.

Вариант 1.

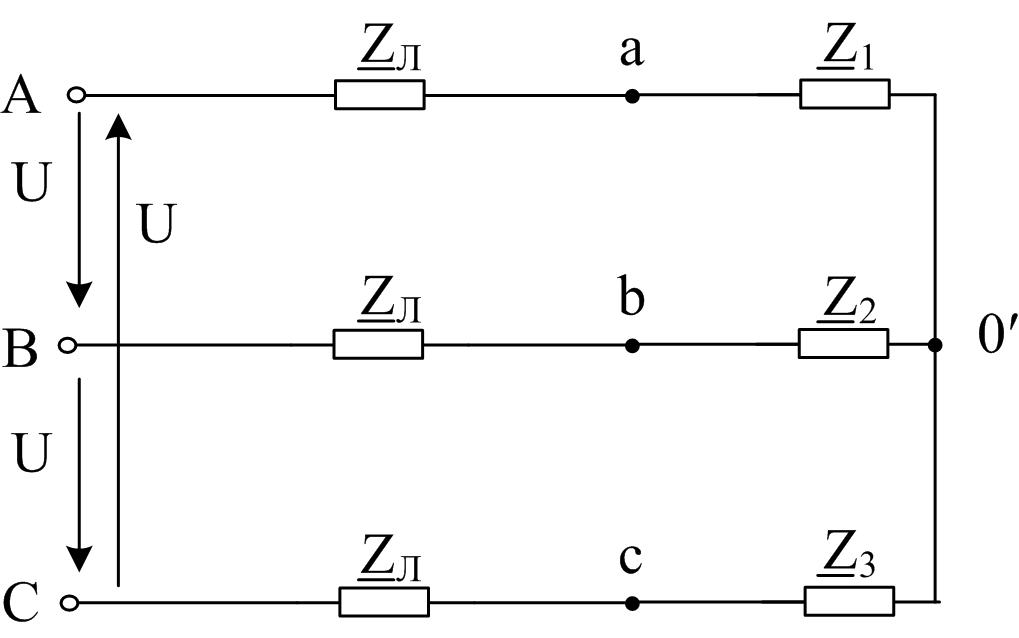
Рисунок 2.9

16

Таблица Б.4 –

UMaв, A	0	100	150	200	250	300	350
H2ℓ2, A	300	200	150	100	50	0	-50
H2, A/м	1200	800	600	400	200	0	-200
B2, Тл	1,33	1,18	1,08	0,91	0,59	0	-0,59
Φ2, 10-3Вб	3,19	2,83	2,59	2,18	1,42	0	-1,42

Таблица Б.5 –

UMaв, A	0	100	150	200	250	300	350
Φ1+Φ2,10-3Вб	6,502	5,880	5,422	4,772	3,604	1,416	-1,42

Далее определим зависимость магнитного потока Φ₃ среднего стержня от магнитного напряжения U_мaв. Для этого зададимся магнитными потоками Φ₃, ориентировочные значения которых примем с учетом данных таблицы Б.5, последовательно вычислим (по кривой намагничивания), . Данные расчетов сведены в таблицу Б.6.

Таблица Б.6 –

Φ3, 10-3Вб	0	1,0	2,0	3,0	4,0	5,0
B3, Тл	0	0,28	0,56	0,84	1,12	1,4
H3, A/м	0	115	190	365	660	1580
H4, A/м	0	224∙103	448∙103	672∙103	896∙103	1120∙103
H3ℓ3, A	0	13,8	22,8	43,8	79,2	189,6
Hδδ, A	0	33,6	67,2	100,8	134,4	168,0
Uмab, A	0	47,4	90,0	144,6	213,6	357,6

По данным таблиц (Б.3)–(Б.6) в одних и тех же координатах построим магнитные характеристики , , , .

81

Дальнейшее решение сводится к графическому построению магнитных характеристик с учетом уравнений, составленных по законам Кирхгофа. Такое построение можно выполнить, например, по методу двух узлов, если ввести в рассмотрение магнитное напряжение между узлами а и b по стержню 3 (без обмотки):

. (Б.2)

Тогда из уравнений (Б.1), (Б.2) для этого магнитного напряжения равенства, связывающие с напряженностью поля в стержнях 1 и 2:

, откуда ;

, откуда .

Далее произведем вычисления зависимости магнитного потока Φ₁ от магнитного напряжения U_мав. Задаваясь магнитным напряжением U_мaв в пределах от 0 до F₁=350 A, определим величины H₁ℓ₁, H₁, B₁ (по кривой намагничивания, рисунок Б.2 – кривая 2), Φ₁= B₁S₁. Расчетные данные сводим в таблицу Б.3. (Отметим здесь, что можно задаваться значениями потока Φ₁, находить B₁, H₁, U_мaв).

Таблица Б.3 –

Uмaв, A	0	100	150	200	250	300	350
H1ℓ1, A	350	250	200	150	100	50	0
H1, A/м	1400	1000	800	600	400	200	0
B1, Тл	1,38*	1,27	1,18	1,08	0,91	0,59	0
Φ1, 10-3Вб	3,312	3,048	2,832	2,592	2,184	1,416	0

* – B₁=1,38 получено по экстраполяции кривой 2 (рисунок Б.2) до H₁=1400.

Аналогично определим зависимость Φ₂ от U_мaв. Для этого найдем H₂ℓ₂, H₂, B₂ и Φ₂= B₂S₂. Данные расчета сведем в таблицу Б.4.

Кривую построим по данным таблицы Б.3 и Б.4, результаты расчетов сведем в таблицу Б.5.

80

Вариант 2.

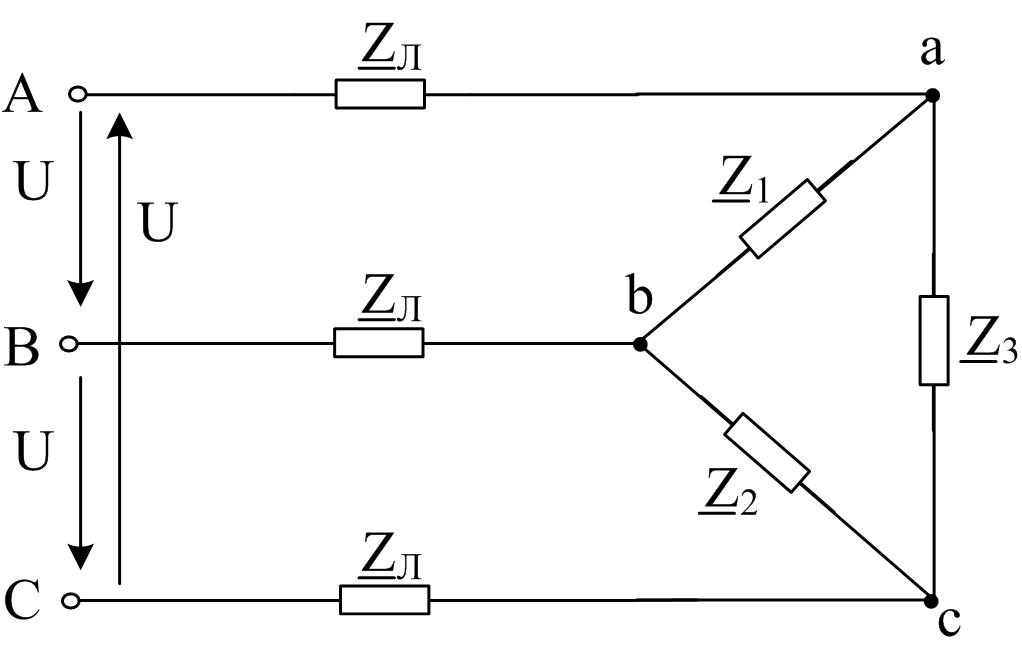
Рисунок 2.10

Приведем примеры расчета схем рис. 2.9 и рис. 2.10 по следующим данным:

Ом; мГн; Ом;

мкФ; мГн; Ом; мкФ.

2.2.1. Соединение нагрузки звездой

Согласно заданным параметрам нарисуем схему трехфазной цепи при соединении нагрузки звездой (рисунок 2.11).

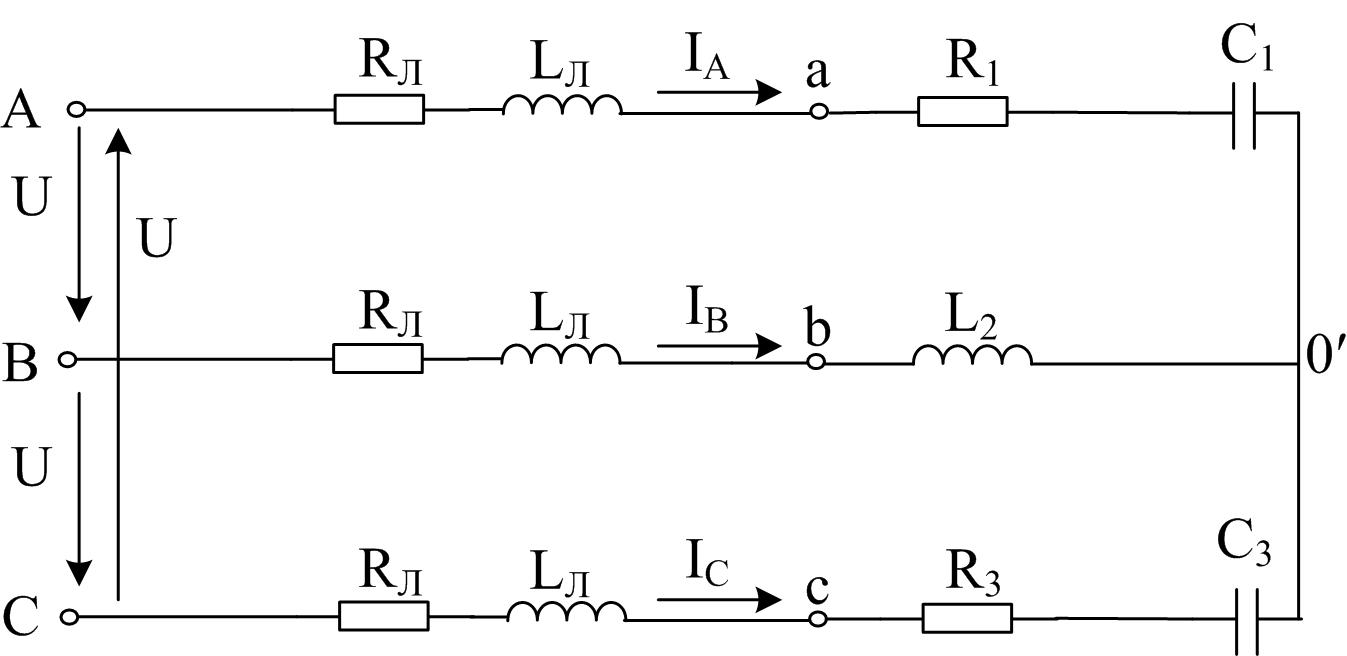
Рисунок 2.11

Решение. Определим сопротивления и проводимости данной цепи:

где

.

17

Сопротивление линии:

Ом.

Сопротивление фаз нагрузки:

Сопротивления линии и нагрузки соединены последовательно, т.е.:

Проводимости фаз:

Так как трехфазный источник симметричный, то комплексы его фазных напряжений равны:

18

Сечение воздушного зазора определим, пренебрегая «выпучиванием» силовых линий поля, т.е. примем его равным сечению третьей ветви:

.

Составим уравнения на основании законов Кирхгофа для магнитной цепи. Для данной магнитной цепи система должна содержать три независимых уравнения, одно из которых составляется по первому закону Кирхгофа, а два других – по второму закону Кирхгофа. Для удобства составления этих уравнений можно изобразить схему замещения рассматриваемой магнитной цепи по аналогии с электрическими цепями (рисунок В.8).

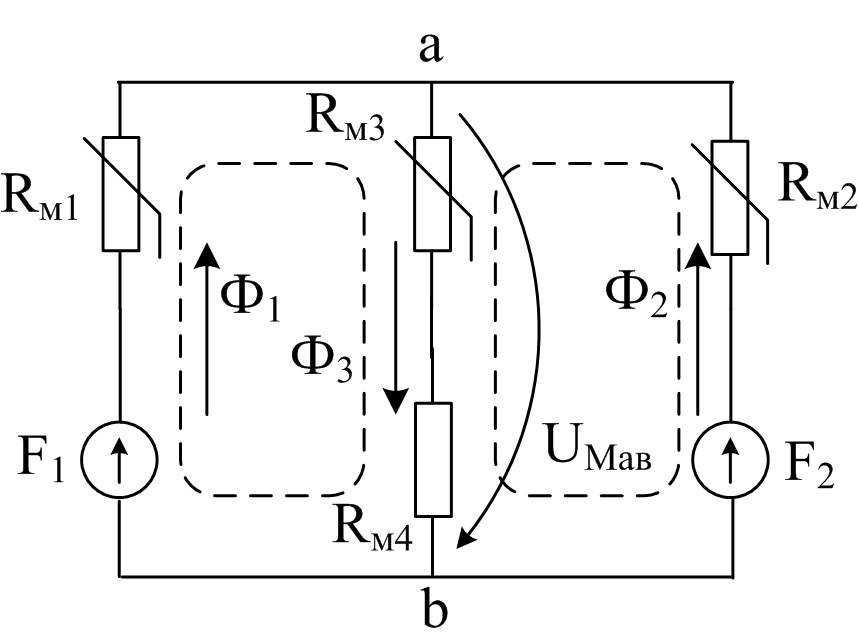
Рисунок В.8

С учетом выбранных положительных направлений магнитных потоков и обходов контуров можно записать:

,

или иначе

;

(Б.1)

Определим МДС обмоток:

Магнитная цепь несимметрична из-за того, что Н₁ ≠ Н₂.

79

Определить магнитные потоки в магнитной цепи, если в первой обмотке проходит ток I₁ = 3,5 A, а во второй обмотке I₂ = 1,5 A.

Решение. Это обратная задача расчета разветвленной магнитной цепи, решим ее по методу двух узлов.

На эскизе магнитной цепи изобразим среднюю силовую линию магнитного поля, укажем выбранные положительные направления магнитных потоков, выделим однородные участки и определим их геометрические размеры (рисунок Б.7).

Данная магнитная цепь содержит два узла и три ветви, поэтому в ней могут создаваться три различных магнитных потока Φ₁, Φ₂, Φ₃. В этой магнитной цепи можно рассматривать четыре однородных участка: три из них ℓ₁, ℓ₂, представляют собой электротехническую сталь, а четвертый – воздушный зазор δ.

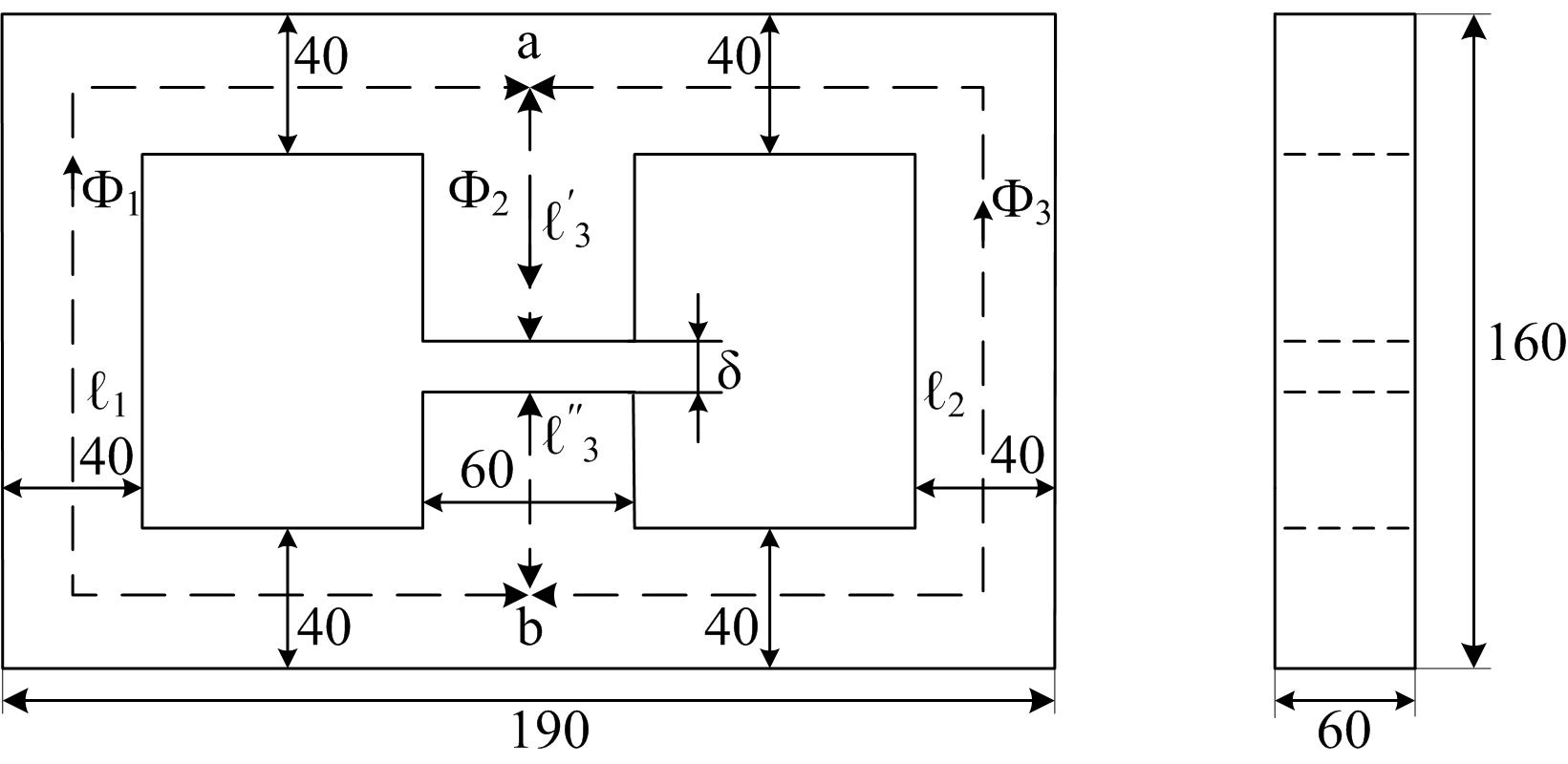
Рисунок Б.7

Длины однородных участков ℓ₁ и ℓ₂ определим, пренебрегая скруглениями силовых линий поля в углах магнитопровода:

Длину однородного участка ℓ₃ вычислим, пренебрегая величиной воздушного зазора:

Сечения ветвей магнитопровода найдем, считая коэффициент заполнения стали равным единице:

.

78

Так как комплексные сопротивления и не равны между собой, то данная трехфазная цепь – не симметрична, следовательно, необходимо определить напряжение смещения нейтрали:

Определим фазные напряжения потребителя:

По закону Ома определяем токи:

Проверка токов по первому закону Кирхгофа:

.

Рассчитываем напряжения на элементах трехфазной цепи (рис. 2.11).

Падения напряжения в линии:

19

Падения напряжения на фазах нагрузки:

Проверим баланс активных и реактивных мощностей.

Комплекс полной мощности, вырабатываемой источником энергии:

Потребляемая мощность:

.

Баланс активных мощностей:

.

Баланс реактивных мощностей:

Таким образом, баланс активных и реактивных мощностей соблюдается, что подтверждает правильность расчетов.

Определим активную мощность методом двух ваттметров. Включим ваттметры, как показано на рисунке 2.8 и определим их показания:

Таким образом, активная мощность трехфазной цепи

т.е. мощности, полученной при проверке баланса мощностей.

20

Для построения этой прямой достаточно двух точек: точку а, соответствующую Φ = 0 и А, и точку b, для которой U_м1 = 0, тогда и Вб.

Графики показаны на рисунке Б.5. Координаты точки пересечения характеристик дают значения магнитного потока Φ = 6,6∙10^-3 Вб и падения магнитного напряжения U_м1 = 320 А.

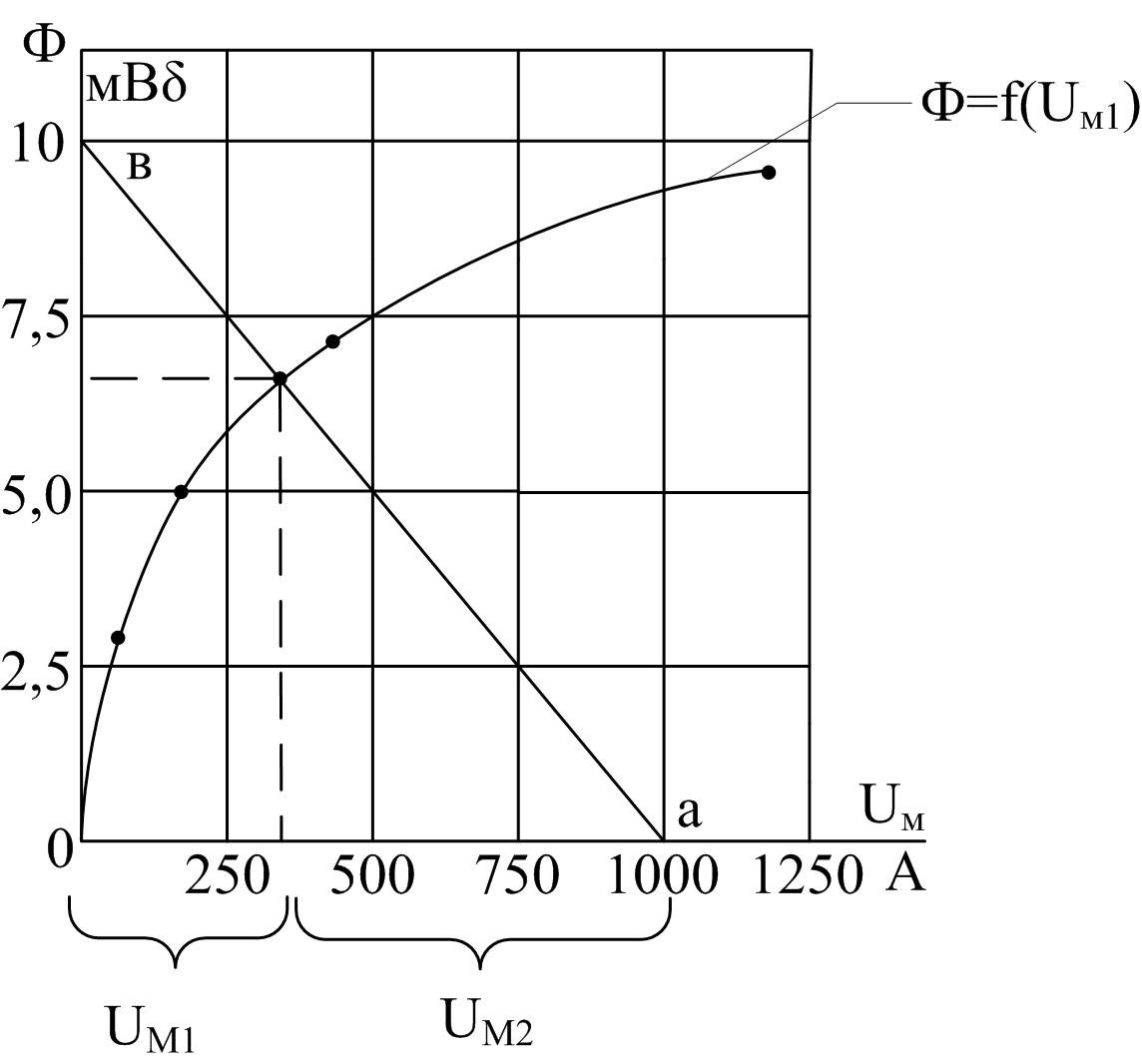
Рисунок Б.5

В воздушном зазоре U_м2=F – U_м1 = 1000 – 320 = 680 A.

Индукция в воздушном зазоре Тл.

Пример 4. Обратная задача. Магнитопровод разветвленной магнитной цепи выполнен из листовой электротехнической стали 1211. Геометрические размеры магнитной цепи (мм) показаны на рисунке Б.6. Величина воздушного зазора в среднем стержне δ = 0,15 мм. Число витков первой обмотки w₁ = 100, а второй обмотки w₂ = 200.

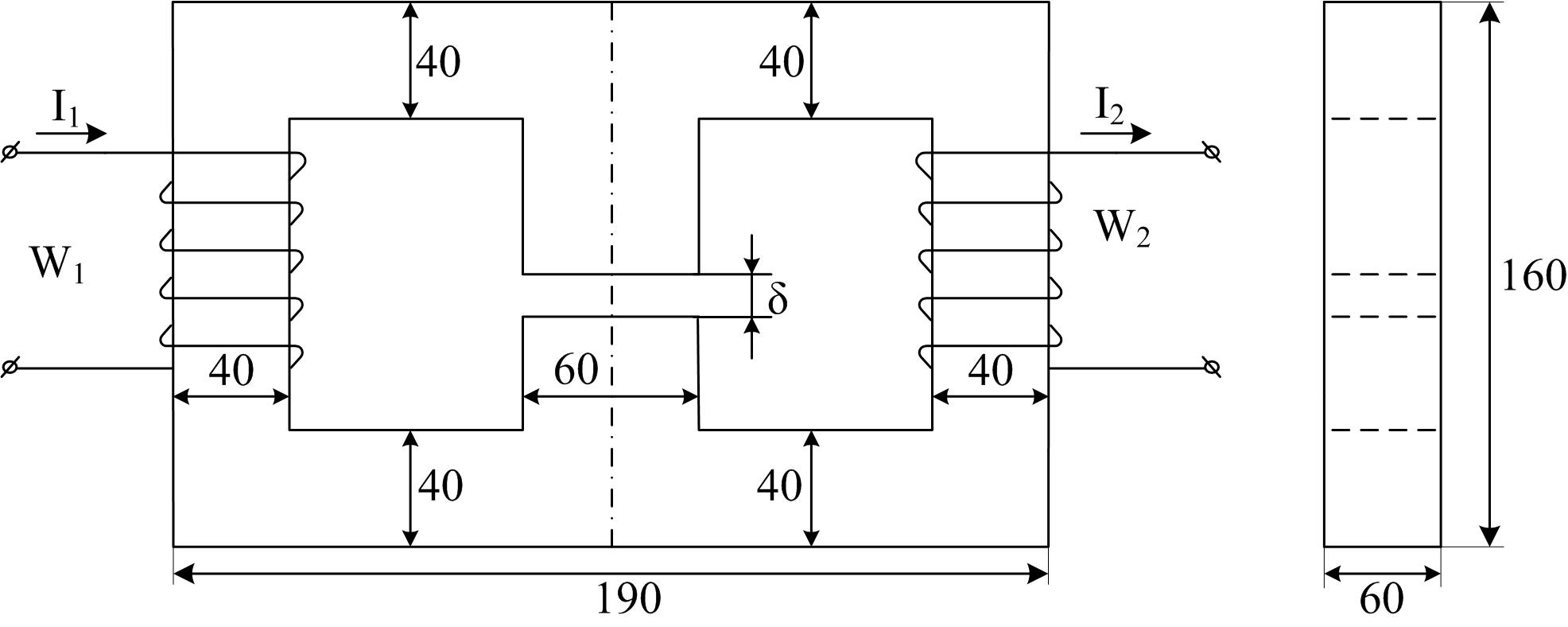
Рисунок Б.6

77

Второе слагаемое – то же на участке воздушного зазора

.

Получим следующее уравнение:

, или ,

где – МДС обмотки.

Здесь левая и правая части равенства – это U_м1. Получим два уравнения:

и .

Для графического решения задачи необходимо рассчитать и построить по этим уравнениям два графика зависимости Φ от U_м1 и найти координаты точки пересечения этих графиков, т.е. магнитный поток Φ и падение магнитного напряжения U_м1.

Рассчитаем магнитную характеристику, т.е. зависимости магнитного потока Φ от падения магнитного напряжения U_м1 на участке стали. Для этого задаемся несколькими значениями магнитного потока, определяем индукцию В и напряженность Н, затем вычисляем соответствующие им падения . Данные расчета сведены в таблицу Б.2.

Таблица Б.2

Φ, 10-4 Вб	, Тл	Н, А/м	, А
30	0,47	80	80
50	0,78	180	180
70	1,09	390	390
90	1,41	1200	1200

Зависимости Φ от U_м1 по второму уравнению изображается прямой линией, так как магнитное сопротивление воздушного зазора R_м – постоянная величина:

Гн^-1.

76

Построим векторную топографическую диаграмму (рисунок 2.12). Построение выполним в следующей последовательности:

1. На комплексной плоскости строим звезду фазных напряжений источника , предварительно выбрав масштаб напряжений.

2. Откладываем вектор смещения нейтрали и, соединив точку с точками А, В, С, получаем фазные напряжения потребителя: .

3. Под углами (аргументы сопротивлений ) к напряжениям строим векторы токов , предварительно выбрав масштаб токов.

4. От точки О´ откладываем напряжения под углом , (аргументы сопротивлений ) к токам и соединяем полученные точки соответственно с точками А, В, С. Итак, диаграмма построена.

Рисунок 2.12

2.2.2. Соединение нагрузки треугольником

Согласно заданным параметрам нарисуем схему трехфазной цепи при соединении нагрузки треугольником (рисунок 2.13).

21

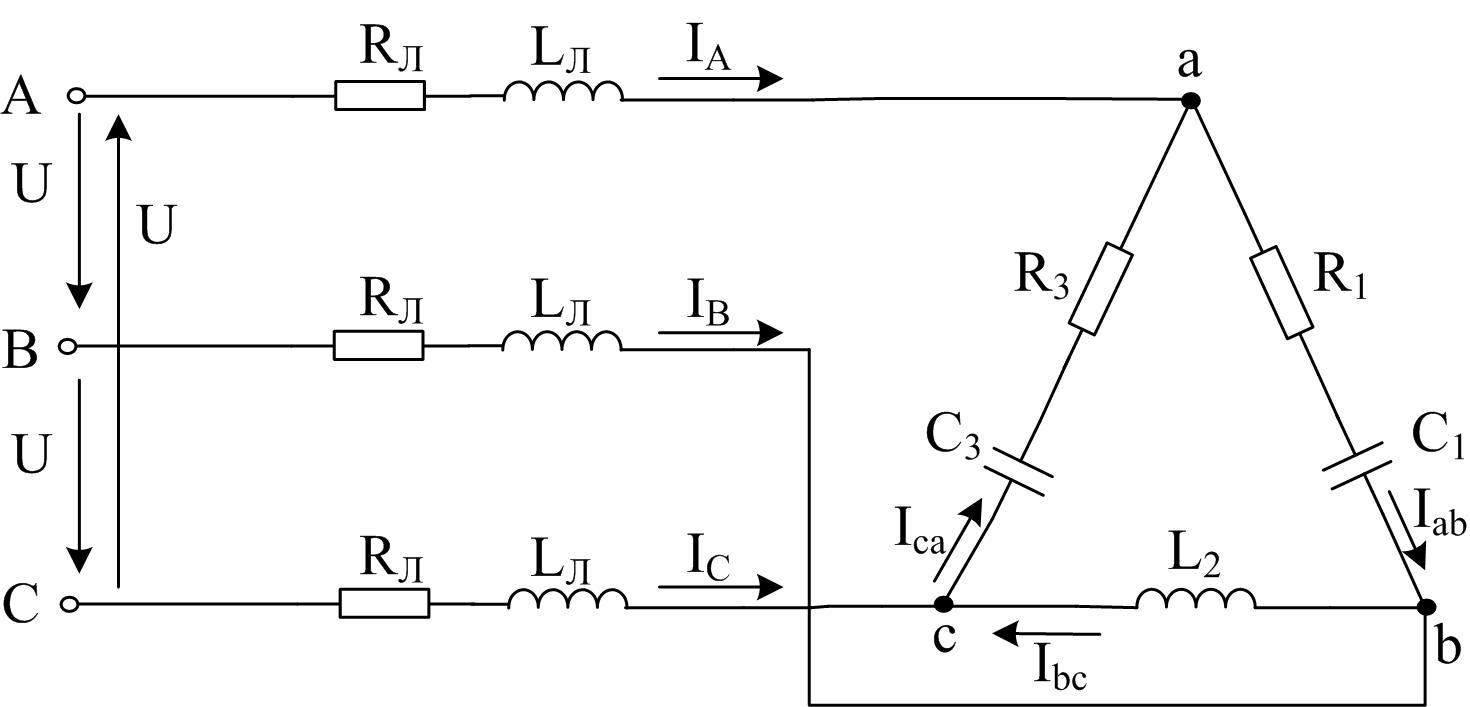
Рисунок 2.13

Решение. Определим сопротивления участков цепи:

где рад/см.

Комплексное сопротивление линии:

Ом.

Сопротивления фаз нагрузки:

Ом;

Ом;

Ом.

Преобразуем треугольник в эквивалентную звезду и получим схему (рисунок 2.14).

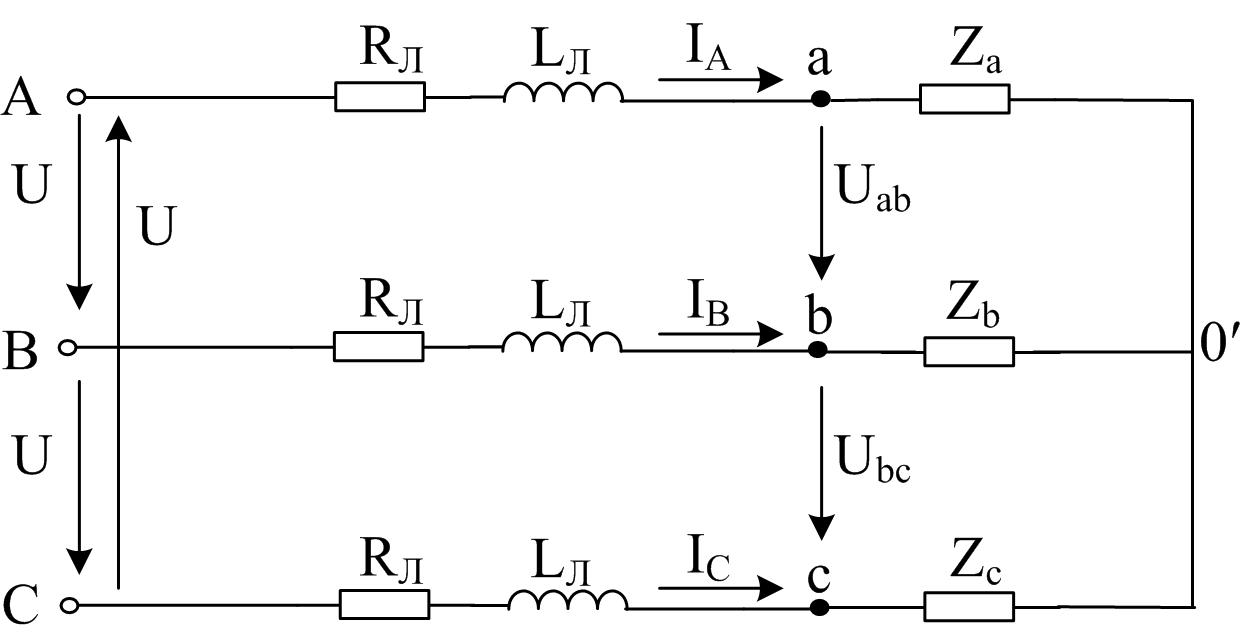
Рисунок 2.14

22

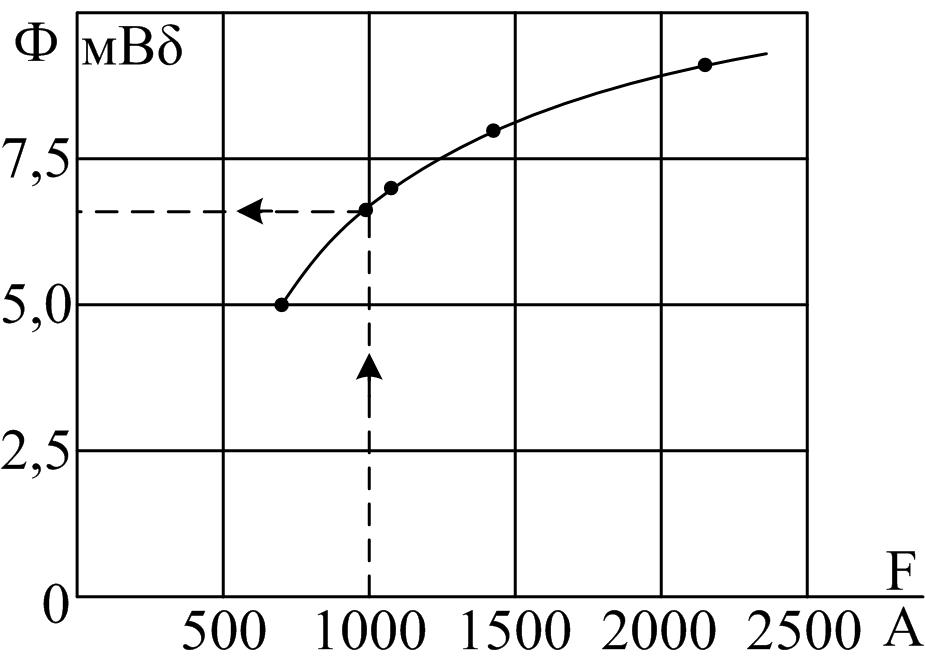
Рисунок Б.3

По характеристике находим, что заданному значению МДС F = 1000 А соответствует магнитный поток Φ = 6,6 мВб. Следовательно, индукция в воздушном зазоре

Тл.

Пример 3. Решить предыдущую задачу методом пересечений. Определить также падение магнитного напряжения в стали магнитопровода и в воздушном зазоре. Вычислить магнитную индукцию в зазоре.

Решение. По аналогии с нелинейными электрическими цепями составим схему замещения магнитной цепи (рисунок Б.4).

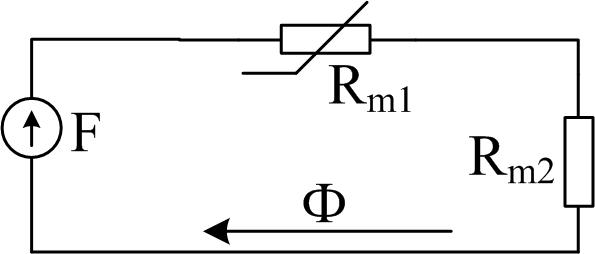
Рисунок Б.4

По закону полного тока для магнитной цепи

Первое слагаемое – это падение магнитного напряжения в стали магнитопровода:

75

Определим наибольшее возможное значение магнитного потока в этой цепи, пренебрегая магнитным сопротивлением стальной части магнитопровода. По закону Ома для магнитной цепи в этом случае

,

где – МДС обмотки;

– магнитное сопротивление воздушного зазора.

Примечание: такое же значение потока получим, если во втором законе Кирхгофа пренебречь падением магнитного напряжения в стали и определять напряженность , индукцию магнитный поток .

Так как стальная часть магнитопровода имеет некоторое магнитное сопротивление, то в этой магнитной цепи возможны магнитные потоки, меньше чем . В качестве расчетных значений магнитных потоков принимаем значения 9, 8, 7, 6 и 5 mВб. Решая для каждого значения магнитного потока прямую задачу (аналогично примеру 1), определим необходимые для их создания МДС. Данные расчета сведены в таблицу Б.1.

Таблица Б.1

Φ, мВб	, Тл	, Тл	H, A/м	Hδ, A/м	Hℓ, A	Hδδ, A	, A
9	1,41	1,41	1200	112,8	1200	902	2102
8	1,25	1,25	640	100,0	640	800	1440
7	1,09	1,09	390	87,2	390	698	1088
6	0,94	0,94	270	75,2	270	602	872
5	0,78	0,78	180	62,4	180	499	679

По данным таблицы Б.1 построим магнитную характеристику (рисунок Б.3). При ее построении можно ограничиться точками вблизи заданного значения МДС F = 1000 А.

74

Рассчитаем сопротивления фаз эквивалентной звезды:

Ом;

;

.

Расчет линейных токов произведем, как изложено выше в п. 2.2.1 – при соединении нагрузки звездой:

Ом;

Ом;

Ом.

Комплексы фазных напряжений источника:

Напряжение смещения нейтрали:

23

Фазные напряжения потребителя:

Линейные токи:

Проверим выполнение первого закона Кирхгофа:

.

Фазные напряжения в эквивалентной звезде нагрузки:

Определим линейные напряжения в эквивалентной звезде нагрузки (рисунок 2.14). Они же являются фазными напряжениями при соединении нагрузки треугольником (рисунок 2.13).

Токи фаз треугольника нагрузки:

24

.

Напряженность магнитного поля в магнитопроводе определим по кривой намагничивания (кривая 1, рисунок Б.2):

Н = 485 А/м.

Напряженность магнитного поля в воздушном зазоре

.

Требуемую МДС обмотки вычисляем на основании второго закона Кирхгофа для магнитной цепи:

Ток в обмотке

.

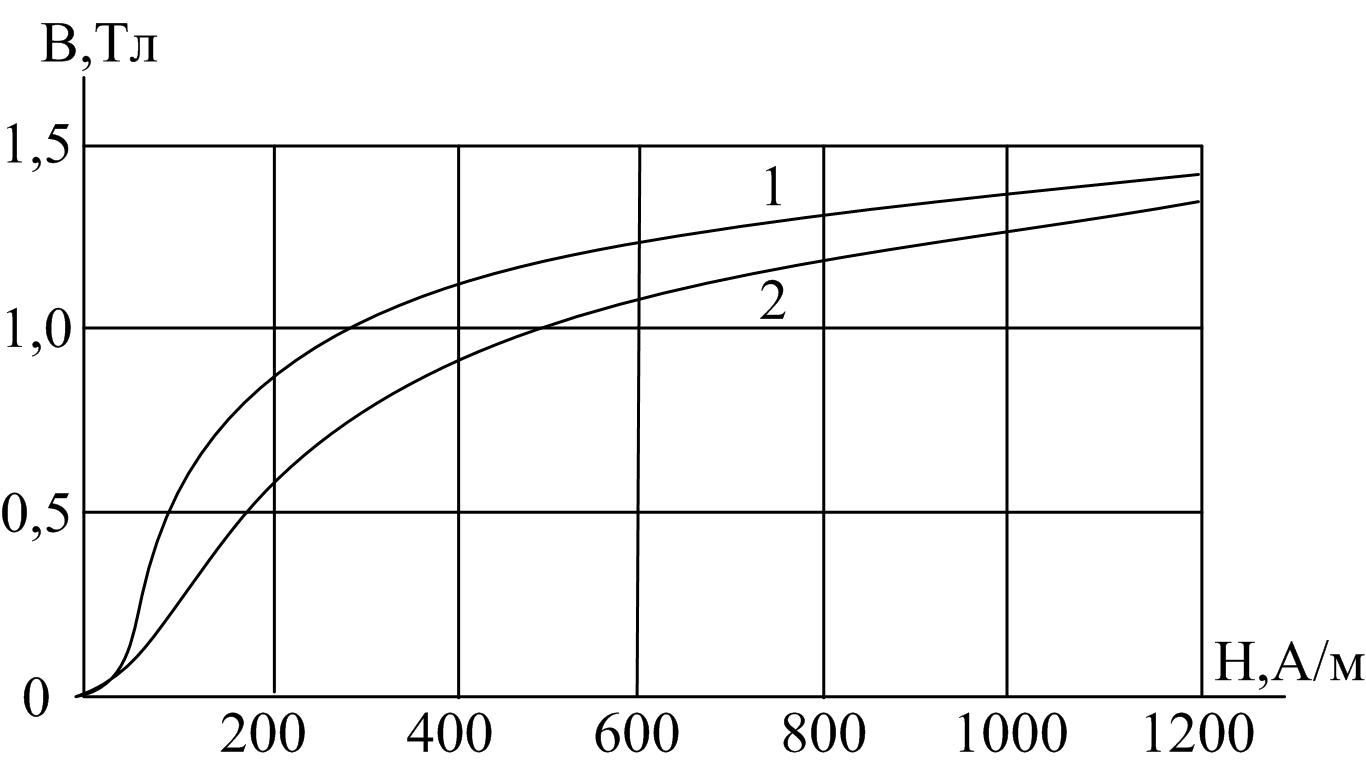
Рисунок Б.2

Пример 2. Обратная задача. Определить магнитную индукцию в воздушном зазоре магнитной цепи предыдущего примера, если ток в обмотке I = 1 А.

Решение. Эту обратную задачу расчета неразветвленной магнитной цепи можно решить построением магнитной характеристики цепи .

73

ПРИЛОЖЕНИЕ Б

Примеры решения прямой и обратной задач

Пример 1. Прямая задача. Определить ток в обмотке, требуемый для создания в неразветвленной магнитной цепи магнитного потока Φ = 75∙10^-4 Вб. Магнитопровод выполнен из электротехнической стали 1511. число витков обмотки w = 1000, величина воздушного зазора δ = 0,8 мм.

Размеры магнитопровода (мм) указаны на рисунке Б.1.

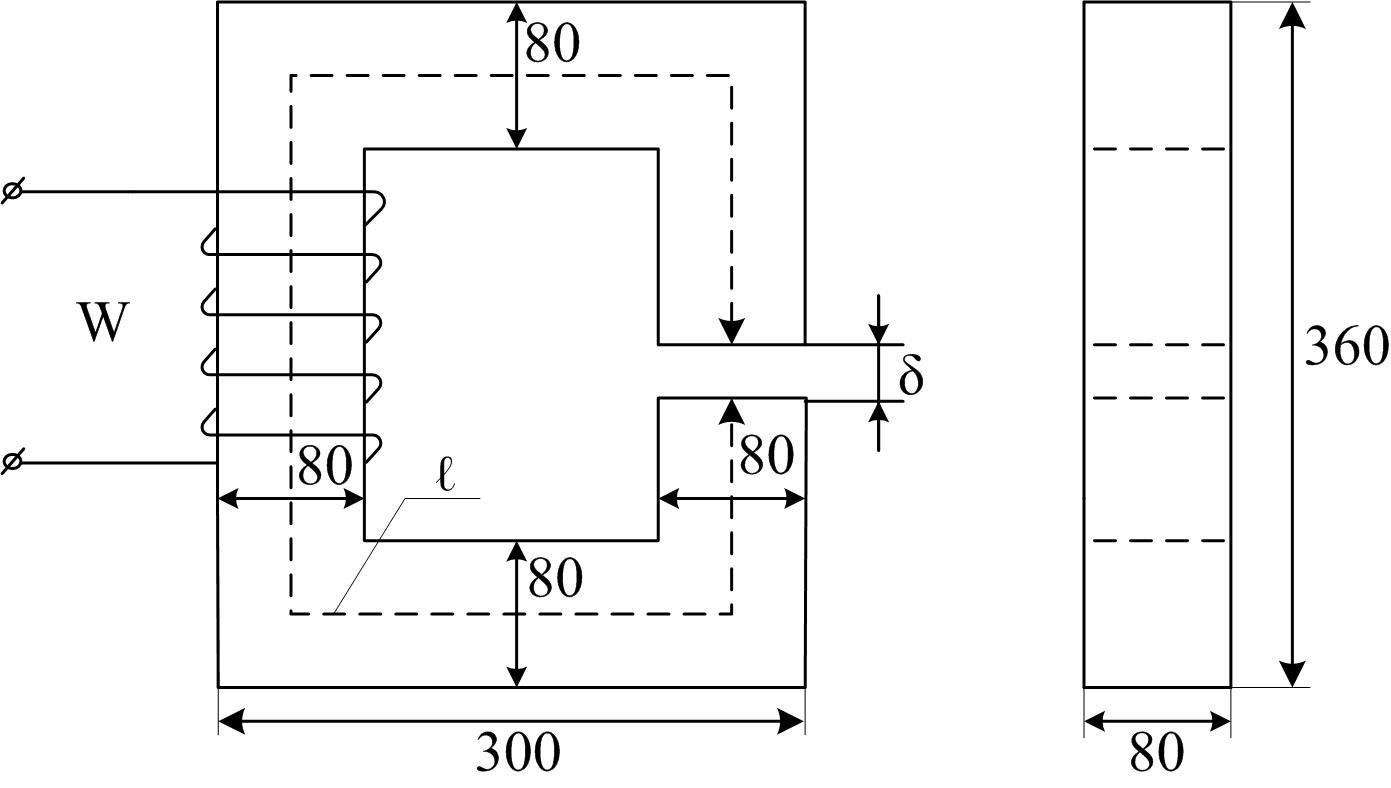
Рисунок Б.1

Решение. На эскизе магнитной цепи изобразим среднюю силовую линию и выделим однородные участки. Таких участков, очевидно, будет только два: один из них образуется стальной частью магнитопровода, а второй – воздушным зазором.

Определим геометрические размеры однородных участков длины:

;

.

«Выпучиванием» линии в зазоре пренебрегаем и считаем, что сечения магнитопровода и зазора равны:

.

Магнитная индукция однородных участков

72

Определим падения напряжения в линии:

Проверим баланс активных и реактивных мощностей. Комплекс полной мощности, вырабатываемой источником энергии:

Потребляемую мощность определим как сумму потребляемых мощностей в линии и в фазах нагрузки:

Баланс активных мощностей:

1092 Вт ≈ 1093 Вт.

Баланс реактивных мощностей:

845 ВАР ≈ 846 ВАР.

Таким образом, баланс активных и реактивных мощностей выполняется, что подтверждает правильность проведения расчетов.

Определим активную мощность методом двух ваттметров. Включим ваттметры, как показано на рисунке 2.8, и определим их показания:

25

Таким образом, мощность цепи, измеренная двумя ваттметрами, равна:

Вт,

что незначительно отличается от расчетной мощности (погрешность равна ).

Построим векторную топографическую диаграмму (рисунок 2.15).

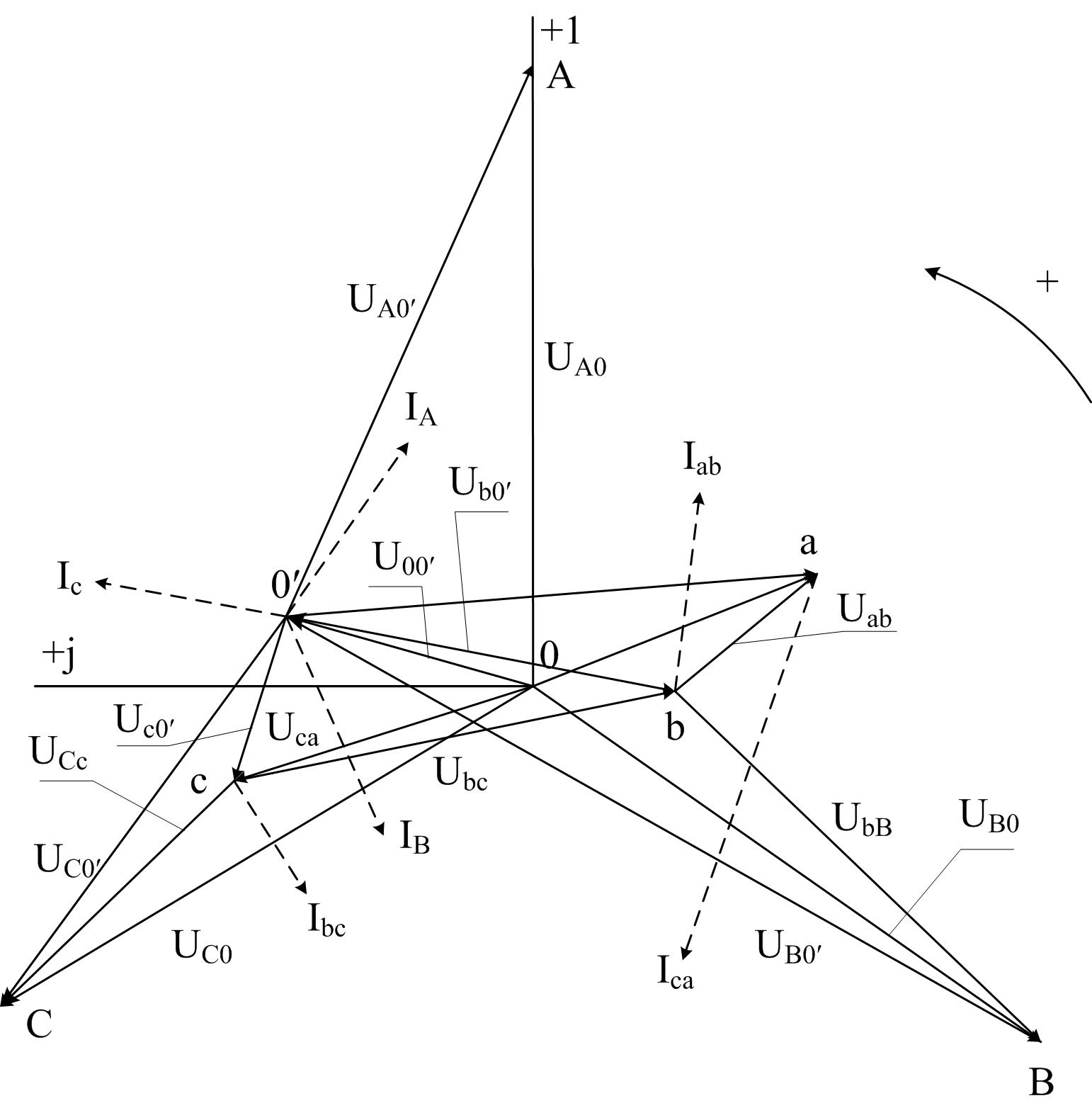
Рисунок 2.15

Построения выполним следующим образом:

1) На комплексной плоскости строим звезду фазных напряжений источника , предварительно выбрав масштаб напряжений.

2) Откладываем вектор смещения нейтрали и, соединив точку О´ с точками А, В, С, получаем фазные напряжения потребителя, фазы которого соединены звездой (рисунок 2.14), .

3) Под углами (аргументы сопротивлений ) к напряжениям строим векторы линейных токов , выбрав предварительно масштаб токов.

26

Продолжение таблицы А.1

вариант	U, B	Zл		Z1			Z2			Z3
		Rл, Ом	Lл, мГн	R1, Ом	L1, мГн	С1, мкФ	R2, Ом	L2, мГн	С2, мкФ	R3, Ом	L3, мГн	С3, мкФ
37	127	10	31.8	20	63.7	-	-	63.7	-	-	63.7	-
38	220	20	63.7	10	-	318	-	-	318	-	-	318
39	380	40	127	20	-	-	20	63.7	-	20	63.7	-
40	660	80	255	-	31.8	-	10	-	318	10	-	318
41	127	10	-	40	127	-	40	127	-	40	-	-
42	220	20	-	20	-	159	20	-	159	-	63.7	-
43	380	40	-	40	-	-	40	-	-	-	-	79.5
44	660	80	-	-	63.7	-	-	63.7	-	20	63.7	-
45	127	-	31.8	-	-	39.7	-	-	39.7	80	-	39.7
46	220	-	63.7	40	-	79.5	40	127	-	40	-	-
47	380	-	127	10	-	-	10	-	318	-	31.8	-
48	660	-	225	-	127	-	40	-	-	-	-	79.5
49	127	10	31.8	-	-	318	-	-	318	10	31.8	-
50	220	10	55.1	10	55.1	-	-	-	183.7	10	-	183.7

71

ПРИЛОЖЕНИЕ А

Таблица А.1

вариант	U, B	Zл		Z1			Z2			Z3
		Rл, Ом	Lл, мГн	R1, Ом	L1, мГн	С1, мкФ	R2, Ом	L2, мГн	С2, мкФ	R3, Ом	L3, мГн	С3, мкФ
1	127	10	31.8	10	-	-	10	-	318	10	-	-
2	220	10	55.1	-	55.1	-	10	-	-	-	55.1	-
3	380	20	110.3	-	-	91.8	-	110.3	-	-	-	91.8
4	660	80	225	80	225	-	-	-	39.7	80	255	-
5	127	10	-	20	-	159	20	63.7	-	20	-	159
6	220	10	-	-	110.3	-	20	110.3	-	20	-	-
7	380	20	-	-	-	183.7	10	-	183.7	-	55.1	-
8	660	80	-	10	31.8	-	10	-	-	10	-	318
9	127	-	31.8	40	-	79.5	-	127	-	40	127	-
10	220	-	55.1	10	-	-	10	-	-	10	-	183.7
11	380	-	110.3	20	-	91.8	20	-	-	20	-	-
12	660	-	255	20	63.7	-	-	63.7	-	-	63.7	-
13	127	10	31.8	80	-	39.7	-	-	39.7	-	-	39.7
14	220	20	63.7	20	-	-	20	63.7	-	20	63.7	-
15	380	40	127	-	127	-	40	-	79.5	40	-	79.5
16	660	80	255	40	127	-	40	127	-	40	-	-
17	127	10	-	10	-	318	10	-	318	-	31.8	-
18	220	20		40	-	-	40	-	-	-	-	79.5
19	380	40	-	-	255	-	-	255	-	80	255	-
20	660	80	-	-	-	39.7	-	-	39.7	80	-	39.7
21	127	-	31.8	20	-	159	20	63.7	-	20	-	-
22	220	-	63.7	80	-	-	80	-	39.7	-	255	-
23	380	-	127	-	31.8	-	10	-	-	-	-	318
24	660	-	255	-	-	318	-	-	318	10	31.8	-
25	127	10	31.8	40	127	-	-	-	79.5	40	-	79.5
26	220	10	55.1	20	-	-	20	-	91.8	20	-	-
27	380	20	110.3	-	55.1	-	10	-	-	-	55.1	-
28	660	80	255	-	-	159	-	63.7	-	-	-	159
29	127	10	-	80	225	-	-	-	39.7	80	255	-
30	220	10	-	10	-	183.7	10	55.1	-	10	-	183.7
31	380	20	-	-	110.3	-	20	110.3	-	20	-	-
32	660	80	-	-	-	79.5	40	-	79.5	-	127	-
33	127	-	31.8	10	31.8	-	10	-	-	10	-	318
34	220	-	55.1	20	-	91.8	-	110.3	-	20	110	-
35	380	-	110.3	10	-	-	10	-	-	10	-	183.7
36	660	-	255	80	-	39.7	80	-	-	80	-	-

70

4) От точки О´ откладываем напряжения фаз эквивалентной звезды под углами (аргументы сопротивлений ) к токам .

5) Соединив точки a, b, c соответственно с точками А, В, С получим падения напряжения .

6) Соединив между собой точки a, b, c, получим фазные напряжения нагрузки при соединении треугольником .

7) Под углами (аргументы сопротивлений ) к напряжениям строим фазные токи нагрузки . Диаграмма построена.