17) Движение воды на повороте русла.

Прогрессирующее искривление изогнутых участков речных русл, столь характерное для процесса меандрирования, есть следствие особенностей движения воды на участках изгиба. При переходе о прямолинейного участка к изогнутому высота свободной поверхности у внешнего (вогнутого) берега повышается, а у внутреннего (выпуклого) понижается. После скоростей потока сложным образом перестраивается. Чтобы уяснить природу этих явлений, сосредоточим внимание на вершине речной излучины, где кривизна русла наибольшая и влияние условий подхода исчезает. Для простоты предложим, что берега реки очерчены здесь по дугам концентричных окружностей. На плане участка возьмем произвольную точку М и проведем через нее траекторию частицы поверхностного слоя воды, предложив в первом приближении, что эта траектория также представляет собой дугу концентрической окружности (показана на рис. пунктиром). Радиус траектории обозначим r. Массу частицы положим равной единицы. Проведя через линию радиуса r вертикальную плоскость и применяя принцип Даламбера, рассмотрим условия динамического равновесия частицы в этой плоскости под действием силы тяжести g, центробежной силы инерции v²/r и силы взвешивающего давления воды 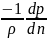, где V – скорость частицы и n – нормаль к свободной поверхности. Так как равнодействующая сил тяжести и инерции отклонена от вертикали на угол α, то на такой же угол должна быть отклонена от вертикали и сила давления. Но это значит, что линия свободной поверхности в рассматриваемой плоскости должна составлять угол α с горизонтом (рис б). Иначе говоря, условием динамического равновесия нашей частицы является существование радикального уклона свободной поверхности:

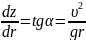
Если свободная поверхность в радикальном направлении перекошена, то в толще потока – вдоль всей вертикали – должен существовать радикальный градиент давления

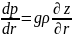
В потоке, где скорость течения по вертикали не изменяется, образование радикального градиента давления было бы единственным следствием кривизны траекторий жидких частиц. Эти частицы двигались бы по дугам окружностей и равновесие между центробежной силой и радикальным градиентом давления нигде бы не нарушалось. В любой точке потока равенство dр/dr=ρv²/r было бы справедливым.

В действительности, однако, дело обстоит не так. В потоках реальной жидкости скорость по вертикали меняется, а с ней, и притом более сильно, меняется пропорциональная квадрату скорости центробежная сила. Это обстоятельство вносит важные поправки в схему движения. Подробное рассмотрение вопроса с учетом изменения скоростей по глубине потока показывает, что радикальный уклон на данной вертикали ( в данной точке плана участка) устанавливается в соответствии со скоростью, близкой к средней на вертикали, т.е. выражается формулой:

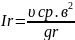
Следовательно, равновесие между силой инерции и радикальным градиентом давления имеется лишь в одной точке вертикали, где скорость близка к средней (т.е. на расстоянии от дна η≈0,4 h). Выше этой точки градиент давления не может уравновесить центробежные силы, и вода под их действием не может уравновесить центробежные силы, и вода под их действием получает компоненту скорости, направленную к вогнутому берегу. Действительная траектория поверхностной частицы воды показана на рис а) сплошной линией. Ниже точки равновесия, где центробежные силы малы, доминирующим делается влияние градиента давления и вода и течет к выпуклому берегу. В итоге в живом сечении образуется общее поперечное движение воды, направленное в верхних слоях к вогнутому, а в придонных к выпуклому берегу. У вогнутого берега движение воды является нисходящим. Сложение продольного и поперечного движений придает траекториям жидких частиц на изогнутом участке русла винтообразный характер. Приближенную величину поперечного уклона среднего по ширине сечения можно получить, заменив в формуле (57) среднюю скорость на вертикали средней скоростью в сечении V_ср и текущий радиус радиусом геометрической оси русла r₀ , т.е. применив формулу

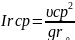
На достаточно крутых поворотах русла значения этого уклона могут быть близкими к значениям продольного уклона свободной поверхности. Поперечные течения, вызываемые центробежной силой, составляют внутренний механизм меандрирования. Скорости самих этих течений невелики – обычно они на порядок меньше продольных скоростей. Однако эти течения производят коренную перестройку поля продольных скоростей на изгибе русла. Поверхностное течение подводит к вогнутому берегу струи потока, обладающие наибольшей кинетической энергией. Смещение сюда максимума продольных скоростей вызывает размыв берега. Донное течение переносит продукты размыва к противоположному, выпуклому берегу. Искривленным участкам русл оказываются присущи резко несимметричные поперечные сечения с большими глубинами под крутым вогнутым берегом и пологим пляжным откосом у выпуклого берега. В ходе развития изогнутых участков рек кривизна русла и поперечные течения до определенного предела усиливают друг друга. Размыв потоком вогнутого берега увеличивает кривизну русла, а увеличение кривизны ведет к росту поперечного клона и усилению поперечного течения. Предел этому процессу кладется увеличением длин излучин, т.е. уменьшением в них продольных уклонов и соответствующим ослаблением скорости течения.