Логарифмічна міра добре відображає адитивність інформації.

Припустимо, що складне повідомлення складається з елементів .

_{Відомі імовірності} .

_{Імовірність складного повідомлення}

.

У теорії інформації використовують логарифм із підставами е й 2.

, .

Покладемо, що є два повідомлення та й відомі їхні апріорні ймовірності

тоді .

,

,

.

Якщо ,

.

За одиницю кількості інформації приймається кількість інформації, що втримується в повідомленні про одному із двох рівноможливих подій. Вона називається двійковою одиницею або біт.

2 .Джерело дискретних повідомлень і його ентропія

Покладемо, що ми маємо джерело дискретних повідомлень

Задано набір апріорних імовірностей передачі повідомлень .

Будемо вважати, що повідомлення джерела статистично незалежні, тобто ймовірності їхньої появи описуються одномірними безумовними ймовірностями . При цьому .

Можемо визначити кількість інформації, що втримується в кожному повідомленні джерела

.

Середня кількість інформації в одному повідомлені

Воно обчислюється виходячи з апріорних знань про ймовірність появи окремих повідомлень. Ця величина характеризує невизначеність стану джерела, тобто невизначеність того, яке з повідомлень з'явиться на його виході в розглянутий момент часу. Назвемо цю величину ентропією .

Покладемо, що є двійкове джерело повідомлень із апріорними ймовірностями .

.

Побудуємо графік ентропії у функції від .

Видно, що величина завжди позитивно й досягає максимуму при

Покладемо, що кількість повідомлень m. Тоді

.

З порівняння останніх двох виражень видно, що зі збільшенням кількості повідомлень джерела його ентропія зростає пропорційно . Звідси видно, що кількість інформації, що втримується в одному повідомленні джерела, росте зі збільшенням розміру алфавіту.

- ентропія нульового порядку, що`1 характеризує джерело статистичних незалежних рівномірних повідомлень.

Якщо , .

Обчислимо ентропію джерела не рівноімовірних незалежних повідомлень Коли, .

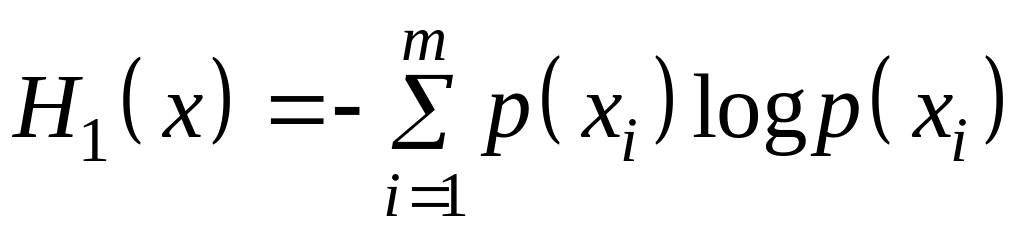Ентропію джерела не рівноімовірних попарно залежних повідомлень, позначимо , дамо розрахункову формулу

.

- характеризує джерело, у якого простежується зв'язок між ℓ – повідомленнями. Можна довести що

.

Таким чином, зі збільшенням статичних зв'язків між повідомленнями середня кількість інформації, що втримується в одному повідомленні, зменшується.

Надмірність повідомлень джерела повідомлень можна обчислити таким чином

.

Обчислимо надмірність джерела російської мови. Кількість символів алфавіту m=32, тобто у випадку рівноімовірніх символів

У російській мові простежуються статистичні зв'язку між 8 буквами, тобто при ℓ=8 .

Тоді надмірність .

Тобто при відповідному кодуванні блоками можна на 60% скоротити російські тексти, але цей шлях дуже складній, бо потребує введення спеціальних конструкцій (умовних скорочень) і має обмежені можливості. То того ж надмірність дає змогу корегувати помилки в каналах з завадами.