
- •1 Нормативні дані з дисципліни
- •2. Мета і завдання дисципліни
- •3 Перелік забезпечуючих дисциплін
- •4 Структура залікових кредитів
- •5 Навчально–методичне забезпечення дисципліни
- •5.1 Література
- •5.2 Методичні посібники та вказівки
- •Лекція 1 Система передачі інформації. Основні поняття і визначення
- •1. Місце інформаційних систем у сучасному світі
- •2. Класифікація систем передачі інформації
- •3. Узагальнена структурна схема системи передачі інформації
- •4.Основні інформаційно-технічні характеристики спи
- •4.1 Вірогідність передачі інформації
- •Завадостійкість передачі інформації
- •Швидкість передачі інформації
- •Пропускна здатність каналів зв'язку
- •Висновки
- •Тестові запитання
- •1.Кількість інформації в повідомленні
- •Логарифмічна міра добре відображає адитивність інформації.
- •2 .Джерело дискретних повідомлень і його ентропія
- •Ентропію джерела не рівноімовірних попарно залежних повідомлень, позначимо , дамо розрахункову формулу
- •3.Джерело неперервних повідомлень
- •Висновки
- •Тестові запитання
- •Практичне заняття №1
- •Задачі для самостійного розв’язання
- •Лекція 3 Передача інформації з дискретними і неперервними каналами зв'язку
- •1.Продуктивність джерела дискретних повідомлень
- •2.Швидкість передачі інформації з дискретних каналів без перешкод. Оптимальне статистичне кодування
- •3.Швидкість передачі інформації й пропускна здатність дискретних каналів з завадами
- •4.Пропускна здатність двійкового симетричного каналу зв'язку з завадами
- •5.Швидкість передачі інформації неперервними каналами з завадами.
- •6. Пропускна здатність неперервного каналу з нормальним білим шумом
- •Пропускна здатність неперервного каналу зв'язку при довільних спектрах сигналів і завад.
- •Висновки
- •Тестові запитання
- •Практичне заняття №2
- •Задачі для самостійного розв’язання
- •Лекція 4 завадостійке кодування. Основні положення теорії завадостійкого кодування
- •1.Постановка задачі застосування завадостійких кодів
- •2.Класифікація завадостійких кодів
- •3. Основні числові характеристики завадостійких кодів
- •4.Кодова відстань і її зв'язок із кратністю помилок що виявляються й або, що виправляються.
- •Висновки
- •Лекція 5 Систематичні блокові лінійні коди
- •Загальні методи кодування і декодування систематичних блокових лінійних кодів
- •Код з парним числом одиниць
- •Інверсний код
- •Код з подвоєнням елементів
- •Коди Хемінга
- •Висновки
- •Лабораторна робота №1 вивчення принципу дії та дослідження завадостійкості радіосистеми передавання інформації із блоковим кодом
- •1 Мета роботи
- •2 Методичні вказівки
- •Позиції, що займають одиниці в одиничній матриці, вказують номера позицій контрольних символів, що використовуються у кожній перевірці на парність.
- •3 Опис лабораторної установки
- •4 Порядок виконання роботи
- •6 Контрольні запитання і завдання
- •Лекція 6 циклічні коди
- •Основні властивості циклічного коду й способи побудови
- •Способи кодування і декодування циклічних кодів
- •Матричне подання циклічних кодів
- •Висновки
- •Тестові запитання
- •Лабораторна робота №2 Вивчення властивостей і принципів побудови циклічних кодів.
- •1 Ціль роботи
- •2 Методичні вказівки
- •3 Порядок виконання роботи
- •5 Контрольні запитання.
- •Практичне заняття №3
- •Розв’язання. Визначимо кількість інформаційних і контрольних символів у кодовій комбінації:
- •Задачі для самостійного розв’язання
- •Лекція 7 Оптимальний когерентний прийом дискретних сигналів
- •1.Основні положення теорії оптимального приймання сигналів
- •Синтез, правила розрізнення сигналів у випадку приймання повністю відомих сигналів на фоні нормального білого шуму
- •Структурні схеми оптимальних приймачів
- •Обчислення завадостійкості (імовірності помилок розрізнення сигналів) оптимальних когерентних приймачів
- •Виходячи з цього, можна записати формули для обчислення імовірностей помилок в системах когерентного приймання фазовою, частотною та амплітудною маніпуляцією.
- •Висновки
- •3 Порядок виконання роботи
- •5 Контрольні запитання
- •Лекція 8 оптимальний некогерентний прийом дискретних сигналів і його завадостійкість
- •Модель лінії зі змінними параметрами
- •Алгоритм прийняття рішення при прийманні сигналів з випадковою початковою фазою
- •Приймання сигналів з випадковою початковою фазою і флуктуючою амплітудою
- •Некогерентні приймачі сигналів з використанням обробки за огинаючою
- •Некогерентний приймач ортогональних сигналів
- •Приймання сигналів з випадковою початковою фазою при використанні відносної фозової маніпуляції
- •Висновки
- •Тестові запитання
- •3 Порядок виконання роботи.
- •4 Структура звіту
- •5 Контрольні запитання і завдання
- •Практичне заняття № 4 "Когерентне и не когерентне приймання дискретних сигналів та його завадостійкість"
- •Приклади розв’язання основних типів задач
- •Задачі для самостійного розв’язання
- •Лекція 9 оптимальний і квазиоптимальНіЙ прийом неПерервних сигналів і його завадостійкість
- •1.Особливості приймання неперервних сигналів з аналоговою модуляцією
- •2. Завадостійкість прийому сигналів з амплітудною модуляцією
- •3.Завадостійкість прийому сигналів з фазовою модуляцією
- •4.Завадостійкість прийому сигналів з частотною модуляцією
- •Висновки
- •Лекція 10 цифрові методи передачі неЗперервних повідомлень
- •Імпульсно – кодова модуляція
- •2.Завадостійкисть систем зв’язку з імпульсно-кодовою модуляцією
- •3.Диференціальна імпульсно-кодова модуляція. Дельта модуляція
- •Висновки
- •Тестові запитання
- •Практичне заняття № 5
- •Приклади розв’язання основних типів задач
- •Задачі для самостійного розв’язання
- •Лекція 11 багатоканальні системи передачі інформації
- •1.Узагальнена структура багатоканальної системи зв’язку
- •2.Системи зв’язку із частотним поділом каналів
- •3Системи зв’язку із часовим поділом каналів
- •Висновки
- •Тестові запитання
- •Лекція 12
- •1. Поняття про багатостанційний доступ
- •Системи з часовим поділом каналів
- •Системи із частотним поділом каналів
- •Системи з кодовим поділом каналів
- •Асинхронно-адресні системи передачі інформації (аас)
- •Висновки
Висновки
В лекції розглянуті методи приймання сигналів в каналах із змінними параметрами, наведені структурні схеми приймачів із випадковою початковою фозою і флуктуючою амплітудою. Показано, що флуктуації параметрів сигналу приводять до суттєвого зниження завадостійкості. Наведені розрахункові формули імовірності помилок розрізнення сигналів.
Тестові запитання
1. Маємо
сукупність причин
![]() ,
,
![]() та сукупність наслідків
та сукупність наслідків
![]() ,
,
![]() .
Яка з формул дозволяє обчислити
апостеріорну імовірність причин
.
Яка з формул дозволяє обчислити
апостеріорну імовірність причин
![]() ,
якщо спостерігається наслідок
?
,
якщо спостерігається наслідок
?
1)
![]()
2)

3)
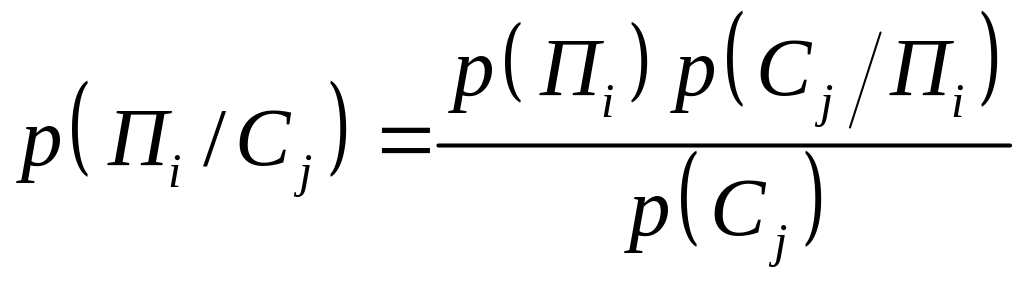
2.
Передається дискретне повідомлення
![]() із алфавіта
,
приймається його оцінка
із алфавіта
,
приймається його оцінка ![]() .
Як співвідносяться апостеріорна
імовірність
.
Як співвідносяться апостеріорна
імовірність ![]() і апріорна
і апріорна
![]()
![]()
![]()
3. Апріорна
імовірність передавання повідомлення
![]() ;
імовірність переходу
;
імовірність переходу ![]() імовірність приймання
імовірність приймання ![]() .
Чому дорівнює апостеріорна імовірність
передавання
.
Чому дорівнює апостеріорна імовірність
передавання ![]() ?
?
0,4
0,5
0,6
0,7
4. Яка з формул визначає правило рішення при прийманні дискретних сигналів по критерію Байєса ?
![]()
![]()
![]()
![]()
5. Яка з формул визначає правило рішення приймача дискретних сигналів по критерію максимальної правдоподібності?
1)
![]()
![]()
![]()
![]()
6. При якому законі розподілу апріорних імовірностей рішення по критерію Байєса і критерію максимальної правдоподібності дає однаковий результат?
закон Гауса
закон рівних імовірностей
закон Релея
7. Яка імовірність в теорії рішень має назву “функція правдоподібності”?
1)
![]()
2)
![]()
3)
4) ![]()
8. По
системі зв’язку передається інформація,
яка формується повідомленнями з алфавіту
х1...х4,
апріорні імовірності яких однакові.
Відома матриця імовірностей переходів
![]() ,
фрагмент якої при прийманні
,
фрагмент якої при прийманні
![]() має вигляд
має вигляд ![]() ;
;
![]() ;
;
![]() ;
;
![]() .
Яке передане повідомлення зафіксує
оптимальний приймач?
.
Яке передане повідомлення зафіксує
оптимальний приймач?
х1
х2
х3
х4
9. Система передачі дискретних повідомлень характеризується матрицею імовірностей переходів.

Яка сукупність імовірностей має максимальні значення?
![]()
![]()
![]()
10. По
каналу зв’язку передаються повідомлення
і
з
апріорними імовірностями
![]() і
і
![]() .
Відома матриця імовірностей переходів
.
Відома матриця імовірностей переходів
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
Чому дорівнює апостеріорна імовірність
передавання х1,
якщо прийнято повідомлення
?
.
Чому дорівнює апостеріорна імовірність
передавання х1,
якщо прийнято повідомлення
?
0,06
0,07
0,24
0,63
11. Якою з формул визначається середня імовірність помилки при когерентному прийманні дискретного ФМ сигналу?
1)
![]()
2)
![]()
3)
![]()
12. Якою з формул визначається середня імовірність помилки при когерентному прийманні дискретного ЧМ сигналу?
1)
2)
3)
13. Якою з формул визначається середня імовірність помилки при когерентному прийманні дискретного АМ сигналу?
1)
2)
3)
14.
Який вигляд має функція Крампа
![]() ?
?
1)

2)

3)

15. Який вигляд має правило рішення по критерію максимума правдоподібності при прийманні рівноімовірних дискретних сигналів?
1)

2)

3)

16. Який вигляд має імпульсний відгук оптимального узгодженого фільтра?
1)
![]()
2)
![]()
3)
![]()
17. Яке співвідношення пов’язує тривалість дискретного сигналу Тс і ширину смуги пропускання оптимального фільтра, узгодженого по ширині смуги?
1)
![]()
2)
![]()
3)
![]()
18. Чому
повинна дорівнювати ширина смуги
пропускання оптимального фільтра,
узгодженого по смузі, якщо тривалість
сигналу
![]()
1)
![]()
2)
![]()
3)
![]()
19. На вхід оптимального узгодженого фільтра надходить прямокутний радіоімпульс тривалістю Тс . Чому дорівнює тривалість вихідного сигналу?
1) Тс
2Тс
3Тс
20. Яке співвідношення між вхідними відношеннями сигнал/шум необхідне для забезпечення рівних імовірностей помилкового приймання сигналів АМ, ЧМ і ФМ?
1)
 ,
,
 ,
,

2)
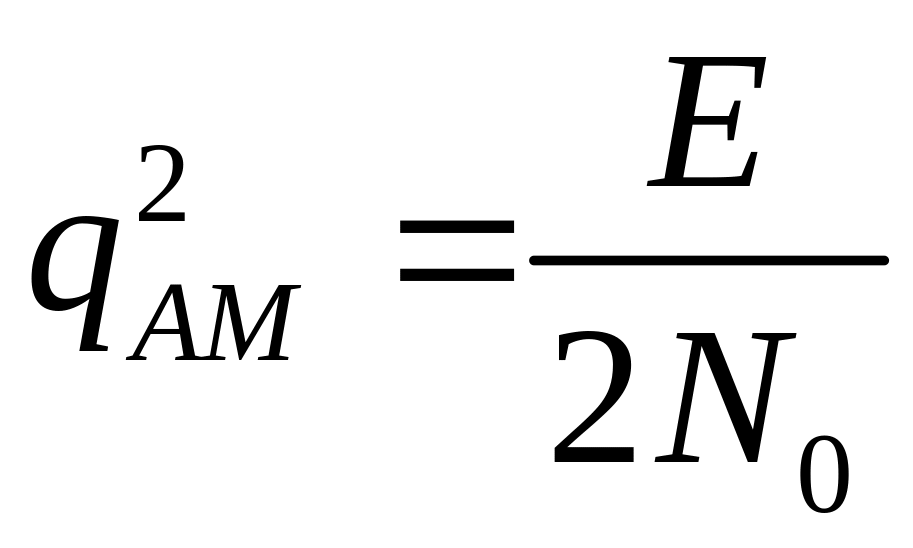 ,
,
 ,
,

3)
,
,

21. Який вид модуляції сигналів застосовується для боротьби з випадковою початковою фазою сигналів?
АМ
ЧМ
ФМ
ВФМ
22. Який вид модуляції сигналів найбільш придатний для застосування в каналах зв’язку з випадковою початковою фазою і флуктуючою амплітудою?
1) АМ 2) ЧМ
3) ФМ
4) ВФМ
23. Якою з формул визначається імовірність помилки некогерентного приймання двійкових АМ сигналів?
1)
![]()
2)
![]()
3)
![]()
24. Якою з формул визначається імовірність помилки некогерентного приймання двійкових ЧМ сигналів?
1)
2)
3)
25. Якою з формул визначається імовірність помилкового приймання двійкових ВФМ сигналів методом порівняння фаз?
1)
2)
3)
26. По
системі зв’язку передаються сигнали
![]() і
і
![]() з відомими апріорними ймовірностями
з відомими апріорними ймовірностями
![]() і
і
![]() та ймовірностями хибних переходів
та ймовірностями хибних переходів
![]() і
і
![]() .
Чому дорівнює середня імовірність
помилкового приймання?
.
Чому дорівнює середня імовірність
помилкового приймання?
1)
![]()
2)
![]()
3)
![]()
4)
![]()
27. Яке співвідношення між вхідними відношеннями сигнал/шум необхідне для забезпечення рівних імовірностей помилки некогерентного приймання сигналів АМ, ЧМ, ВФМ?
1)



2)

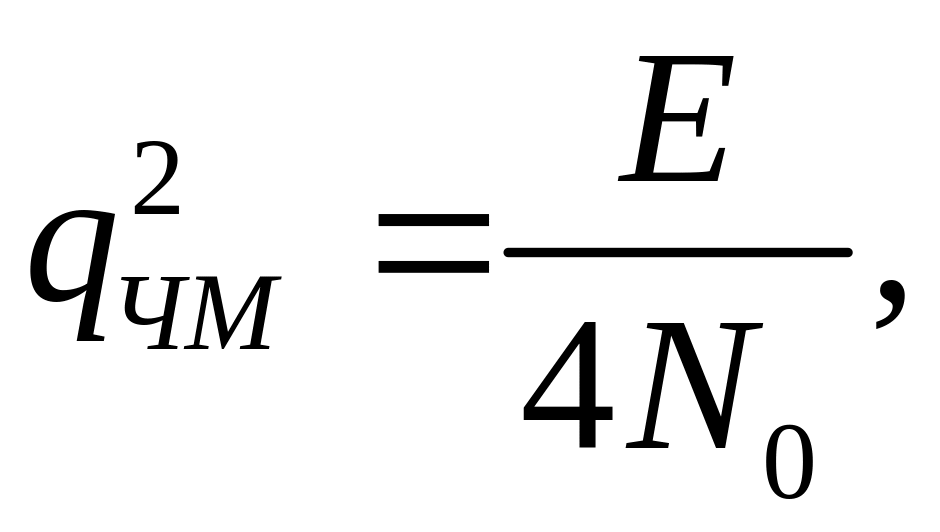

3)
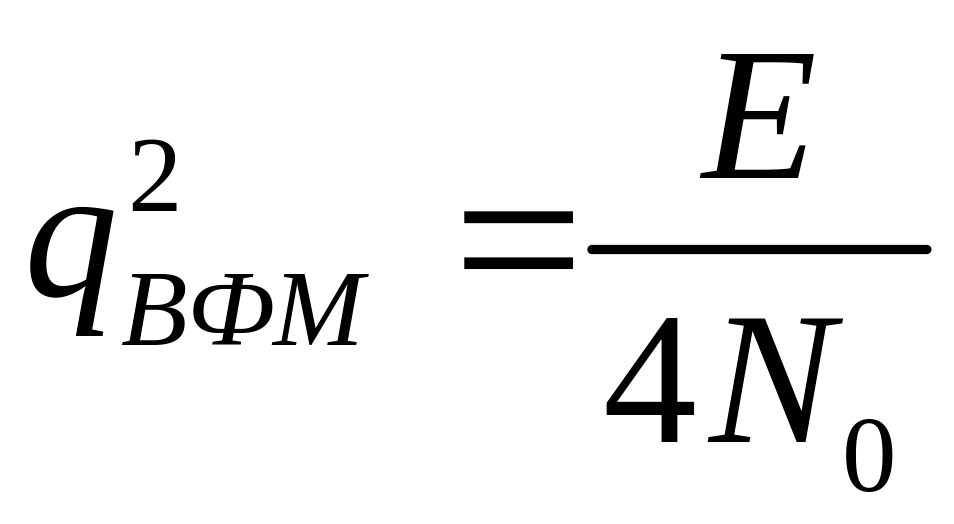
28. Яке
відношення сигнал/шум
![]() необхідно забезпечити на вході
некогерентного приймача АМ сигналів,
якщо задана імовірність помилкового
приймання
?
необхідно забезпечити на вході
некогерентного приймача АМ сигналів,
якщо задана імовірність помилкового
приймання
?
1)
![]()
2)
![]()
3)
![]()
29. Яке відношення сигнал/шум необхідно забезпечити на вході некогерентного приймача ЧМ сигналів, якщо задана імовірність помилкового приймання ?
1)
![]()
2)
![]()
3)
![]()
30. Яке відношення сигнал/шум необхідно забезпечити на вході приймача ВФМ сигналів, якщо задана імовірність помилкового приймання ?
1)
2)
3)
лАБОРАТОРНА РОБОТА № 4
Дослідження некоГЕРЕНТНОГО приймача двійкових радіосигналів і його завадостійкості
1 Ціль роботи
Дослідження принципів функціонування некогерентного приймання приймачів двійкових сигналів, завадостійкості приймачів, порівняння результатів експериментальних досліджень з теоретично досяжними можливостями.
2 Методичні вказівки
При підготовці до виконання лабораторної роботи необхідно вивчити тему 14 по конспекту лекцій та рекомендовану літературу [1, c. 93-102; 2, с. 178 - 158; 5, с. 164 - 167; 6, с. 168 – 183]. Особливу увага звернути на наступні основні положення.
В лабораторній роботі №4 розглянуті теоретичні засади приймання дискретних радіосигналів у випадку, коли лінія зв’язку тільки послаблює сигнал, не змінюючи його форми, тобто випадок приймання сигналів з повністю відомими параметрами. В реальних умовах форма сигналу спотворюється. Якщо послаблення сигналу а – випадкова величина, що повільно змінюється, але практично постійна на інтервалах Тс приймання здійснюється за вирішуючим правилом
R=max
p(xi)w![]() (5.1)
(5.1)
При випадковому значенні а необхідно осереднити результат за законом розподілу w(a), тоді при рівно імовірних сигналах вирішуючи правило прийме вигляд
![]() (5.2)
(5.2)
Із співвідношення (5.2) витікає, що при такому підході структура оптимального приймача залишиться такою ж, як і у випадку цілком відомих сигналів.
Імовірність помилкового приймання протилежних сигналів у випадку, коли розподіл w(a) за законом Релея, обчислюється за формулою
![]()
де
![]()
Розглянемо далі випадок, коли лінія вносить в сигнали тільки випадковий зсув початкової фази, що має місце в переважній більшості реальних ситуацій. При цьому, якщо
S(t,xi)=Scosit
(0<t![]() Tc),
Tc),
Сигнали на виході лінії (вході приймача)
Sвих(t,xi)=Scos(it-0) (5.3)
Вихідні сигнали (5.3) можна подати у вигляді двох складових із випадковими амплітудами, але постійними фазами
S(t,xi)=Scoscosit-Ssinsinit=bScosit-c Ssinit, (5.4)
Із (5.4) видно, що спотворюючу дію лінії можна звести до появи в точці приймання двох складових сигналу: косинусоїдниї та синусоїдної. Алгоритм роботи приймача в цьому випадку
 (5.5)
(5.5)
Із цього виразу видно, що оптимальний приймач виконує кореляцію прийнятої реалізації y(t) із зразками обох складових сигналу (5.4). Зведення результатів у квадрати перед складанням та виборам максимуму викликано тим, що величини b та с можуть бути як позитивними, так і негативними. Структурна схема, яка відповідає алгоритму (5.5) при М=2, наведена на рис. 5.1а. Цей алгоритм можна реалізувати також і за допомогою узгоджених фільтрів та детекторів огинаючих вихідних коливань (рис. 5.1б), після яких і береться відлік.
 а)
а)

б)
Рисунок 5.1 – Структурні схеми оптимальних приймачів при невідомій початковій фазі сигналів, реалізованих на основі кореляційної обробки (а) та на основі узгоджених фільтрів (б).
Фізика процесів також зрозуміла: якщо на вхід узгодженого з сигналом S(t,xi) фільтра подати зсунутий по фазі сигнал, то завдяки лінійності фільтра має місце затримка коливання на виході фільтра. Тому відлік в момент t=Tc не співпадає з максимумом напруги. Враховуючи випадковість цього зсуву найкращою стратегією є відлік огинаючої, а не миттєвого значення коливання.
Співставимо випадок приймання сигналів при відсутності випадкової фази (тобто точно відомих по формі сигналів) і при наявності випадкової фази. Перший випадок прийнять називати когерентним, другий – некогерентним прийманням. Некогерентне приймання найчастіше застосовується в реальних системах зв’язку.
При некогерентному прийманні ортогональних сигналів (частотній маніпуляції) імовірність помилки дорівнює
![]() (5.6)
(5.6)
При некогерентному прийманні амплітудно-маніпульованих сигналів
![]() (5.7)
(5.7)
Співставляючи вирази при однакових значеннях імовірності помилки, можна встановити, який енергетичний програш дає застосування некогерентного приймання у порівнянні з когерентним. Розрахунки показують, що для забезпечення ре=10-3...10-6 при некогерентного прийманні необхідно збільшувати енергію сигналу на 15-30% у порівнянні з когерентним, тобто програш невеликий.
У більш загальному випадку неідеальність лінії обумовлює випадкові зміни амплітуди і фази. Імовірність помилок при цьому збільшується, тому що незалежно діють обидва розглянутих фактори. Можна показати, що в цьому випадку імовірність помилок при розпізнаванні бінарних ортогональних сигналів (частотна маніпуляція) дорівнює
![]()
де
![]() – середнє значення енергії сигналів,
що приймаються.
– середнє значення енергії сигналів,
що приймаються.
