Практичне заняття №2
«Передача інформації з дискретним і безперервним каналах зв'язку»
Мета - з використанням вивченого теоретичного матеріалу навчитися обчислювати швидкість передачі дискретної і безперервної інформації по каналах зв'язку, пропускну здатність дискретних та неприривного каналів зв'язку, ефективність узгодження джерел інформації з пропускною здатністю каналів. Спочатку приводяться приклади розв'язання типових практичних завдань, потім формуєте умови задач для самостійного рішення, причому числові значення для вирішення завдань дано в 10 варіантах.
Приклад 1
Повідомлення джерела формуються із
символів алфавіту m=8.
Тривалість кожного символу
=10
мс. Визначити швидкість передавання
символів і швидкість передавання
інформації.
Розв’язання. Швидкість передавання сигналів
.
Швидкість передавання інформації
біт/с.
Приклад 2.
Кількість символів алфавіту m=4.
Імовірності появи символів дорівнюють
відповідно
.
Тривалості символів
с;
с;
с;
с.
Чому дорівнює швидкість передавання
інформації при використанні таких
символів?
Розв’язання.
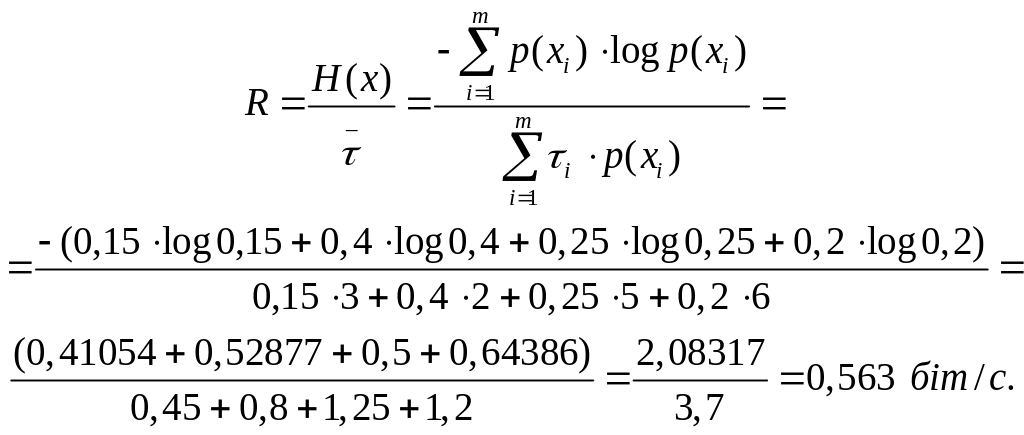
Приклад 3.
Повідомлення передаються двійковим
кодом (m=2).
Тривалість символу 0
с,
тривалість символу 1
с.
Визначити швидкість передавання
інформації для таких випадків: а) символи
рівно імовірні і незалежні; б) імовірності
появи символів
;
в)
;
;
г)
;
.
Розв’язання.
а) символи рівноімовірні і незалежні
;
б)
в)
.
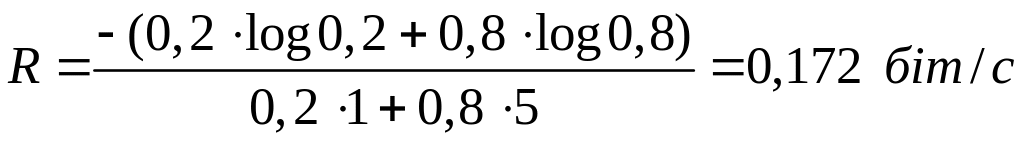г)
.
Приклад 4. Чому дорівнює пропускна здатність бінарного симетричного каналу, якщо в результаті дії завад 3% прийнятих повідомлень спотворені, а джерело виробляє повідомлення із швидкістю V=10 символів за секунду?
Розв’язання.
Приклад 5.
Чому дорівнює пропускна здатність
симетричного каналу, якщо джерело
виробляє із швидкістю 10 символів за
секунду повідомлення, закодовані кодом
з основою m=10,
а імовірність помилкового приймання
.
Розв’язання.
Приклад 6. Повідомлення дискретного джерела кодуються рівномірним двійковим кодом і передаються симетричним каналом зв’язку з завадами. Визначити пропускну здатність каналу зв’язку за умови, що тривалість двійкових сигналів = 1 мкс, середня імовірність помилки на один двійковий символ .
Розв’язання. Пропускна здатність двійкового симетричного каналу обчислюється за формулою
Приклад 7. Джерело,
яке виробляє 4 повідомлення
з апріорними імовірностями
;
;
та
підключене до каналу передавання
інформації, який має пропускну здатність
.
Передавання інформації здійснюється
рівномірним кодом.
З якою швидкістю буде здійснюватися передавання інформації при відсутності завад?
Розв’язання. Ентропія повідомлень визначається за формулою
Швидкість
передавання повідомлень
може бути визначена із виразу для
пропускної здатності каналу
.
Таким чином швидкість передавання інформації
.
Приклад 8. Скільки
в середньому можна передати літер
українського тексту в секунду по каналу
без завад з пропускною здатністю
,
якщо здійснюється ефективне статистичне
кодування.
Розв’язання.
При ефективному
статистичному кодуванні середня довжина
кодової комбінації (середня кількість
розрядів) дорівнює ентропії джерела. В
українській мові ентропія на одну букву
з урахуванням всіх статистичних зв’язків
дорівнює приблизно
.
Тому середня швидкість передавання українського тексту:
Приклад 9. При
передаванні неперервних сигналів
каналом зв’язку здійснюється
імпульсно-кодова модуляція. Дискретизація
за часом виконується з частотою
.
При квантуванні за рівнем шкала рівнів
ділиться на 128 дискретних рівнів.
Визначити пропускну здатність каналу без завад.
Розв’язання. Кількість дискретних рівнів визначає кількість повідомлень, які передаються. Отже максимально можлива ентропія повідомлень
,
а пропускна здатність каналу
.
Приклад 10. Визначити необхідну пропускну здатність та смугу пропускання каналу, призначеною для передавання телевізійного зображення. Можна вважати, що телевізійне зображення складається із 600 000 дрібних елементів зображення. Кожний із цих елементів може приймати 10 різних градацій яскравості. Всі градації можна вважати рівномірними. За одну секунду передається 25 кадрів зображення. Крім того, відомо, що для задовільного відтворення зображення необхідне відношення сигнал/шум дорівнює 1000.
Розв’язання. Оскільки кожен елемент зображення може приймати 10 рівнів з рівною ймовірністю, то один елемент зображення містить кількість інформації
.
Один кадр містить
кількість інформації, яка дорівнює
біт.
Оскільки за одну секунду повинно бути
передано 25 кадрів, то пропускна здатність
каналу
.
Згідно з формулою Шенона пропускна здатність каналу зв’язку
.
Звідси можна
визначити смугу пропускання
:
.