- •5.1 Задание на расчетно-графическую работу № 5
- •5.2 Обозначения и краткие теоретические сведения
- •5.3 Расчеты по алгоритмам управления проектом
- •5.4 Рассчитаем ранние моменты наступления событий
- •5.5 Рассчитаем поздние моменты наступления событий
- •5.6 Рассчитаем резерв времени событий
- •5.7 Расчет фиктивных работ
- •Рассчитаем полный резерв времени на работы и определим критический путь
- •Рассчитаем свободный, независимый и гарантированный резервы времени
- •5.8 Анализ полученных результатов
5.1 Задание на расчетно-графическую работу № 5
Найти критический путь по алгоритмам управления проектом (СПУ), полный, свободный, независимый и гарантированный резервы времени. Продолжительности работ на рисунке 5.1 приведены в условных единицах.
2
4













6

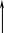

4
6
8
2
3
6



8










4





6
4
4
6
3
3
2
2
4
7
2












8
7
3






6
4
6
2
6
5
3










5





4
4
3
8
8
4





Рисунок
5.1
—
Сетевая модель проекта

5.2 Обозначения и краткие теоретические сведения
Введем
следующие обозначения:
![]() —
событие «Начало проекта»,
—
событие «Начало проекта»,
![]() —
событие
«Окончание проекта»,
—
событие
«Окончание проекта»,
![]() —
промежуточные
события проекта, фиксирующие начало и
окончание работы,
—
промежуточные
события проекта, фиксирующие начало и
окончание работы,
![]() — работа,
— работа,
![]() —
ранний
момент наступления события,
—
ранний
момент наступления события,
![]() —
поздний
момент наступления события.
—
поздний
момент наступления события.
Ниже, на рисунке 5.2, дана схема идентификации вершин графа — сети.



![]()
![]()
![]()
Рисунок
5.2—
Идентификация вершин графа—сети
В ведем
дополнительные обозначения:
ведем
дополнительные обозначения:
![]() —
формула для расчета раннего момента
наступления события,
—
формула для расчета раннего момента
наступления события,
![]() —
формула для расчета позднего момента
наступления события.
—
формула для расчета позднего момента
наступления события.
![]() —
резерв
времени события
,
т.е. максимальное время, на которое можно
задержать наступление события
без
задержки сроков завершения проекта.
—
резерв
времени события
,
т.е. максимальное время, на которое можно
задержать наступление события
без
задержки сроков завершения проекта.
Пример расчета ранних и поздних моментов наступления событий приведен на рисунках 5.3 и 5.4 соответственно.

Таким образом, полная схема идентификации вершин графа—сети показана на рисунке 5.5.



![]()
Рисунок 5.5 — Схема
идентификации вершин графа—сети
Равенство
![]() позднего
и раннего сроков наступления события
обозначает
ситуацию недопустимости задержки
наступления события
.
позднего
и раннего сроков наступления события
обозначает
ситуацию недопустимости задержки
наступления события
.
Введем следующие обозначения:
![]() —
полный
резерв времени
—
полный
резерв времени
работы
![]() .
.
Если![]() =
0, то работа
лежит на критическом пути (рисунок 5.6).
=
0, то работа
лежит на критическом пути (рисунок 5.6).
Ниже
приведены расчеты, поясняющие рисунок
5.6. Поскольку
![]() =
4 – 2 – 2 = 0,
=
4 – 2 – 2 = 0,
![]() =
8 – 2 – 4 =2,
=
8 – 2 – 4 =2,
![]() =
8 – 4 – 4 = 0, то работы 12 и 23 лежат на
критическом пути.
=
8 – 4 – 4 = 0, то работы 12 и 23 лежат на
критическом пути.
Введем следующие обозначения:
![]() —
свободный
резерв времени работы
,
—
свободный
резерв времени работы
,
![]() —
независимый
резерв времени работы
,
—
независимый
резерв времени работы
,
![]() —
гарантированный
резерв времени работы
.
—
гарантированный
резерв времени работы
.