Расчётные задания по материаловедению

КС-61-09

Гванцеладзе Александр Александрович

Расчет №1. Трансформатор-формирователь

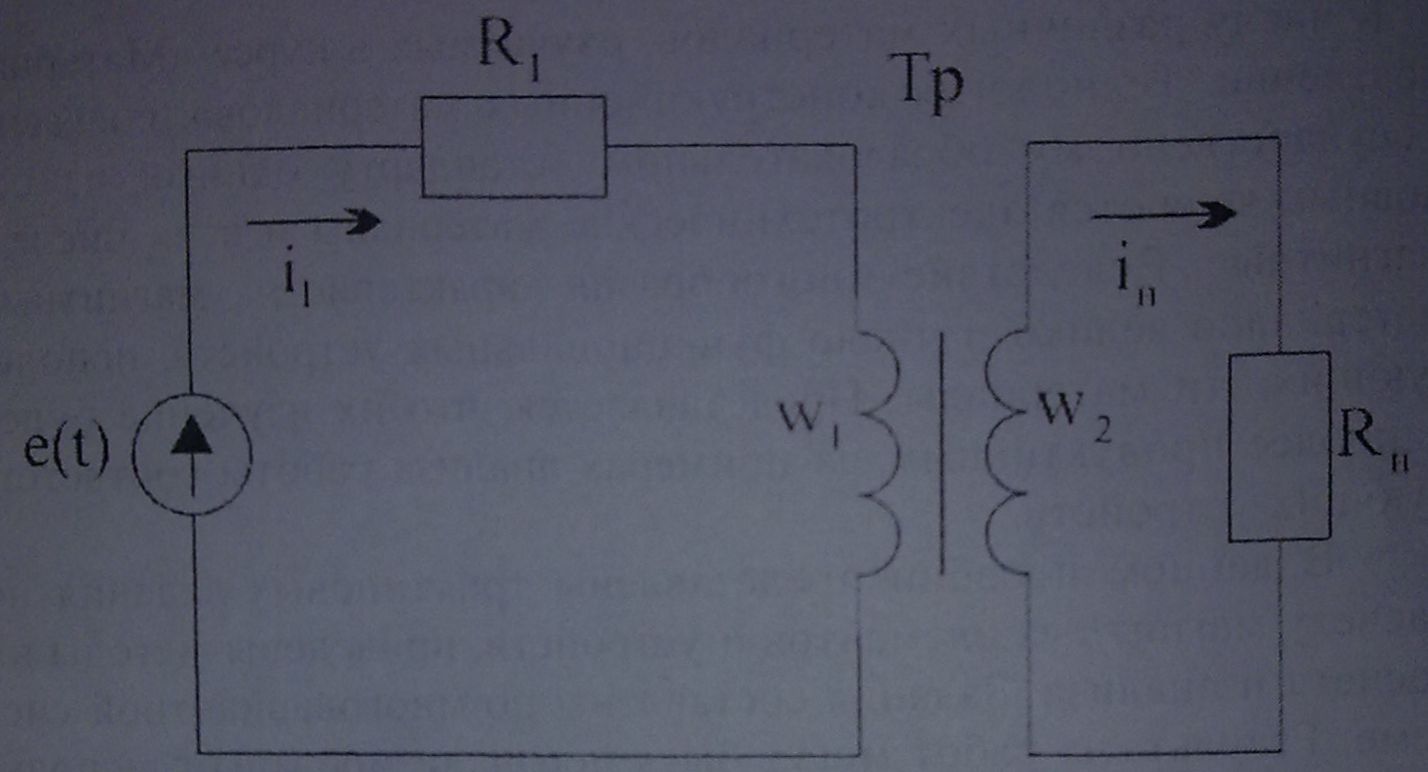
Рис. 2.1. Схема трансформатора-формирователя

Исходные данные:

1. Источник ЭДС e(t) - знакопеременное напряжение пря­моугольной формы с амплитудой Е и частотой f

2. R₁ - сопротивление резистора в первичной цепи.

3. R_Н - сопротивление резистора нагрузки.

4. Магнитопровод трансформатора - кольцевой сердечник с габаритными размерами D, d, h.

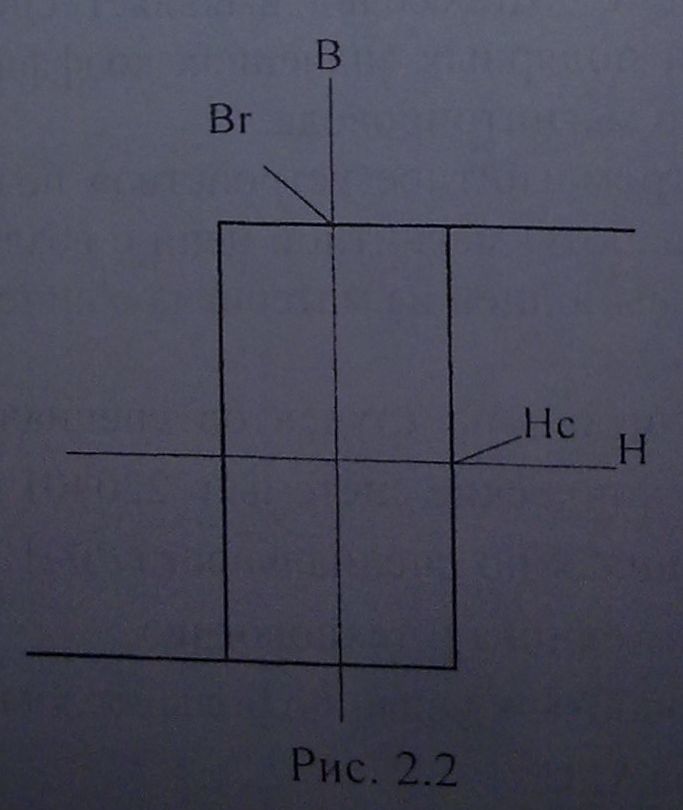
5. Магнитная характеристика сердечника представлена идеализированной зависимостью В(Н) с остаточной индукцией B_г и коэрцитивной силой Н_С(рис. 2.2).

6. W₁, W₂ - число витков первичной и вторичной обмоток трансформатора, соответственно.

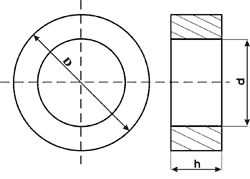
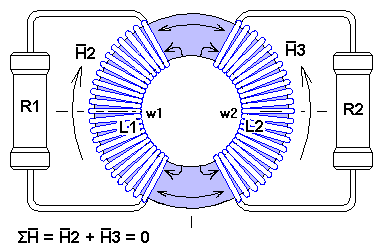
Примерная схема трансформатора.

2.1 Задание

Рассчитать и построить временные диаграммы тока в первичной цепи i₁(t), напряжение на нагрузке U_Н(t), а также изменения индукции В(t) и напряженности H(t) в магнитопроводе.

Определить значение амплитуды питающего напряжения E_Θ, при котором угол насыщения будет равен заданному значению Θ_S.

Таблица 2.1
№	Е	f	R1	Rн	W1	W2	Br	Нс	D	d	h
вар.	В	кГц	Ом	Ом			Тл	А/м	мм	мм	мм
10	3	2,5	40	100	50	50	0,3	75	10	5	1

2.2. Выполнение расчета.

Упростим расчетную схему, осуществив приведение сопротивления нагрузки к первичной обмотке:

R_н’=R_н•w₁²/w₂²=100•50²/50²=100 (Ом) (2-1)

Для схемы, представленной на рис. 2.3 для временного ин­тервала, соответствующего длительности полупериода питающе­го напряжения, составим систему уравнений, которую решим от­носительно напряжения на первичной обмотке U_W1.

По закону Кирхгофа для контура:

E=i₁•R₁+U_w1 (2-2)

По закону Кирхгофа для узла цепи:

i₁= i_н’₊ i_µ (2-3)

где i_µ намагничивающий ток (ток, потребляемый от источника ЭДС в режиме холостого хода);

Длина средней магнитной линии в l сердечнике равна:

l=(D+d)/2•π =(10+5)/2•π=23,56 (мм)

i_µ=H_c•l/w₁=75•23,56•10^-3/50=35,34•10^-3=35,34 (мА) (2-4)

приведенный ток нагрузки i_н’=U_w1/R_н’ (2-5)

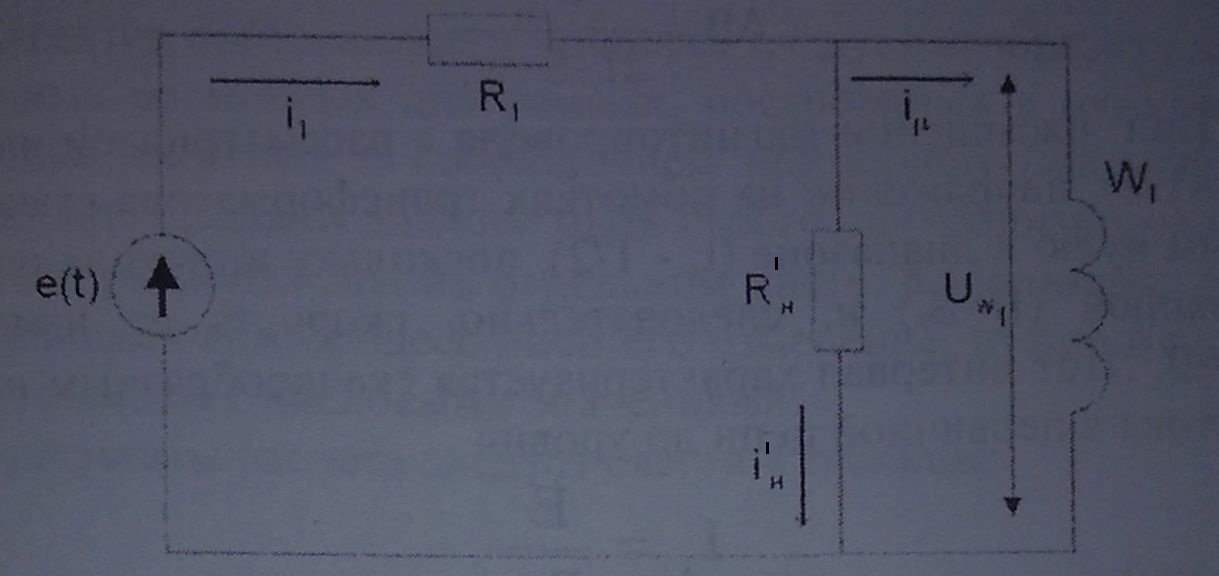
Рис. 2.3. Расчетная схема трансформатора

Решая систему уравнений, получим:

U_w1=[E-i_µ•R₁]/[1+R₁/R_н’]=(3-35,34•10^-3•40)/(1+40/100)=(3-1,414)/1,4=1,133 (В) (2-6)

i_н'=1,133/100=11,33 (мА)

i₁=11,33+35,34=46,67 (мА)

В соответствии с законом электромагнитной индукции:

U_w2=U_н=U_w1•w₂/w₁=1,133•50/50=1,133 (В) (2-7)

Постоянство во времени значения напряжения на обмотках трансформатора (U_W1 и U_W2) определяют линейный характер из­менения индукции B(t) на интервале от начала перемагничивания (В= -В_r) до его окончания (В= +В_r).

Площадь поперечного сечения S сердечника равна:

S=(D-d)/2•h=(10-5)/2•1=2,5 (мм²)

Время, за которое магнитопровод достигнет состояния на­сыщения t_s, определяется как

t_s=2•B_r•S•w₁/U_w1=2•0,3•2,5•50/1,133=66,20 мкс (2-8)

Если это время превышает длительность полупериода питающего напряжения

t_s>T/2=1/(2•f)=1/(2•f)=200 мкс (2-9)

то режима насыщения магнитопровода в пределах полупериода не наступает, а трансформатор работает в режиме, определяемом изменением индукции в сердечнике ΔВ<2В_r:

ΔB=U_w1/[2•f•S•w₁]=1,133/[2•2,5•10³•2,5•10^-6•50]=1,813 Тл (2-10)

При насыщении магнитопровода в рассматриваем интерва­ле (t_s<T/2), напряжение на обмотках трансформатора становится равным нулю в диапазоне (t_s-Т/2), поскольку индукция остается постоянной (В=В_r) и, следовательно, скорость ее изменения dB/dt=0. Этот интервал характеризуется скачкообразным измене­нием тока в первичной цепи до уровня

I_s=E/R₁=3/40=75 (мА) (2-11)

и, соответственно, напряженности в магнитопроводе до уровня

H_s=I_s•w₁/l=75•50/23,56=159,17 (А/м) (2-12)

Угол насыщения Θ_S может быть определен как

Θ_S=π•t_s/(T/2)=t_s•2•π/T=t_s•2•π•f=66,20•10^-6•2•π•2,5•10³=1,04 (радиан)≈59,8° (2-13)

При изменении знака питающего напряжения (четный полупериод) характер изменения переменных сохраняется, изменя­ется лишь их полярность. Задача определения амплитуды питающего напряжения E_S, соответствующей заданному углу на­сыщения Θ_s выполняется в обратном порядке.

Время перемагничивания t_S находим из соотношения (2-13)

t_s=Θ_s/[2•π•f]=1,04/(2•π•2,5•10³)=66,21 (мкс) (2-14)

Необходимые для этого значения напряжения на обмотках w₁, согласно соотношению (2-8)

U_w1=2•B_r•S•w/t_s=U_w2=U_н=2•0,3•2,5•50/66,21=1,133 (В) (2-15)

а амплитуду питающего напряжения в соответствии с (2-6)

E=U_w1•[1+R₁/R_н’]+i_µR₁=1,133•(1+40/100)+35,34•10^-3•40=1,5862+1,4136=3 (В) (2-16)

Характер протекающего процесса следует отобразить на со­вмещенных временных диаграммах, построенных в одинаковом временном масштабе с соблюдением примерного масштаба по оси ординат. Графики должны быть строго синхронизированы по времени и расположены на отдельном листе. Координаты точек, определяющих сам процесс либо его изменение, нужно отметить на диаграммах их числовыми значениями.

Результаты расчета:

Таблица 2.2
№ вар-та	l, мм	S, мм2	Rн', Ом	Т/2,мкс	Iµ, мА	ts, мкс
10	23,56	2,5	100	200	35,34	66,20

Таблица 2.3
Для t≤ts
Uw1,B	I1,мA	Uн,B
1,133	46,67	1,133

Таблица 2.4
Для t>ts
Uw1,B	I1,мA	Uн,B
1,133	75	0