- •Затверджено
- •Contents Contents
- •The purpose and the contents of laboratory works
- •Laboratory work №1 Solution of Nonlinear Equations by the Bisection method and Chord method
- •1.1 Purpose of the work
- •1.2 Tasks for laboratory work
- •1.3 The basic theoretical knowledge
- •1.3.1 Bisection method
- •Figure 1.1 – Bisection method
- •Chord method
- •Figure 1.4 – Chord method
- •1.3.3 Matlab function fzero and roots
- •1.4 Individual tasks
- •1.5 Control questions
- •Laboratory work №2 Solution of Nonlinear Equations by the newton method and simple iteratIvE method
- •Figure 2.1 – Newton method
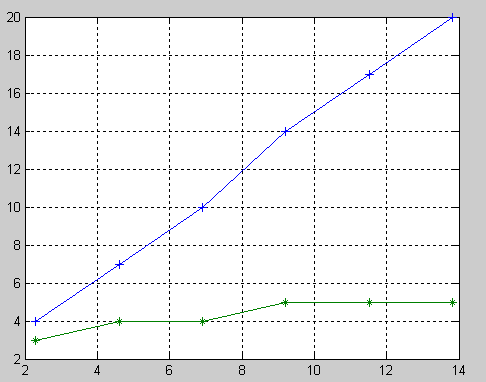
- •Figire 2.2 - Dependence of the number of iterations on the accuracy of methods for the bisection (upper line) and the Newton method (bottom line)
- •2.3.2 The method of simple iteration
- •A sufficient condition for the convergence of the iterative process
- •Individual tasks
- •Laboratory work №3 Solution system of Linear Algebraic Equations
- •3.3.1 Direct methods
- •Inverse matrix:
- •3.3.2 Iterative methods
- •Condition number of a
- •3.4 Individual tasks
- •3.5 Control questions
- •Laboratory work №4
- •Visualization of 3d data in matlab
- •Plot3(X, y, z, 'style')
- •4.3.2 Instructions: meshgrid, plot3, meshc, surfc
- •4.3.3 Instructions: sphere, plot3, mesh
- •4.3.4 The simple animation in 3d
- •1. Working with a sphere
- •4.3.5 Summary of 3d Graphics
- •Individual tasks
- •Laboratory work №5 Solving systems of nonlinear equations
- •5.1 Purpose of the work
- •5.2 Tasks for laboratory work
- •5.3 The basic theoretical knowledge
- •5.3.1 Newton method to solve systems of non-linear equations
- •5.3.2 Matlab function for Newton method for a system of nonlinear equations
- •5.3.3 The matlab routine function fsolve
- •Input Arguments
- •Individual tasks
- •5.5 Control questions
- •List of the literature
- •Appendix a.
- •Individual tasks to Lab number 1, 2
- •Appendex b. The task for self-examination to Lab number 1, 2
Figure 2.1 – Newton method
The programming algorithm of any of iterative methods must include the option of stopping the program if the number of iterations grows too large. How large is large? That will depend of the particular problem solved. However, any Newton, or other method solution that takes more than 1000 iterations to converge is either ill-posed or contains a logical error. Debugging of the program will be called for at this point by changing the initial values provided to the program, or by checking the program's logic.
Program of Newton method is shown in listing 2.1.
Listing 2.1. File newton.m
function [x,k]=newton(fname,fname1,x0,eps)
%fname– name m-file containing a description of the functions included in % nonlinear equation f(x)=0;
%fname1– name m.file containing description of the first derivative of the % function f(x);
% x0 - initial approximation;
% eps – accuracy
% k – number of iterations;
% x – root;
%.
k=0;
f=feval(fname,x0); f1= feval(fname1,x0);
x1=x0-f/f1;
while abs(x0-x1)>eps & k < 100
x0=x1;
f=feval(fname,x0);
f1= feval(fname1,x0);
x1=x0-f/f1;
k=k+1;
end;
x=x1;
Example 2.1. Find the root of the equation
cos(x) = x3
using the method of tangent.
We can rephrase that as finding the zero of f(x) = cos(x) − x3. We have f '(x) = −sin(x) − 3x2. Since cos(x) ≤ 1 for all x and x3 > 1 for x>1, we know that our zero lies between 0 and 1. We try a starting value of x0 = 0.5.
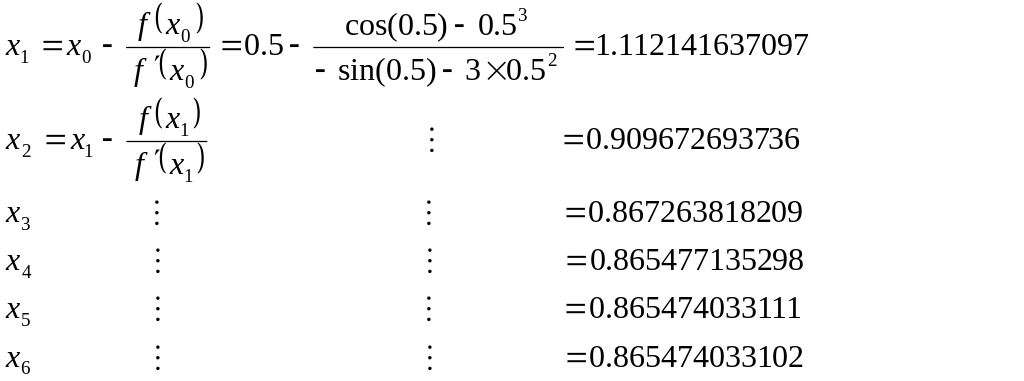
Thus the six iterations, the resulting root with an accuracy ε = |0.86547403311-0.865474033102|=0.000000000009
Example
2.2. Find
the root of the equation f(x)=0,
where
![]() using
the methods of tangent and besection.
using
the methods of tangent and besection.
Compare methods for the convergence rate and volume calculations.
1. Create a file var1.m(listing 2.2), containing a description of the function
listing 2.2. File var1.m
function z=var1(x)
z=3*x.^4+4*x.^3-12*x.^2-5;
2. Create a file var11.m(listing 2.3), containing a first derivative
listing 2.3. File var11.m
function y=var11(x)
y=12*x.^3+12*x.^2-24*x;
3. Script(listing 2.4) builds a graph of the number of iterations required to calculate the root with given accuracy of the Newton method and bisection
listing 2.4. File test.m
x1=zeros(1,6); k1=zeros(1,6); x2=zeros(1,6); k2=zeros(1,6);
eps=[0.1, 0.01, 0.001, 0.0001, 0.00001, 0.000001];
for i=1:6
[x1(i),k1(i)]=Bisec(@var1,-3,-2,eps(i));
[x2(i),k2(i)]=newton(@var1,@var11,-2.5,eps(i));
end;
disp(x1,x2)
plot(log(1./eps),k1,'k-.',log(1./eps),k2,'k:')
grid on
The result of the function test shown in on the figure 2.2. On the axis 0x plotted the natural logarithms of the inverse of the accuracy (with increasing accuracy increases and the argument on the axis 0x). On the axis 0Y - the number of iterations needed to calculate the root with a given accuracy. <br>It is seen that with increasing the accuracy of the Newton method requires far fewer iterations, however, at each iteration, one value function and a single value of the derivative, whereas in the method of bisection at each iteration, only one function value. As stated in the theorem, Newton’s method has local convergence, ie, its area of convergence is a small neighborhood of the root. Poor choices can give divergent iterative sequence.