1.4 Individual tasks

Variants of the tasks are presented in the Appendix A (p.77).

1. Found a roots of the given equations if accuracy is less than  = 10^-4. Use:

a) Bisection method;

b) Chord method;

2. Locate one of the roots with several relative errors. Compare the amount of calculations using these methods for different errors.

3. Along with the "manual" solution provide solutions obtained by standard means of MatLab (functions fzero and root).

1.5 Control questions

1. Stages of the decision of the nonlinear equations.

2. Cut-and-try method. Illustrate on the graph. Merits and demerits of a method.

3. The method of hords. Illustrate on the graph. Merits and demerits of a method.

4. The method of simple iteration. Illustrate on the graph. Merits and demerits of a method.

5. The method of tangents (Newton’s method). Illustrate on the graph. Merits and demerits of a method.

6. Solving Nonlinear Equation in MATLAB –functions roots and fzero.

Laboratory work №2 Solution of Nonlinear Equations by the newton method and simple iteratIvE method

2.1 Purpose of the work

This laboratory work helps students a)study of Newton and Simple Iterative methods for solving nonlinear equations; b) the use of MATLAB for solving nonlinear equations.

2.2 Tasks for laboratory work

1. To study the iterative methods(Newton and Chord) for solving nonlinear equations

2. Make a programs-functions to find the root of the Newton and Simple Iteration methods.

3. To carry out the individual task.

4. Save results of the work (the programs, listing of calculation) at your personal files.

5. Draw up report.

2.3 The basic theoretical knowledge

2.3.1 The method of tangent(Newton)

Consider the Taylor-series expansion of the function f(x) about a value x = xo:

f(x)= f(xo)+f'(xo)(x-xo)+(f"(xo)/2!)(x-xo)2+….

Using only the first two terms of the expansion, a first approximation to the root of the equation

f(x) = 0

can be obtained from

f(x) = 0 ≈ f(xo)+f'(xo)(x1 -xo)

Such approximation is given by,

x1 = xo - f(xo)/f'(xo).

The Newton method consists in obtaining improved values of the approximate root through the recurrent application of equation above. For example, the second and third approximations to that root will be given by

x2 = x1 - f(x1)/f'(x1),

and

x3= x2 - f(x2)/f'(x2),

respectively.

This iterative procedure can be generalized by writing the following equation, where i represents the iteration number:

x_i+1 = x_i - f(x_i)/f'(x_i).

After each iteration the program should check to see if the convergence condition, namely,

|f(x _i+1)|<ε

or

|xi+1 – x i| ≤ ε,

is satisfied.

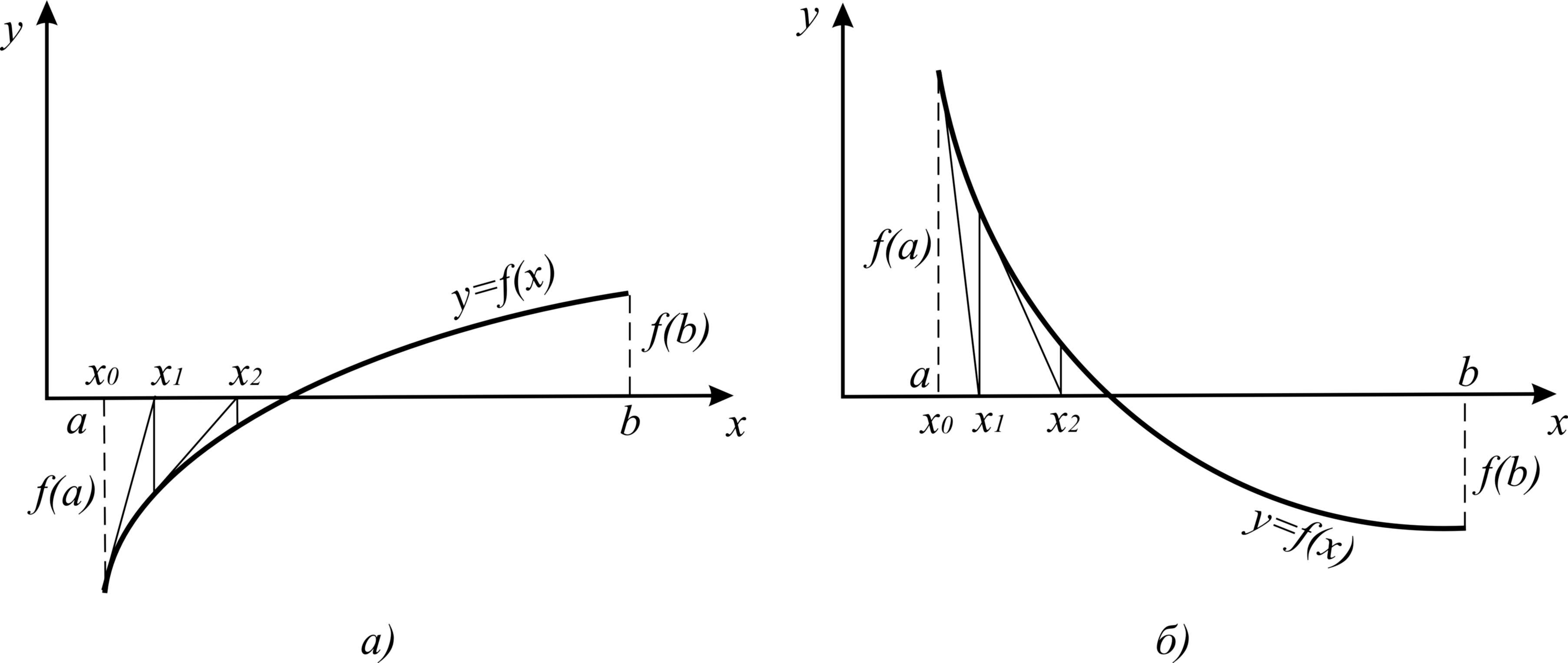
The figure below(picture 2.1) illustrates the way in which the solution is found by using the Newton method. Notice that the equation

f(x) = 0 ≈ f(xo)+f'(xo)(x1 -xo)

represents a straight line tangent to the curve y = f(x) at x = xo. This line intersects the x-axis (i.e., y =f(x) = 0) at the point xi as given by xi = xo - f(xo)/f'(xo). At that point we can construct another straight line tangent to y = f(x) whose intersection with the x-axis is the new approximation to the root of f(x) = 0, namely, x = x2. Proceeding with the iteration we can see that the intersection of consecutive tangent lines with the x-axis approaches the actual root relatively fast.

The Newton method converges relatively fast for most functions regardless of the initial value chosen. The main disadvantage is that you need to know not only the function f(x), but also its derivative, f'(x), in order to achieve a solution.