Laboratory work №5 Solving systems of nonlinear equations

5.1 Purpose of the work

This lab will help students acquire the knowledge necessary for solving systems of nonlinear equations in Matlab.

5.2 Tasks for laboratory work

1. To study the iterative method (Newton) for solving system of nonlinear equations.

2. Make a programs-functions to find the roots of the Newton method.

3. To carry out the individual task.

4. Save results of the work (the programs, listing of calculation) at your personal files.

5. Draw up report.

5.3 The basic theoretical knowledge

Consider the solution to a system of n non-linear equations in n unknowns given by

The system can be written in a single expression using vectors, i.e.,

F(x)=0,

where the vector x contains the independent variables, and the vector F contains the functions f_i(x):

х = ; F(x) = .

We will look at one method in particular, Newton's method. We are going to write our own routine function for solving non-linear equations using Newton's method. Matlab has its own routines for solving systems of nonlinear equations (e.g. fsolve, which is loosely based on Newton's method). Look up the routines fsolve in the Matlab help file

5.3.1 Newton method to solve systems of non-linear equations

A Newton method for solving the system of linear equations requires the evaluation of a matrix, known as the Jacobian of the system, which is defined as:

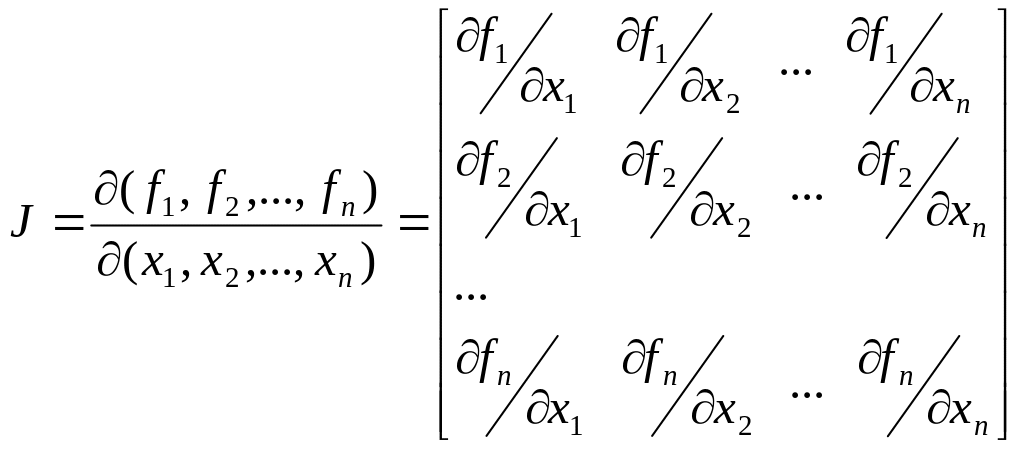
If x = x⁰ (a vector) represents the first guess for the solution, successive approximations to the solution are obtained from

A convergence criterion for the solution of a system of non-linear equation could be, for example, that the maximum of the absolute values of the functions f_i(x⁽ⁿ⁾) is smaller than a certain tolerance ε, i.e.,

.

We can also use as convergence criteria the difference between consecutive values of the solution, i.e.,

.

Example 5.1. To illustrate the solving system of non-linear equations:

we start by defining an initial guess for the solution as .

Then:

F(x⁽⁰⁾)=(-0.25, -1.25, -1.0).

;

;

.

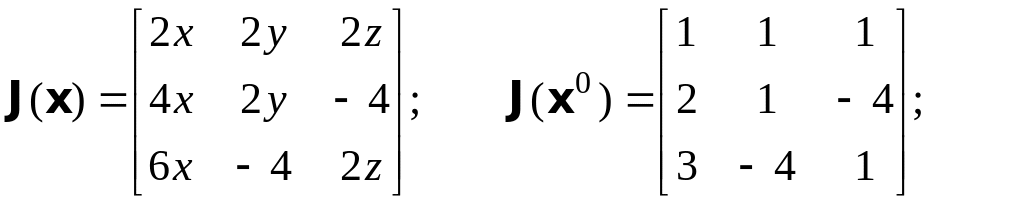
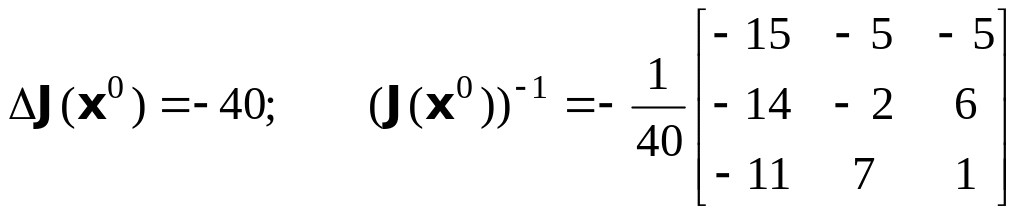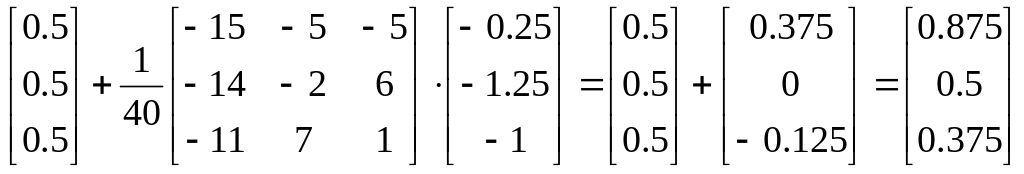5.3.2 Matlab function for Newton method for a system of nonlinear equations

The following MATLAB function, newtonm, calculates the solution to a system of n nonlinear equations, f(x) = 0, given the vector of functions f and the Jacobian J, as well as an initial guess for the solution x⁰.

function [x,iter] = newtonm(x0,f,J,maxiter,epsilon)

% Newton method applied to a

% system of linear equations f(x) = 0,

% given the jacobian function J, with

% x = [x₁;x₂;...;x_n], f = [f₁;f₂;...;f_n]

% x0 is an initial guess of the solution

% maxiter - max. number of iterations

% epsilon – tolerance

xx = x0; % load initial guess

for iter=1: maxiter

JJ = feval(J,xx);

if abs(det(JJ))<epsilon

error('newtonm - Jacobian is singular - try new x0');

abort;

end;

xn = xx - inv(JJ)*feval(f,xx);

if (abs(feval(f,xn))<epsilon )|(norm(xx-xn)<epsilon)

x=xn;

return;

end;

xx = xn;

end;

error('No convergence after maxiter iterations.');

abort;

% end function

Solution using function newtonm

Next, we use function newtonm to solve the problem postulated earlier. The functions f and the Jacobian J need to be defined as separate functions.

We can define the function f as the following user-defined MATLAB function fun:

function [y]=fun(x)

% fun(x) = 0, with x = [x(1);x(2),x(3)]

% represents a system of 3 non-linear equations

y=[x(1)^2+x(2)^2+x(3)^2-1;

2*x(1)^2+x(2)^2-4*x(3);

3*x(1)^2-4*x(2)+x(3)^2];

%end function

The corresponding Jacobian is calculated using the user-defined MATLAB function funJacob:

function [w]=funJacob(x)

% Evaluates the Jacobian of a 3x3

% system of non-linear equations

w(1,1)=2*x(1); w(1,2)=2*x(2); w(1,3)=2*x(3);

w(2,1)=4*x(1); w(2,2)=2*x(2); w(2,3)=-4;

w(3,1)=6*x(1); w(3,2)=-4; w(3,3)=2*x(3);

%end function

Next, we use function newtonm to solve the problem postulated earlier.

A call to the function using the values of x0, fun, funJacob, mxiter and tolerance is:

>> x=[0.5;0.5;0.5];

>> maxiter=30; eps=1e-6;

>> [x,iter] = newtonm(x0,'fun','funJacob',maxiter,eps)

x =

0.7852

0.4966

0.3699

iter =

4

The result shows the number of iterations required for convergence and the solution found as x1== 0.7852, x2 = 0.4966 and x3=0.3699.