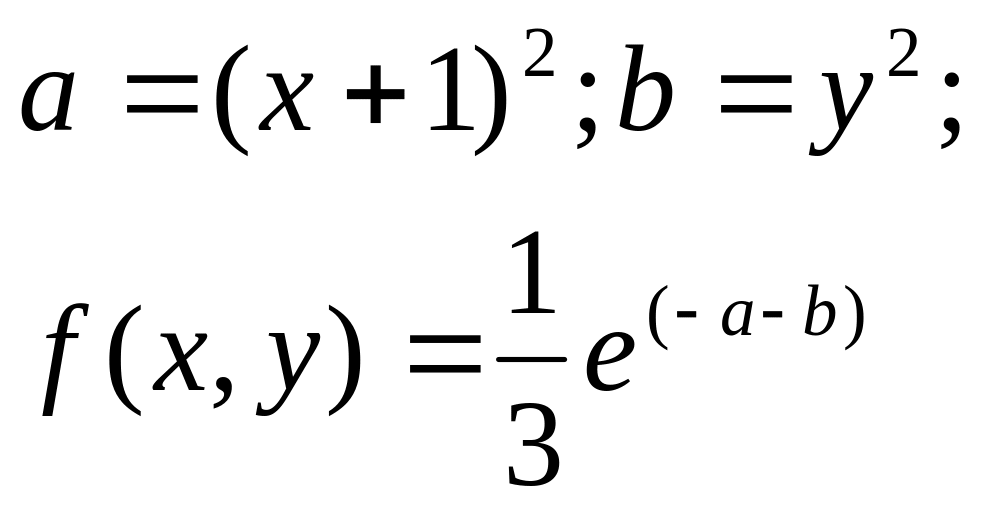- •Затверджено
- •Contents Contents
- •The purpose and the contents of laboratory works
- •Laboratory work №1 Solution of Nonlinear Equations by the Bisection method and Chord method
- •1.1 Purpose of the work
- •1.2 Tasks for laboratory work
- •1.3 The basic theoretical knowledge
- •1.3.1 Bisection method
- •Figure 1.1 – Bisection method
- •Chord method
- •Figure 1.4 – Chord method
- •1.3.3 Matlab function fzero and roots
- •1.4 Individual tasks
- •1.5 Control questions
- •Laboratory work №2 Solution of Nonlinear Equations by the newton method and simple iteratIvE method
- •Figure 2.1 – Newton method
- •Figire 2.2 - Dependence of the number of iterations on the accuracy of methods for the bisection (upper line) and the Newton method (bottom line)
- •2.3.2 The method of simple iteration
- •A sufficient condition for the convergence of the iterative process
- •Individual tasks
- •Laboratory work №3 Solution system of Linear Algebraic Equations
- •3.3.1 Direct methods
- •Inverse matrix:
- •3.3.2 Iterative methods
- •Condition number of a
- •3.4 Individual tasks
- •3.5 Control questions
- •Laboratory work №4
- •Visualization of 3d data in matlab
- •Plot3(X, y, z, 'style')
- •4.3.2 Instructions: meshgrid, plot3, meshc, surfc
- •4.3.3 Instructions: sphere, plot3, mesh
- •4.3.4 The simple animation in 3d
- •1. Working with a sphere
- •4.3.5 Summary of 3d Graphics
- •Individual tasks
- •Laboratory work №5 Solving systems of nonlinear equations
- •5.1 Purpose of the work
- •5.2 Tasks for laboratory work
- •5.3 The basic theoretical knowledge
- •5.3.1 Newton method to solve systems of non-linear equations
- •5.3.2 Matlab function for Newton method for a system of nonlinear equations
- •5.3.3 The matlab routine function fsolve
- •Input Arguments
- •Individual tasks
- •5.5 Control questions
- •List of the literature
- •Appendix a.
- •Individual tasks to Lab number 1, 2
- •Appendex b. The task for self-examination to Lab number 1, 2
4.3.5 Summary of 3d Graphics
Three-dimensional plots (or 3D graphs) can be created by this numerical software.
Matlab provides many facilities for visualization of 3D information or data (x, y, z). The facilities include built-in functions for plotting wire-frame objects, space-curves, shaded surfaces.
Also, automatic generation of contours, volumetric data display, light sources, interpolation of colors and displaying externally-created images.
Typing ‘help graph3d’ in the command window gives a list of functions available for general 3D graphs.
This is a kind of ‘catalog’ of the most popular 3D graphics functions.
You can use these instructions for your needs simply by following the examples. The ‘meshgrid’ function must be first understood.
Examples:
plot3
|
t = 0 : .01 : 1; x = 2*t; y = -0.5*t.^2; z1 = t.^3/2; z2 = t.^3/.5; plot3(x,y,z1,'b', x,y,z2,'r') grid
|
fill3 |
x = [0 2.5; 5 2.5; 5 2.5; 0 2.5]; y = [0 0; 0 -1; 0 -1; 0 0]; z = [0 0; 0 0; 2 2; 2 2]; fill3(x,y,z, rand(4,2)) xlabel('x'); ylabel('y'); zlabel('z'); view(120, 50) grid
|
contour3
|
X = -3:.1:3; [x,y] = meshgrid(X,X); z = 1./(3+x.^2+y.^2); contour3(z) xlabel('x'); ylabel('y');
|
surf
|
X = -3 : .1 : 3; [x,y] = meshgrid(X,X); z = 1./(3+x.^2+y.^2); surf(z) xlabel('x'); ylabel('y');
|
surfc
|
X = -3 : .1 : 3; [x,y] = meshgrid(X,X); z = 1./(3+x.^2+y.^2); surfc(z) view(-30,20) xlabel('x'); ylabel('y');
|
surfl |
X = -3 : .1 : 3; [x,y] = meshgrid(X,X); z = 1./(3+x.^2+y.^2); surfl(z) shading interp colormap hot xlabel('x'); ylabel('y');
|
mesh |
X = -2 : .1 : 2; [x,y] = meshgrid(X,X); z = 5./(1+x.^2+y.^2); mesh(z) xlabel('x'); ylabel('y');
|
waterfall |
X = -3 : .1 : 3; [x,y] = meshgrid(X,X); z = -1./(1+x.^2+y.^2); waterfall(z) hidden off xlabel('x'); ylabel('y');
|
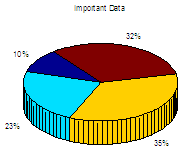
pie3 |
data = [10 23 35 32];
pie3(data)
title('Important Data')
|
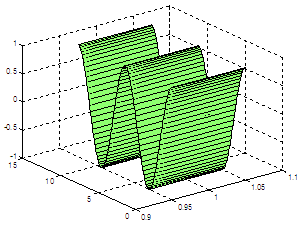
ribbon |
x = 0 : .1 : 4*pi;
y = cos(x);
ribbon(x,y,.1)
|
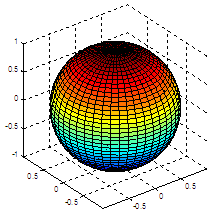
sphere |
sphere(45) axis 'equal'
|
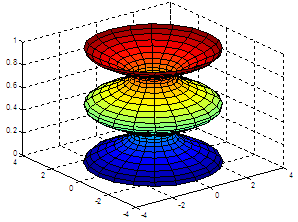
cylinder |
z = 0: .03 : 1; r = cos(4*pi*z)+2; cylinder(r)
|
Individual tasks
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
21 |
, -2.1 ≤ x ≤ 2.1 and -6 ≤ y ≤ 6 |
22 |
|