- •Затверджено
- •Contents Contents
- •The purpose and the contents of laboratory works
- •Laboratory work №1 Solution of Nonlinear Equations by the Bisection method and Chord method
- •1.1 Purpose of the work
- •1.2 Tasks for laboratory work
- •1.3 The basic theoretical knowledge
- •1.3.1 Bisection method
- •Figure 1.1 – Bisection method
- •Chord method
- •Figure 1.4 – Chord method
- •1.3.3 Matlab function fzero and roots
- •1.4 Individual tasks
- •1.5 Control questions
- •Laboratory work №2 Solution of Nonlinear Equations by the newton method and simple iteratIvE method
- •Figure 2.1 – Newton method
- •Figire 2.2 - Dependence of the number of iterations on the accuracy of methods for the bisection (upper line) and the Newton method (bottom line)
- •2.3.2 The method of simple iteration
- •A sufficient condition for the convergence of the iterative process
- •Individual tasks
- •Laboratory work №3 Solution system of Linear Algebraic Equations
- •3.3.1 Direct methods
- •Inverse matrix:
- •3.3.2 Iterative methods
- •Condition number of a
- •3.4 Individual tasks
- •3.5 Control questions
- •Laboratory work №4
- •Visualization of 3d data in matlab
- •Plot3(X, y, z, 'style')
- •4.3.2 Instructions: meshgrid, plot3, meshc, surfc
- •4.3.3 Instructions: sphere, plot3, mesh
- •4.3.4 The simple animation in 3d
- •1. Working with a sphere
- •4.3.5 Summary of 3d Graphics
- •Individual tasks
- •Laboratory work №5 Solving systems of nonlinear equations
- •5.1 Purpose of the work
- •5.2 Tasks for laboratory work
- •5.3 The basic theoretical knowledge
- •5.3.1 Newton method to solve systems of non-linear equations
- •5.3.2 Matlab function for Newton method for a system of nonlinear equations
- •5.3.3 The matlab routine function fsolve
- •Input Arguments
- •Individual tasks
- •5.5 Control questions
- •List of the literature
- •Appendix a.
- •Individual tasks to Lab number 1, 2
- •Appendex b. The task for self-examination to Lab number 1, 2
3.5 Control questions
What is the solution of the system of equations?
When the solution to Ax = b exists and is unique?
What are the direct methods for solving systems you know?
Solving systems of equations with MATLAB by direct methods.
What are the iterative methods for solving systems you know?
Give an algorithm for Jacobi.
Give an algorithm for Seidel.
What is ill-conditioned system of equations? Formulate a definition of the condition number matrix A? How can calculate condition number in MatLab?
Formulate a sufficient condition for convergence of iterative methods (Jacobi and Seidel).
Formulate criteria for the completion of the iterative process in the methods of Jacobi and Seidel.
Laboratory work №4
Visualization of 3d data in matlab
4.1 Purpose of the work
To study a few of the most important graphics functions and practical skills gaining of their use in the MatLab
4.2 Tasks for laboratory work
1. Study item 4.3.
2. Repeat all examples adduced in item 4.3.
3. Carry out in MatLab the individual task - item 4.4.
4. Save the result of the work (protocol of the work, graphics) in your personal folder.
5. Draw up report.
4.3 The basic theoretical knowledge
4.3.1 Instructions: view, grid, subplot
Matlab provides many powerful instructions for the visualization of 3D data. The instructions provided include tools to plot wire-frame objects, 3D plots, curves, surfaces. and can automatically generate contours, display volumetric data, interpolate shading colors and even display non-Matlab made images. Here are some commonly used functions (there are many more):
plot3, stem3, pie3, comet3, contour3, mesh, meshc,
surf, surfc, sphere, ellipsoid, cylinder.
Among these instructions, plot3 and comet3 are the 3D matches of plot and comet commands mentioned in the 2D plot section.
Function plot3
The general syntax for the plot3 command is
Plot3(X, y, z, 'style')
This command draws a 3D curve with the specified line style. The argument list can be repeated to make overlay plots, just the same way as with the plot command in 2D.
We have to make some necessary comments before any example can be introduced.
Plots in 3D may be annotated with instructions already mentioned for 2D plots: xlabel, ylabel, title, legend, grid, etc., plus the addition of zlabel. The grid command in 3D makes the appearance of the plots better, especially for curves in space.
Function view
The viewing angle of the observer is specified by the command view(azimuth, elevation), where
azimuth (in degrees): specifies the horizontal rotation from the y-axis, measured positive counterclockwise (default value is -37.5 degrees).
elevation (in degrees): specifies the vertical angle measured positive above the xy-plane (default value is 30 degrees).
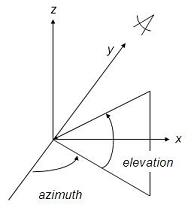
Figure 4.1 - Rotates the figure to azimuth=37.5 degrees, elevation=30 degrees
By specifying appropriate values of azimuth and elevation, one can plot projections of 3D objects on different 2D planes. For example, the command 'view(90,0)' places the viewer toward the positive x-axis, looking straigth on the yz-plane, and thus produces a 2D projection of the object on the yz-plane. 'view(0, 90)' shows the figure on a 2D xy-plane.
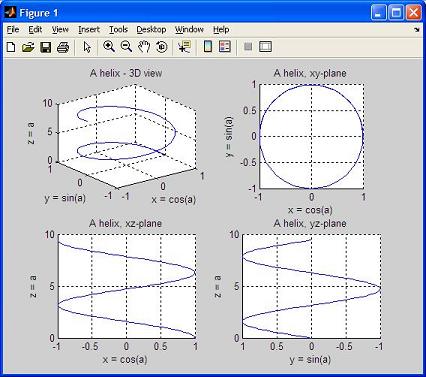
The following script generates data, plots the curves and obtains different views.
Example 1:
% clears variables, command window and closes all previous figures
clear; clc; close all
% generates an angle vector with 101 values
a = 0: 3*pi/100 : 3*pi;
% calculates x, y, and z
x = cos(a);
y = sin(a);
z = a;
% divides the figure window into 4 subwindows (2x2)
% plots on the 1st. one
subplot(2,2,1)
plot3(x,y,z)
grid on
title('A helix - 3D view')
xlabel('x = cos(a)')
ylabel('y = sin(a)')
zlabel('z = a')
% plots on the 2nd. subwindow
subplot(2,2,2)
plot3(x,y,z)
axis('square')
% rotates the figure to show only the xy-plane
view(0,90)
grid on
title('A helix, xy-plane')
xlabel('x = cos(a)')
ylabel('y = sin(a)')
zlabel('z = a')
% plots on the 3rd. subwindow
subplot(2,2,3)
plot3(x,y,z)
% rotates the figure to show only the xz-plane
view(0,0)
grid on
title('A helix, xz-plane')
xlabel('x = cos(a)')
ylabel('y = sin(a)')
zlabel('z = a')
% plots on the 4th. subwindow
subplot(2,2,4)
plot3(x,y,z)
% rotates the figure to show only the yz-plane
view(-90,0)
grid on
title('A helix, yz-plane')
xlabel('x = cos(a)')
ylabel('y = sin(a)')
zlabel('z = a')
And the result is: