ОПТИКА

Основные понятия и определения.

Свет – электромагнитная волна.

Классическая электродинамика рассматривает свет как электромагнитные волны. В случае плоской волны колебания напряженности электрического поля записываются в виде:

.

Волна распространяется в направлении волнового вектора и проходит через точку наблюдения, заданную радиус вектором .

Из уравнений Максвелла для плоской волны в однородной непроводящей среде следуют равенства

,

где - индукции электрического и магнитного полей.

Первые два равенства показывают, что волна поперечна для полей и .

Вторые два равенства показывают, что векторы электрического и магнитного полей взаимно перпендикулярны , причем образуют правовинтовую тройку векторов. Кроме того, следует, что E(t) и H(t) в любой момент времени связаны соотношением

или .

Н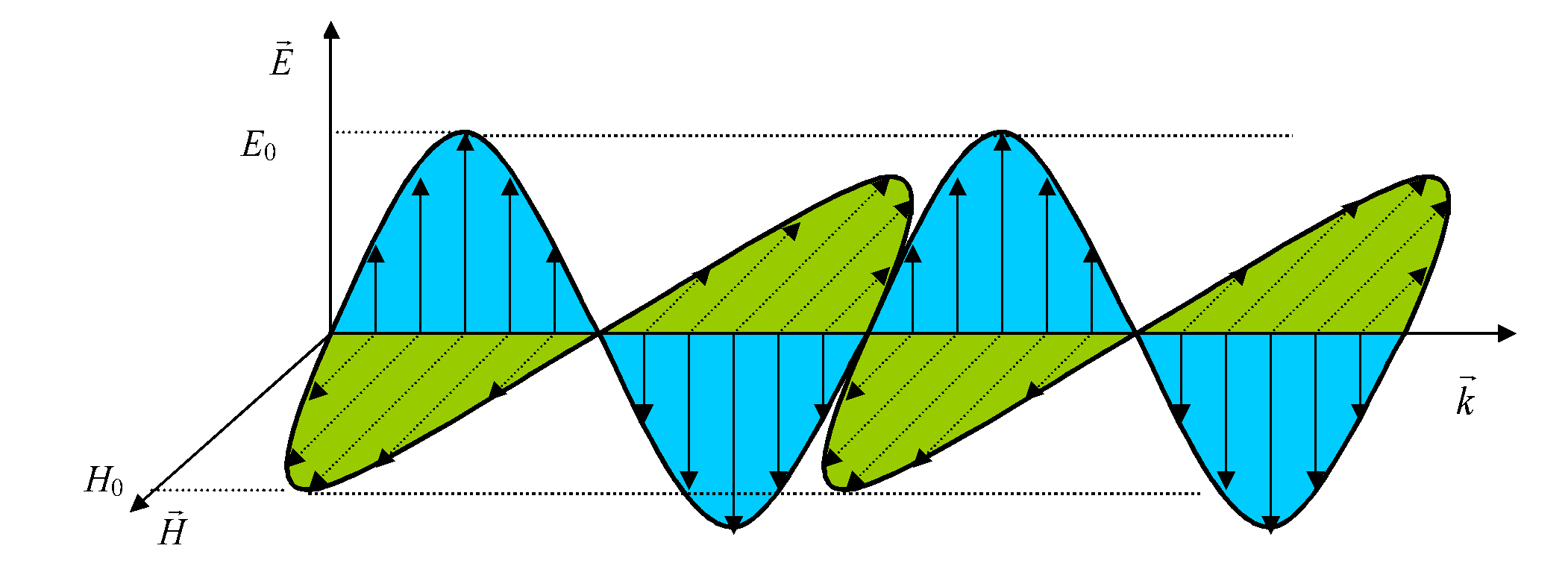 апряженность Е и Н одновременно достигают амплитудных значений E_m и H_m и одновременно обращаются в ноль (синфазность колебаний, см. рис.).

Фазовая скорость волны , где - показатель преломления оптической среды, ,  - диэлектрическая и магнитная проницаемости, - скорость света в вакууме. Для немагнитных сред  = 1 и .

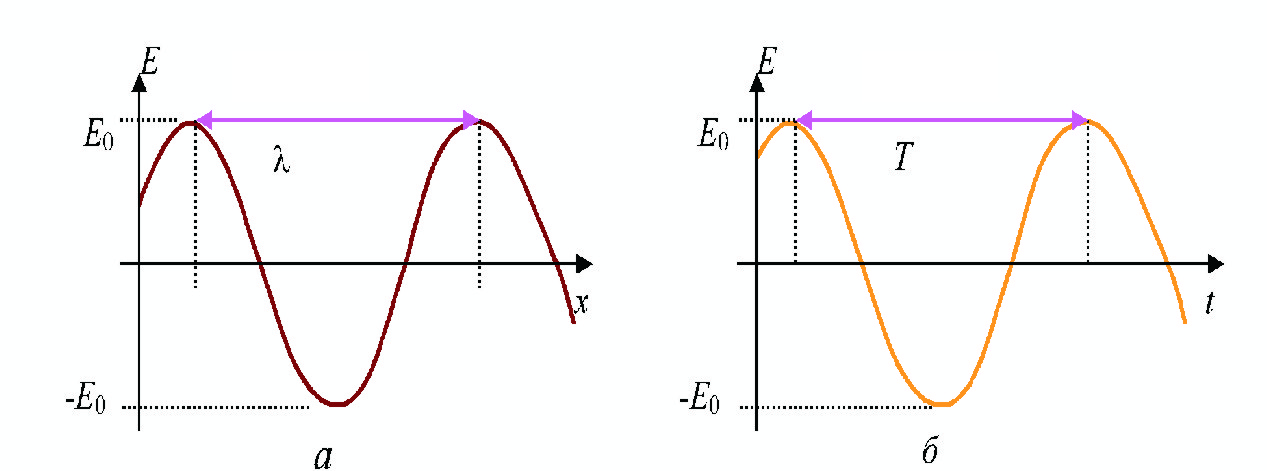Если зафиксировать момент времени, то получаем синусоидальное распределение поля Е в пространстве (вдоль оси х) в данный момент времени (см рис. а). Если зафиксируем значение координаты х, то получим синусоидальное распределение поля Е в зависимости от времени (см рис. б)- гармонические колебания с частотой .

Частота , где Т – период колебаний (для света ).

Волновое число (модуль вектора ), где - длина волны в вакууме (расстояние, проходимое волной за время одного периода). Длина волны в среде .

Таким образом, колебания и в световой волне происходят по закону

,

где  - фаза колебаний, ₀ – начальная фаза.

Отметим, что в сферической волне (от точечного источника) фаза .

Плотность потока энергии (вектор Пойнтинга) в волне:

,

где - единичный вектор в направлении распространения.

Интенсивность I световой волны - среднее по времени значение модуля вектора Пойнтинга:

,Вт/м², где - среднее значение плотности энергии электромагнитных колебаний. Интенсивность пропорциональна квадрату амплитуды колебаний .

Поток энергии dФ через площадку dS определяется как dФ = IdS_, Вт, где ,  - угол между вектором и нормалью к площадке dS.

Поляризация электромагнитной волны

Состояние поляризации определяют по проекционной картине – по типу траектории конца вектора (напряженности электрического поля) в проекции на плоскость, перпендикулярную направлению распространения при наблюдении навстречу волне.

Пусть волна распространяется в направлении оси x. Колебания вектора в волне могут быть представлены как сумма взаимно перпендикулярных колебаний:

,

где - разность фаз.

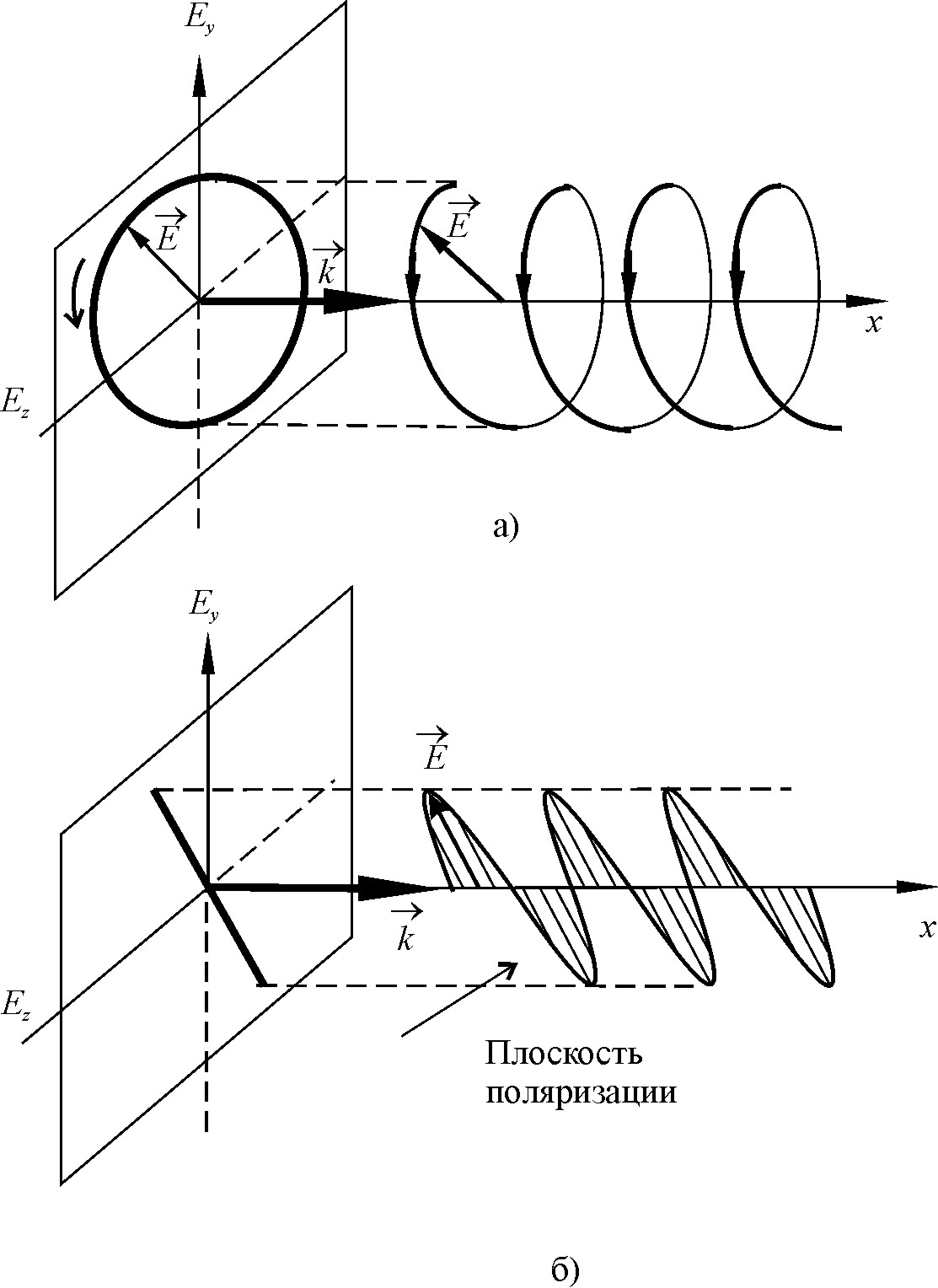
Электромагнитная волна одной частоты в общем случае имеет эллиптическую поляризацию.

(1)

Ориентация эллипса и его параметры зависят от соотношения между амплитудами колебаний a₁ и a₂ и от разности фаз . Если в формуле (1) , то эллипс поляризации превращается в окружность - круговая поляризация (рис. а):

если в формуле (1) , то эллипс поляризации вырождается в отрезок прямой - линейная поляризация (рис. б):

Рис. Изображение круговой (а) и линейной (б) поляризаций электромагнитной волны.